Pytorch学习笔记（3）torch.autograd，逻辑回归模型训练

lesson5 torch.autograd

1. grad_tensors的使用

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)     # retain_grad()
b = torch.add(w, 1)

y0 = torch.mul(a, b)    # y0 = (x+w) * (w+1)    dy0/dw = 5
y1 = torch.add(a, b)    # y1 = (x+w) + (w+1)    dy1/dw = 2

loss = torch.cat([y0, y1], dim=0)       # [y0, y1]
grad_tensors = torch.tensor([1., 2.])  

loss.backward(gradient=grad_tensors)    # gradient 传入 torch.autograd.backward()中的grad_tensors

print(w.grad)  # 5*1+2*2 = 9

tensor([9.])

2. autograd.gard的使用

x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)     # y = x**2

grad_1 = torch.autograd.grad(y, x, create_graph=True)   # grad_1 = dy/dx = 2x = 2 * 3 = 6
print(type(grad_1))
print(grad_1)

grad_2 = torch.autograd.grad(grad_1[0], x)              # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
print(grad_2)x = torch.tensor([3.], requires_grad=True)
    y = torch.pow(x, 2)     # y = x**2

    grad_1 = torch.autograd.grad(y, x, create_graph=True)   # grad_1 = dy/dx = 2x = 2 * 3 = 6
    print(type(grad_1))
    print(grad_1)

    grad_2 = torch.autograd.grad(grad_1[0], x)              # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
    print(grad_2)

(tensor([6.], grad_fn=),)
(tensor([2.]),)

3. 梯度清零

梯度不清零的情况下：

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b)

    y.backward()
    print(w.grad,y.requires_grad)

tensor([5.]) True
tensor([10.]) True
tensor([15.]) True
tensor([20.]) True

梯度清零的情况下：

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b)

    y.backward()
    print(w.grad,y.requires_grad)

    w.grad.zero_()

tensor([5.]) True
tensor([5.]) True
tensor([5.]) True
tensor([5.]) True

4. requires_grad

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

print(a.requires_grad, b.requires_grad, y.requires_grad)

True True True

5.会报错的一个示例

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

w.add_(1)
"""
autograd小贴士：
    梯度不自动清零 
    依赖于叶子结点的结点，requires_grad默认为True     
    叶子结点不可执行in-place 
"""
y.backward()

RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

lesson5 逻辑回归模型训练

可能会有疑问的函数：

1. numpy.squeeze(a,axis = None)

a表示输入的数组；

axis用于指定需要删除的维度，但是指定的维度必须为单维度，否则将会报错

axis的取值可为None 或 int 或 tuple of ints, 可选。若axis为空，则删除所有单维度的条目；

举例：

import numpy as np
d=np.arange(10).reshape(5,1,2)
print(d.shape)  # (5,1,2)
b=np.squeeze(d)
print(np.squeeze(b).shape)

(5, 1, 2)
(5, 2)

或者也可以将axis设为1也是一样效果，但不能为0,2，因为只有1对应的是单维度

在torch的.squeeze()的用法举例：

import torch
a = torch.rand(4,1,3,2,1,5)

print(a.shape)
b = a.squeeze()
print(b.shape)

a1 = torch.rand(4,1,3,2,1,5)
print(a1.shape)
print(a1[0].shape)
c = a1[0].squeeze()
print(c.shape)
d = a1[1].squeeze()
print(d.shape)
e = a1[2].squeeze()
print(e.shape)

torch.Size([4, 1, 3, 2, 1, 5])
torch.Size([4, 3, 2, 5])
torch.Size([4, 1, 3, 2, 1, 5])
torch.Size([1, 3, 2, 1, 5])
torch.Size([3, 2, 5])
torch.Size([3, 2, 5])
torch.Size([3, 2, 5])

模型训练代码：

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)


# ============================ step 1/5 生成数据 ============================
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias      # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums)                         # 类别0 标签 shape=(100)
x1 = torch.normal(-mean_value * n_data, 1) + bias     # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums)                          # 类别1 标签 shape=(100)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)


# ============================ step 2/5 选择模型 ============================
class LR(nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x


lr_net = LR()   # 实例化逻辑回归模型


# ============================ step 3/5 选择损失函数 ============================
loss_fn = nn.BCELoss()

# ============================ step 4/5 选择优化器   ============================
lr = 0.01  # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)

# ============================ step 5/5 模型训练 ============================
for iteration in range(1000):

    # 前向传播
    y_pred = lr_net(train_x)

    # 计算 loss
    loss = loss_fn(y_pred.squeeze(), train_y)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()

    # 清空梯度
    optimizer.zero_grad()

    # 绘图
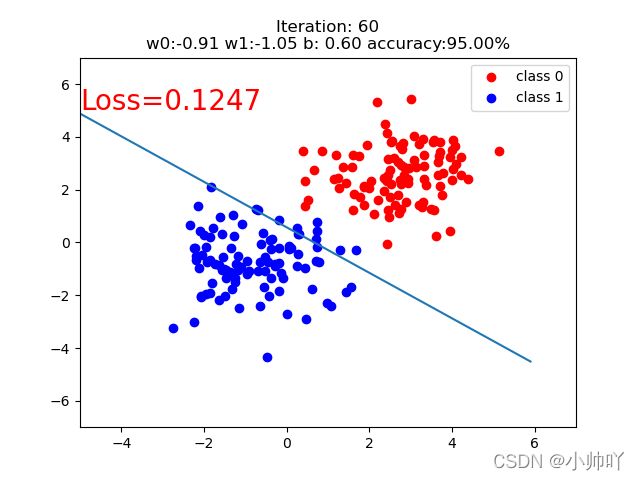
    if iteration % 20 == 0:

        mask = y_pred.ge(0.5).float().squeeze()  # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率

        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')

        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1

        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)

        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
        plt.legend()

        plt.show()
        plt.pause(0.5)

        if acc > 0.99:
            break

部分截图如下：