【自适应优化】如何利用麻雀优化算法(SSA)实现卷积神经网络(CNN)应对不同分类训练任务的参数/结构优化?(Matlab+Python)
目录
- 写作初衷
- 一、麻雀优化算法简介
- 二、优化流程
- 三、环境需求
- 四、关键模块(以Python为例)
-
- 1.定义麻雀优化算法(SSA.py)
- 2.待优化的CNN模块(model.py)
- 3.结构定义主函数(main.py)
- 五、结果展示
-
- 训练过程:
- 保存结果:
- 六、完整项目代码(Matlab+Python)
写作初衷
本文主要内容即介绍如何建立一种由麻雀优化算法(sparrow search algorithm,SSA)对简单的四层卷积神经网络(CNN)中(Python版18、Matlab版10)个参数或结构进行自适应优化的体系以应对不同的分类训练任务。
一、麻雀优化算法简介
麻雀优化算法(sparrow search algorithm,SSA)是受麻雀觅食行为和反捕食行为启发而提出的一种新型群体智能优化算法,在2020年提出,具体可抽象为发现者-追随者模型,并加入侦查预警机制。具体原理及代码可见链接。
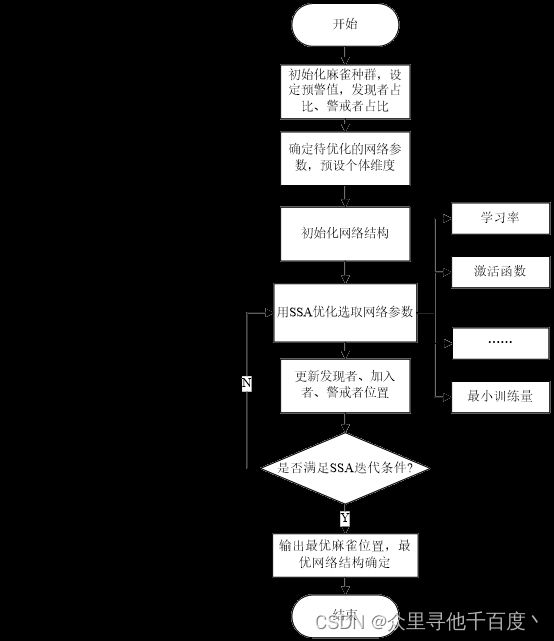
二、优化流程
利用麻雀优化算法对CNN中参数或结构进行自适应优化的总体流程如下图所示:
三、环境需求
Matlab版本所需环境:
- Deep Learning Toolbox
Python版本所需环境:
- Python 3.7
- pytorch 1.7.1
- CUDA+cuDNN
- numpy
- pandas
- scipy
四、关键模块(以Python为例)
1.定义麻雀优化算法(SSA.py)
部分功能代码:
import numpy as np
import random
import copy
import scipy.io
''' 种群初始化函数 '''
def initial(pop, dim, ub, lb,fun):
X = np.zeros([pop, dim])
x0 = random.random() # 初始点
for i in range(pop):
for j in range(dim):
X[i, j] = x0 * (ub[j] - lb[j]) + lb[j]
if X[i, j] > ub[j]:
X[i, j] = ub[j]
if X[i, j] < lb[j]:
X[i, j] = lb[j]
return X, lb, ub
'''边界检查函数'''
def BorderCheck(X,ub,lb,pop,dim):
for i in range(pop):
for j in range(dim):
if X[i,j]>ub[j]:
X[i,j] = ub[j]
elif X[i,j]<lb[j]:
X[i,j] = lb[j]
return X
'''计算适应度函数'''
def CaculateFitness(X,fun):
pop = X.shape[0]
fitness = np.zeros([pop, 1])
for i in range(pop):
fitness[i] = fun(X[i, :])
return fitness
'''麻雀发现者更新'''
def PDUpdate(X,PDNumber,ST,Max_iter,dim):
X_new = copy.copy(X)
R2 = random.random()
for j in range(PDNumber):
if R2<ST:
X_new[j,:] = X[j,:]*np.exp(-j/(random.random()*Max_iter))
else:
X_new[j,:] = X[j,:] + np.random.randn()*np.ones([1,dim])
return X_new
'''麻雀加入者更新'''
def JDUpdate(X,PDNumber,pop,dim):
X_new = copy.copy(X)
for j in range(PDNumber+1,pop):
if j>(pop - PDNumber)/2 + PDNumber:
X_new[j,:]= np.random.randn()*np.exp((X[-1,:] - X[j,:])/j**2)
else:
#产生-1,1的随机数
A = np.ones([dim,1])
for a in range(dim):
if(random.random()>0.5):
A[a]=-1
AA = np.dot(A,np.linalg.inv(np.dot(A.T,A)))
X_new[j,:]= X[1,:] + np.abs(X[j,:] - X[1,:])*AA.T
return X_new
'''麻雀搜索算法'''
def SSA(pop,dim,lb,ub,Max_iter,fun):
ST = 0.6 #预警值
PD = 0.7 #发现者的比列,剩下的是加入者
SD = 0.3 #意识到有危险麻雀的比重
PDNumber = int(pop*PD) #发现者数量
SDNumber = int(pop*SD) #意识到有危险麻雀数量
X,lb,ub = initial(pop, dim, ub, lb,fun) #初始化种群
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
GbestScore = copy.copy(fitness[0])
GbestPositon = np.zeros([1,dim])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve = np.zeros([Max_iter,1])
for i in range(Max_iter):
BestF = fitness[0]
X = PDUpdate(X,PDNumber,ST,Max_iter,dim)#发现者更新
X = JDUpdate(X,PDNumber,pop,dim) #加入者更新
X = SDUpdate(X,pop,SDNumber,fitness,BestF) #危险更新
X = BorderCheck(X,ub,lb,pop,dim) #边界检测
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
if(fitness[0]<=GbestScore): #更新全局最优
GbestScore = copy.copy(fitness[0])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve[i] = GbestScore
return GbestScore,GbestPositon,Curve
2.待优化的CNN模块(model.py)
部分功能代码:
import torch.nn as nn
import torch
import sys
import math
class model_4l(nn.Module):
def __init__(self, num_classes=1000, init_weights=False):
super(model_4l, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, Conv1, kernel_size=Conv_k_1, stride=3, padding=2),
CA_fun_1(),
# nn.ReLU(inplace=True),
# nn.Sigmoid(),
# nn.ReLU6(inplace=True),
# nn.Tanh(),
# nn.LeakyReLU(),
# nn.Softsign(),
# nn.ELU(),
# nn.MaxPool2d(kernel_size=3, stride=2),
# nn.AvgPool2d(kernel_size=3, stride=2),
Con_pool_1(),
nn.Conv2d(Conv1, Conv2, kernel_size=Conv_k_2, stride=1, padding=2),
CA_fun_2(),
Con_pool_2(),
# nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(Conv2, Conv3, kernel_size=Conv_k_3, stride=1, padding=1),
nn.Conv2d(Conv3,Conv4, kernel_size=Conv_k_4, stride=1, padding=1),
CA_fun_4(),
Con_pool_3(),
)
Fea1 = math.floor(((224 + 4 - Conv_k_1) / 3) + 1)
Fea1_pool = math.floor(((Fea1 - 3) / 2) + 1)
Fea2 = math.floor((Fea1_pool + 4 - Conv_k_2) + 1)
Fea2_pool = math.floor(((Fea2 - 3) / 2) + 1)
Fea3 = math.floor((Fea2_pool + 2 - Conv_k_3) + 1)
Fea4 = math.floor((Fea3 + 2 - Conv_k_4) + 1)
Fea4_pool = math.floor(((Fea4 - 3) / 2) + 1)
self.classifier = nn.Sequential(
nn.Dropout(p=0.5),
nn.Linear(Conv4 * Fea4_pool * Fea4_pool, 100),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(100, 50),
nn.ReLU(inplace=True),
nn.Linear(50, num_classes),
)
if init_weights:
self._initialize_weights()
def forward(self, x):
x = self.features(x)
x = torch.flatten(x, start_dim=1)
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
3.结构定义主函数(main.py)
| 待优化的18个结构/参数明细 |
|---|
| 四层卷积核通道数 |
| 批次大小 |
| 学习率 |
| 四层激活函数 |
| 三层池化方式 |
| 优化器选取 |
| 卷积核尺寸 |
部分功能代码:
import numpy as np
from matplotlib import pyplot as plt
import Tent_back_SSA
import os
import scipy.io
'''定义目标函数'''
def fun_cnn(X):
X = X[:]
X = X.tolist()
os.system('python train.py {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} '.format(X[0],X[1],X[2],X[3],X[4],X[5],X[6],X[7],X[8],X[9],X[10],X[11],X[12],X[13],X[14],X[15],X[16],X[17]))
data = scipy.io.loadmat('./Curw_best_value/best_acc.mat')
O = 1-data['acc'][:, 0]
return O
'''主函数 '''
#设置参数
pop = 20 #种群数量
MaxIter = 5 #最大迭代次数
dim = 18 #维度
lb = np.zeros((dim,1))
ub = np.zeros((dim,1))
lb[0] = 3.1*np.ones([1, 1]) #卷积核1通道数下边界
ub[0] = 15.9*np.ones([1, 1])#上边界
lb[1] = 15.1*np.ones([1, 1]) #卷积核2通道数下边界
ub[1] = 30.9*np.ones([1, 1])#上边界
lb[2] = 30.1*np.ones([1, 1]) #卷积核3通道数下边界
ub[2] = 45.9*np.ones([1, 1])#上边界
lb[3] = 45.1*np.ones([1, 1]) #卷积核4通道数下边界
ub[3] = 60.9*np.ones([1, 1])#上边界
lb[4] = 16.1*np.ones([1, 1]) #批次大小下边界
ub[4] = 64.9*np.ones([1, 1])#上边界
lb[5] = 0.00001*np.ones([1, 1]) #学习率下边界(无需赋整)
ub[5] = 0.1*np.ones([1, 1])#上边界
lb[6] = 1*np.ones([1, 1]) #卷积核1激活函数下边界(1-70 7个区间)
ub[6] = 70*np.ones([1, 1])#上边界
lb[7] = 1*np.ones([1, 1]) #卷积核2激活函数下边界(同上)
ub[7] = 70*np.ones([1, 1])#上边界
lb[8] = 1*np.ones([1, 1]) #卷积核3激活函数下边界(同上)
ub[8] = 70*np.ones([1, 1])#上边界
lb[9] = 1*np.ones([1, 1]) #卷积核4激活函数下边界(同上)
ub[9] = 70*np.ones([1, 1])#上边界
lb[10] = 1*np.ones([1, 1]) #卷积核1池化方式下边界(1-20 2个区间)
ub[10] = 20*np.ones([1, 1])#上边界
lb[11] = 1*np.ones([1, 1]) #卷积核2池化方式下边界(1-20 2个区间)
ub[11] = 20*np.ones([1, 1])#上边界
lb[12] = 1*np.ones([1, 1]) #卷积核4池化方式下边界(1-20 2个区间)
ub[12] = 20*np.ones([1, 1])#上边界
lb[13] = 1*np.ones([1, 1]) #优化器选择(1-80 8个区间)
ub[13] = 80*np.ones([1, 1])#上边界
lb[15] = 30*np.ones([1, 1]) #卷积核2尺寸(30-70 4个区间)
ub[15] = 70*np.ones([1, 1])#上边界
lb[16] = 30*np.ones([1, 1]) #卷积核3尺寸(30-70 4个区间)
ub[16] = 70*np.ones([1, 1])#上边界
lb[17] = 20*np.ones([1, 1]) #卷积核4尺寸(20-60 4个区间)
ub[17] = 60*np.ones([1, 1])#上边界
#适应度函数选择
fobj = fun_cnn
GbestScore,GbestPositon,Curve = Tent_back_SSA.Te_Back_SSA(pop,dim,lb,ub,MaxIter,fobj)
print('最优适应度值:',1-GbestScore)
print('最优解:',GbestPositon)
#绘制适应度曲线
plt.figure(1)
plt.plot(100*(1-Curve),'r-',linewidth=2)
plt.xlabel('Iteration',fontsize='medium')
plt.ylabel("Fitness",fontsize='medium')
plt.grid()
plt.title('SSA',fontsize='large')
plt.show()
五、结果展示
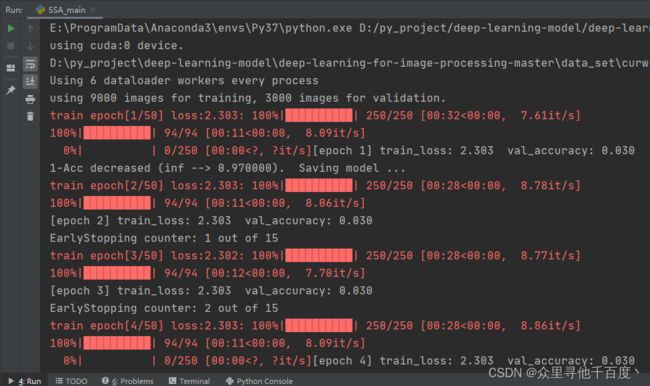
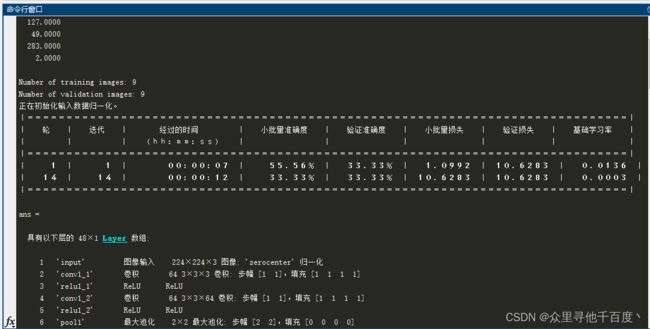
训练过程:
Python:设置有早停机制,当模型迭代精度在15轮后未有提升,则停止优化算法中本回合迭代取本回合最优结果。
保存结果:
PS:将麻雀搜索算法中每轮种群值、最优种群,每轮最优值以及最优搭配下预训练模型进行保存,方便后续数据处理。


六、完整项目代码(Matlab+Python)
由于项目代码较多,文章内供学习的代码示例仅提供了Python版本的部分内容,完整Python版以及Matlab版项目请点击下方链接自行下载。使用过程若有任何问题请私信作者,或联系Q:1518686357。
Matlab版本:https://mianbaoduo.com/o/bread/Yp2ZlJdq
Python版本:https://mianbaoduo.com/o/bread/Yp2Zk59x