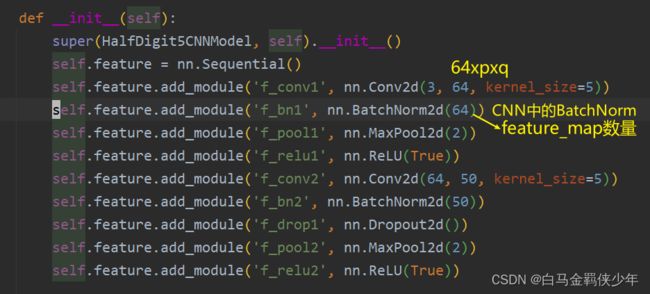
深入理解BatchNorm的原理、代码实现以及BN在CNN中的应用

深入理解BatchNorm的原理、代码实现以及BN在CNN中的应用

BatchNorm是算法岗面试中几乎必考题，本文将带你理解BatchNorm的原理和代码实现，以及详细介绍BatchNorm在CNN中的应用。NLP中常见的LayerNorm的解读，详见我的另一篇博客深入理解NLP中LayerNorm的原理以及LN的代码详解

一、BatchNorm论文

论文题目：Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift
论文地址：https://arxiv.org/pdf/1502.03167.pdf

BatchNorm伪代码如下：

1.2 问题：为什么在Normalize后还要将$x$复原成$y$？

答：因为我们这里做的是标准化，但是可能真正训练的时候还是方差大一点，或者均值比0大一些比较好的话，那么这里允许你还原回去，至于还原成什么样，神经网络会自己找出好的均值和方差（$\gamma$和$\beta$都是可学习参数）李沐 09:40

二、BatchNorm代码

$$\mathrm{y}=\frac{x-\mathrm{mean}(x)}{\sqrt{\mathrm{Var}(x)}+eps}\ast \mathrm{gamma}+\mathrm{beta}$$
根据数据维度的不同，PyTorch中的BatchNorm有不同的形式：

2.1 torch.nn.BatchNorm1d

官方文档：torch.nn.BatchNorm1d
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

• 2D input: (mini_batch, num_feature)，常见的结构化数据，如，房价预测问题中x的特征数有100个，torch.nn.BatchNorm1d(100)
• 3D input: (mini_batch, num_feature, additional_channel)，使用时 torch.nn.BatchNorm1d(num_feature)，不过这种维度一般不常用

2.2 torch.nn.BatchNorm2d

官方文档：torch.nn.BatchNorm2d
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

• 4D input: (mini_batch, num_feature_map, p, q)，常用于CV的图像数据，如CIFAR10（3x32x32），torch.nn.BatchNorm2d(3)

2.3 BatchNorm层的参数γ,β和统计量

Batch Norm层有可学习的参数γ和β，以及统计量running mean和running var

• （可学习参数）γ : weight of BatchNorm
• （可学习参数）β : bias of BatchNorm
• （统计量）running mean: 预测阶段会使用这个均值
• （统计量）running var: 预测阶段会使用这个方差

默认初始化参数$\gamma$和$\beta$ 为1和0

pytorch中用state_dict()可以查看上面这些信息

print("--- 4D:(mini_batch, num_feature, p, q) ---")
m = nn.BatchNorm2d(3, momentum=0.1)  # 例如, CIFAR10数据集是三通道的，3x32x32
print(m.state_dict().keys())
# 输出：odict_keys(['weight', 'bias', 'running_mean', 'running_var', 'num_batches_tracked'])

2.3.1 train模式

在pytorch中可以使用model.train()将BatchNorm层切换到train模式。

在train模式下参数γ和β会随着网络的反向传播进行梯度更新，而统计量running mean和running var则会用一种特定的方式进行更新。在Pytorch中的更新方式如下：

${\hat{x}}_{\text{new }}=(1-$ momentum $)\times \hat{x}+$ momentum $\times x_t$

• $\hat{x}$: running mean or running variance
• $x_t$: input mean and variance（训练时的第t个batch的均值和方差）
• 默认momentum为0.1

2.3.2 eval模式

在pytorch中可以使用model.eval()将BatchNorm层切换到eval模式。

在eval模式下，我们的模型不可能再等到预测的样本数量达到一个batch时，再进行归一化，而是直接使用train模式得到的统计量running mean和running var进行归一化。

2.4 代码：Pytorch实战演练

import torch
import torch.nn as nn

bs = 64

print("Pytorch Batch Norm Layer详解")
print("--- 2D input:(mini_batch, num_feature) ---")
# With Learnable Parameters
m = nn.BatchNorm1d(400)  # 例如，房价预测：x的特征数是400，y是房价
# Without Learnable Parameters（无学习参数γ和β）
# m = nn.BatchNorm1d(100, affine=False)
inputs = torch.randn(bs, 400)
print(m(inputs).shape)


print("Batch Norm层的γ和β是要训练学习的参数")
print("γ:", m.state_dict()['weight'].shape)  # gammar
print("β:", m.state_dict()['bias'].shape)  # beta
print("")


print("--- 3D input:(mini_batch, num_feature, other_channel) ---")
m = nn.BatchNorm1d(32)
inputs = torch.randn(bs, 32, 32)  # 这种格式的数据不常用
print(m(inputs).shape)

print("Batch Norm层的γ和β是要训练学习的参数")
print("γ:", m.state_dict()['weight'].shape)  # gammar
print("β:", m.state_dict()['bias'].shape)  # beta
print("")


print("--- 4D input:(mini_batch, num_feature, H, W) ---")
m = nn.BatchNorm2d(3)  # 例如, CIFAR10数据集是三通道的，3x32x32

inputs = torch.randn(bs, 3, 32, 32)
print(m(inputs).shape)

print("Batch Norm层的γ和β是要训练学习的参数")
print("γ:", m.state_dict()['weight'].shape)  # gammar
print("β:", m.state_dict()['bias'].shape)  # beta
print("Batch Norm层的running_mean和running_var是统计量（主要用于预测阶段）")
print("running_mean:", m.state_dict()['running_mean'].shape)
print("running_var:", m.state_dict()['running_var'].shape)

输出：

Pytorch Batch Norm Layer详解
--- 2D input:(mini_batch, num_feature) ---
torch.Size([64, 400])
Batch Norm层的γ和β是要训练学习的参数
γ: torch.Size([400])
β: torch.Size([400])

--- 3D input:(mini_batch, num_feature, other_channel) ---
torch.Size([64, 32, 32])
Batch Norm层的γ和β是要训练学习的参数
γ: torch.Size([32])
β: torch.Size([32])

--- 4D input:(mini_batch, num_feature, H, W) ---
torch.Size([64, 3, 32, 32])
Batch Norm层的γ和β是要训练学习的参数
γ: torch.Size([3])
β: torch.Size([3])
Batch Norm层的running_mean和running_var是统计量（主要用于预测阶段）
running_mean: torch.Size([3])
running_var: torch.Size([3])

三、BatchNorm在CNN中的应用

我们在第二部分的代码中发现，BatchNorm2d的参数γ和β数量是跟特征图的数量是一致的，并不是我们直观认为的num_feature*H*W个参数，这是为什么呢？

《百面机器学习》P221是这样解释的：
BatchNorm批量归一化在卷积神经网络中应用时，需要注意卷积神经网络的参数共享机制。每一个卷积核的参数在不同位置的神经元当中是共享的，因此同一个特征图的所有神经元也应该被一起归一化！

• 换句话说就是，你一个特征图用的是共享的卷积核参数，所以这个特征图中的每个神经元(共H*W个)也应该共享参数$\gamma ,\beta$。如果有$f$个卷积核，就对应$f$个特征图和$f$组不同的$\gamma$和$\beta$参数

下面的解释来自hjimce

• 假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有6*100*100个神经元，如果采用BN，就会有6*100*100个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。
• 卷积神经网络经过卷积后得到的是一系列的特征图，如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,f,p,q)，m为min-batch sizes，f为特征图个数，p、q分别为特征图的宽高。在cnn中我们可以把每个特征图看成是一个特征处理，因此在使用Batch Normalization，mini-batch size 的大小相当于m*p*q，于是对于每个特征图都只有一对可学习参数：γ、β。

3.1 图解：卷积神经网络中的BatchNorm

这里我特意画了一个图来让大家看清楚CNN中Batchnorm到底是怎么做的

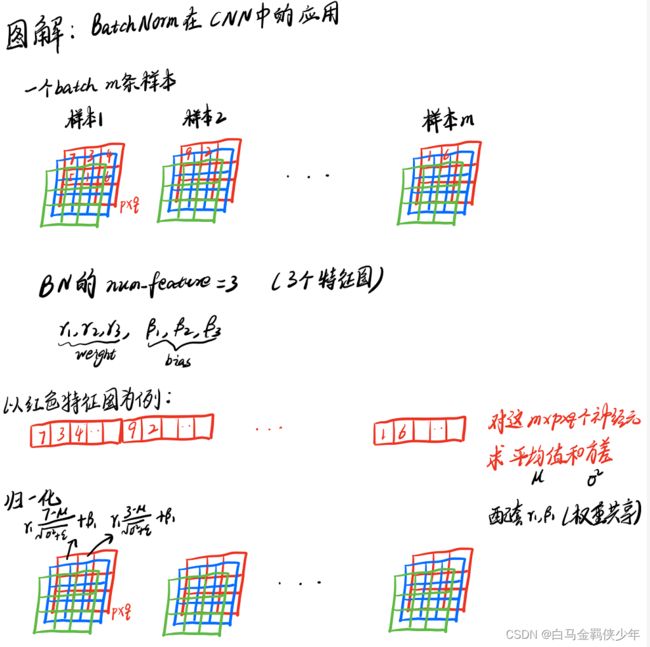
总结来说：

1. 对于某个特征图而言，一个batch共有m个这样的特征图，并且每个特征图有p*q个神经元，把所有的m*p*q个神经元拉直，然后求得平均值和方差。
2. 对m个这样特征图的p*q个神经元的每个神经元，利用求出的平均值和方差做下数据变换。

参考资料：BN的操作流程

---

3.2 BatchNorm torch代码实现

https://d2l.ai/chapter_convolutional-modern/batch-norm.html

import torch
from torch import nn
from d2l import torch as d2l


def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # Use `is_grad_enabled` to determine whether the current mode is training
    # mode or prediction mode
    if not torch.is_grad_enabled():
        # If it is prediction mode, directly use the mean and variance
        # obtained by moving average
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # When using a fully-connected layer, calculate the mean and
            # variance on the feature dimension
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # When using a two-dimensional convolutional layer, calculate the
            # mean and variance on the channel dimension (axis=1). Here we
            # need to maintain the shape of `X`, so that the broadcasting
            # operation can be carried out later
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # In training mode, the current mean and variance are used for the
        # standardization
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # Update the mean and variance using moving average
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # Scale and shift
    return Y, moving_mean.data, moving_var.data

下面是来自于Keras卷积层的BN实现的一小段主要源码：

# Keras BatchNorm
input_shape = self.input_shape
reduction_axes = list(range(len(input_shape)))
del reduction_axes[self.axis]
broadcast_shape = [1] * len(input_shape)
broadcast_shape[self.axis] = input_shape[self.axis]
if train:
    m = K.mean(X, axis=reduction_axes)
    brodcast_m = K.reshape(m, broadcast_shape)
    std = K.mean(K.square(X - brodcast_m) + self.epsilon, axis=reduction_axes)
    std = K.sqrt(std)
    brodcast_std = K.reshape(std, broadcast_shape)
    mean_update = self.momentum * self.running_mean + (1-self.momentum) * m
    std_update = self.momentum * self.running_std + (1-self.momentum) * std
    self.updates = [(self.running_mean, mean_update),
                    (self.running_std, std_update)]
    X_normed = (X - brodcast_m) / (brodcast_std + self.epsilon)
else:
    brodcast_m = K.reshape(self.running_mean, broadcast_shape)
    brodcast_std = K.reshape(self.running_std, broadcast_shape)
    X_normed = ((X - brodcast_m) /
                (brodcast_std + self.epsilon))
out = K.reshape(self.gamma, broadcast_shape) * X_normed + K.reshape(self.beta, broadcast_shape)

附：pytorch中取mean的操作

import torch

bs = 64
a = torch.randn(bs, 100, 32, 28)
# 将轴0,2,3的元素都放在一起取平均值
print(torch.mean(a, axis=(0, 2, 3)).shape)  # torch.Size([100])

附：CNN网络中的BatchNorm2d

四、BatchNorm的优缺点

BN的优点：

• 解决内部协变量偏移，简单来说训练过程中，各层分布不同，增大了学习难度，BN缓解了这个问题。当然后来也有论文证明BN有作用和这个没关系，而是可以使损失平面更加的平滑，从而加快收敛速度。
• 缓解了梯度饱和问题（如果使用sigmoid这种含有饱和区间的激活函数的话），加快收敛。

BN的缺点

• Batch size比较小的时候，效果会比较差。因为他是用一个batch中的均值和方差来模拟全部数据的均值和方差。比如你一个batch只有2个样本，那你两个样本的均值和方差就不能很好地代表全班人的均值和方差，所以效果肯定就不好。
• BN是计算机视觉CV的标配，但在自然语音处理NLP中效果一般较差，取而代之的是LN。关于LayerNorm的详解，可以参考我另一篇博客：深入理解NLP中LayerNorm的原理以及LN的代码详解

五、BatchNorm反向传播公式推导

详见我的Notion笔记

六、参考资料

[1] 李宏毅2021机器学习 第5节 Batch Normalization（学习笔记）
[2] 深度学习（二十九）Batch Normalization 学习笔记 （讲得挺全面的）
[3] BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm简介（不同Norm的对比）
[4] BatchNorm behaves different in train() and eval() #5406
[5] BatchNorm2d原理、作用及其pytorch中BatchNorm2d函数的参数讲解
[6] 神经网络之BN层
[7] 5 分钟理解 BatchNorm
[8] Pytorch的BatchNorm层使用中容易出现的问题
[9] 【深度学习】深入理解Batch Normalization批标准化
[10] BN踩坑记–谈一下Batch Normalization的优缺点和适用场景
[11] 深度神经网络架构【斯坦福21秋季：实用机器学习中文版】