py实现高斯列选主元消元法

什么是高斯列选主元消元法

高斯消元法解决的问题是线性方程组的求解问题。
比如下面这个方程组
x+2y = 3
x+4y = 8
我们大学之前学习的方法其实就是高斯消元法。
上面的方程组我们还可以写成矩阵的乘积形式：
$$\left[\begin{array}{cc}1& 2\\ 1& 4\end{array}\right]\ast \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}3\\ 8\end{array}\right]$$

就这样，我们可以将上述表达式写成Ax = b的形式，其中A一定是一个方阵。
只要A是一个非奇异的矩阵，我们就能求出方程组的唯一解。

将之前的方法总结成规律，其实就是我们将一个n阶矩阵变成n-1阶矩阵的过程。
说起来可能有一点绕。
拿一个四阶矩阵举例吧：
$$\left[\begin{array}{cccc}a& b& c& d\\ f& g& h& i\\ k& l& m& n\\ p& q& r& s\end{array}\right]$$
我们是能做到使用矩阵行的加减法，对于第二行减去 (f/a)倍的第一行，这样就能使A[2][1]为0。
对三四行的操作同理，这样我们的第一列除了第一行的元素，剩下的都是0，这样我们就只需要对下面得到3阶矩阵进行处理即可。
$$\left[\begin{array}{ccc}{g}^{\prime }& h^{\prime }& i^{\prime }\\ l^{\prime }& m^{\prime }& n^{\prime }\\ q^{\prime }& r^{\prime }& s^{\prime }\end{array}\right]$$
处理的过程中，我们实际上还需要同时对b矩阵进行处理！
（这个过程其实就是我们之前学习的消元过程）

最终，我们得到的A’阵实际上是一个上三角矩阵，对于最后一行来说，除了A[n][n]’，剩下的都是0，所以有A[n][n]’ *x = b[n]’，直接使用除法解决问题。
对于倒数第二行，有A[n-1][n-1]’*x[n-1] + A[n-1][n]*x[n] = b[n-1]，但是我们已经知道了x[n]，剩下的事都可以解决。
对于剩下的x[i]都是同理，只需要从x[n]倒着计算回去就行了。

上述的过程，就是高斯消元法的消元过程和回代过程。

接下来是列选主元的问题。
如果说在一列中，如果有的元素绝对值很大，而我们选择的除数很小，则会造成误差，所以我们提出了列选主元的方法。
（这个具体的还是自己去查查，我也说不太清楚，毕竟上课老摸鱼了）
列选主元的原因是a太小，f太大，所以我们就将f行移动到a行上去。

比如下图中在处理A[2][2]到A[n][n]时，我们发现3/2的绝对值是最大的，所以我们和-1交换
这里注意一下，交换的同时b矩阵也需要交换，所以有时候其实是写成(A|B)的形式，能减少我们忘记的概率。

实现

用process on画了一个流程图，实验报告要的，不然直接截指导书的图了（doge

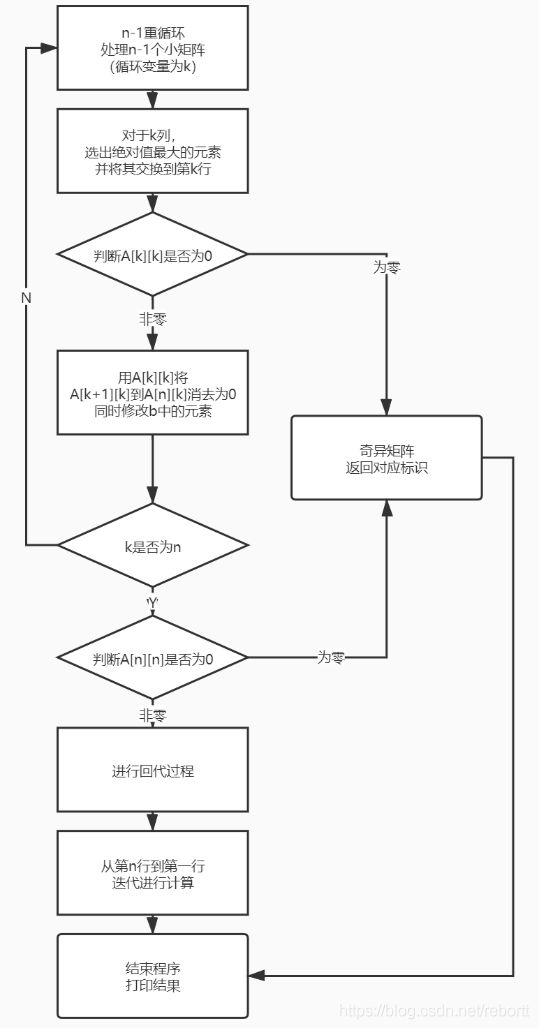
只不过我们添加了两个判断奇异矩阵的地方。
一个是选好列主元时，如果绝对值最大的还是0，说明一整列都是0，直接没法消元了好叭，绝对奇异矩阵了；
另一个是我们的A[n][n]，如果是零，那还求个鬼。

上代码：
修改部分：

1. 每一次只需要修改一下n的值，也就是矩阵的阶数
2. 填入A、b即可

另外别忘了py数组（列表）是从零开始的

n = 4
x = [0]*n
A = [
    [136.01, 90.860, 0, 0],
    [90.860, 98.810, -67.590, 0],
    [0, -67.590, 132.01, 46.260],
    [0, 0, 46.260, 177.17]
]
b = [226.87, 122.08, 110.68, 223.43]
def Gauss(n, A, b):
    global x
    for k in range(0, n-1):
    	# 找每一列主元，最开始我们选k行k列的为最大
        the_max = abs(A[k][k])	#最大元值
        the_max_p = k			#最大元列的下标
        for p in range(k+1, n):
            if abs(A[p][k]) > the_max:
                the_max = abs(A[p][k])
                the_max_p = p
        if A[the_max_p][k] == 0:
        	#最大元为0，奇异
            return -1
        elif the_max_p != k:
        	#需要交换两行
            temp = A[the_max_p]
            A[the_max_p] = A[k]
            A[k] = temp
            #之前忘了换b，坑得老惨了
            temp = b[k]
            b[k] = b[the_max_p]
            b[the_max_p] = temp
        #消去公式，直接照抄就行
        for i in range(k+1, n):
            for j in range(k+1, n):
                A[i][j] -= A[k][j]*A[i][k]/A[k][k]
            b[i] -= b[k]*A[i][k]/A[k][k]
	#奇异矩阵
    if A[n-1][n-1] == 0:
        return -1
    # 回代，这部分还是套公式
    x[n-1] = b[n-1]/A[n-1][n-1]
    for k in range(n-2, -1, -1):
        get_sum = 0
        for j in range(k+1, n):
            get_sum += A[k][j]*x[j]
        x[k] = b[k]-get_sum
        x[k] /= A[k][k]
    return 0

ret = Gauss(n, A, b)
if ret != -1:
    print(x)