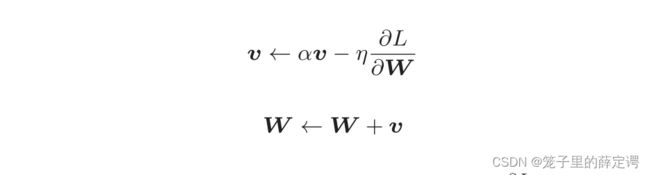NNDL 作业11：优化算法比较

目录

1. 编程实现下式，并观察特征

2.观察梯度方向

3. 编写代码实现算法，并可视化轨迹

4. 分析上图，说明原理

1.为什么SGD会走“之字形”？其它算法为什么会比较平滑？ 

2.Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

3.仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

4.四种方法分别用了多长时间？是否符合预期？

5.调整学习率、动量等超参数，轨迹有哪些变化？

5. Adam这么好，SGD是不是就用不到了？

6. 在SGD、Momentum、AdaGrad、Adam的基础上，增加RMSprop、Nesterov算法，全面总结它们的优缺点

总结

参考链接

---

1. 编程实现下式，并观察特征
 

 

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def func(x, y):
    return x * x / 20 + y * y


def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数

    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)

    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')

    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()


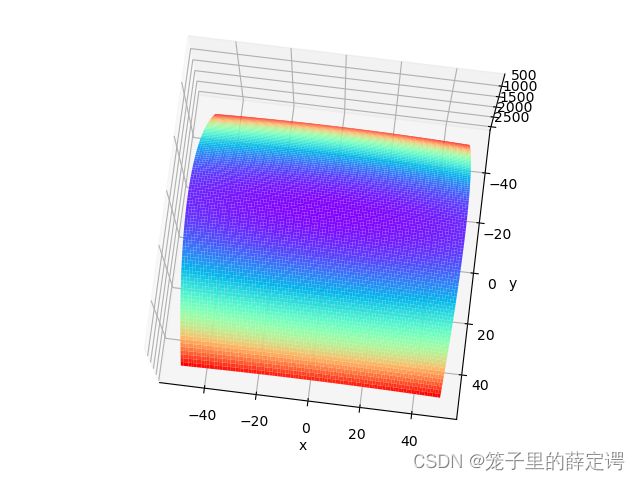
paint_loss_func()

 

 特征：有全局最小值、是一个向x轴方向延申的“碗”状函数

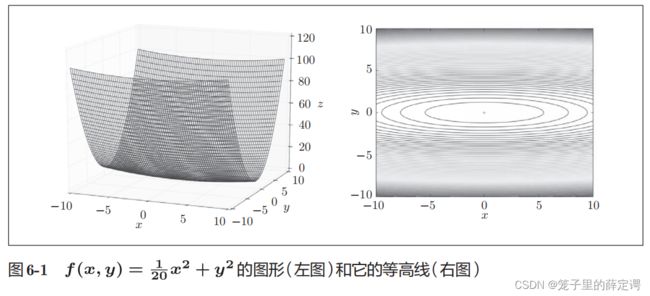
下图为鱼书给出的等高线图： 等高线呈向x轴方向延伸的椭圆状 

2.观察梯度方向

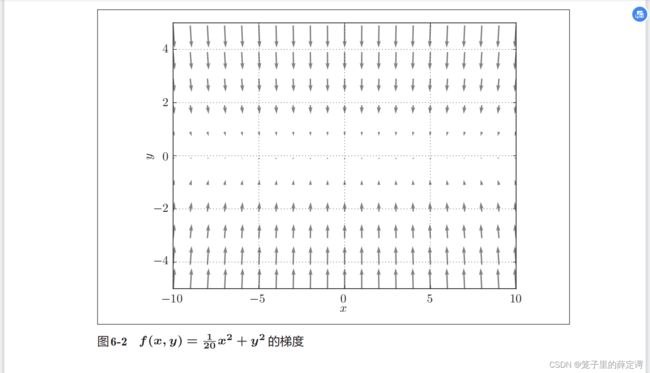
 特征：Y轴方向梯度大，X轴方向梯度小；很多位置的梯度并没有指向最小位置(0,0)

3. 编写代码实现算法，并可视化轨迹

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


class Momentum:
    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]


class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]


class AdaGrad:
    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:
    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)


def f(x, y):
    return x ** 2 / 20.0 + y ** 2


def df(x, y):
    return x / 10.0, 2.0 * y


init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
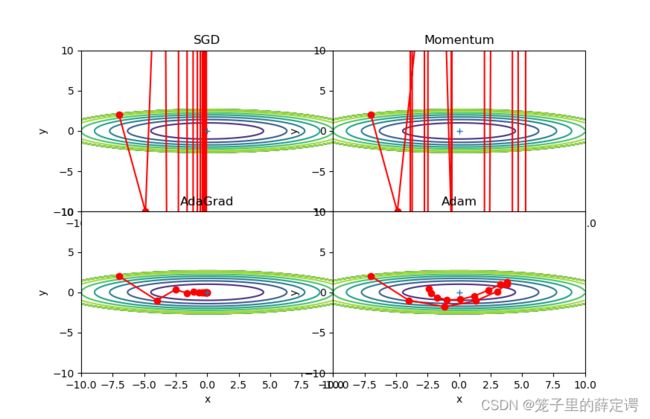
plt.show()

 从可视化结果来看，收敛效果排序依次为AdaGrad、Adam、Momentum、SGD。

4. 分析上图，说明原理

1.为什么SGD会走“之字形”？其它算法为什么会比较平滑？ 

因为在此函数中梯度的方向并没有指向最小值的方向，SGD只是单纯的朝着梯度方向，放弃了对梯度准确性的追求，会使得其在 函数的形状非均向(比如y方向变化很大时，x方向变化很小 )，能迂回往复地寻找，效率很低。

其它算法为什么会比较平滑下文解释。

2.Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

SGD形式：

 Momentum形式：

新出现了一个变量v，对应物理上的速度。表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加。

体现在图上为：“之”字形的“程度”减轻。

这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱“之”字形的变动程度。(摘自鱼书P169)。
 

AdaGrad形式：

注：AdaGrad会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境地学习，更新量就会变为 0，完全不再更新。

体现在图上为:函数的取值高效地向着最小值移动。
这是因为y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之”字形的变动程度有所衰减。(摘自鱼书P172)

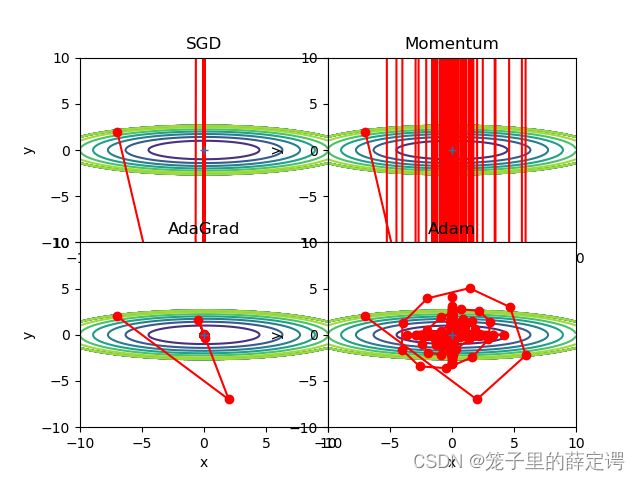
3.仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

轨迹上来看，是这样，因为此时Adam和AdaGrad的学习率并不相同，并且Adam和AdaGrad选择的均是一个恰当的学习率。我将他俩调到一个相同且不适合的学习率，结果如下：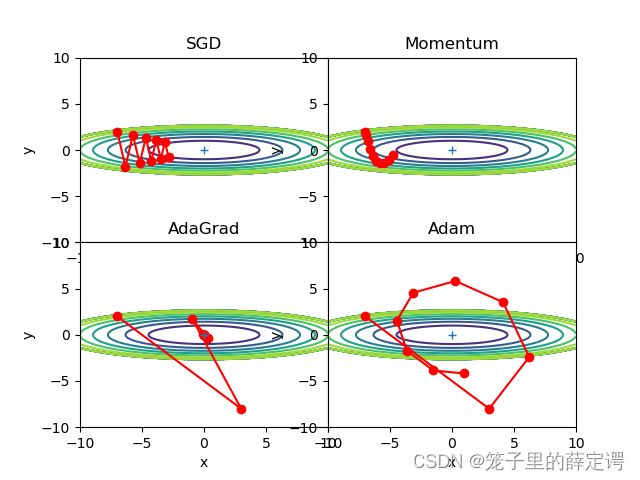

可以发现，AdaGrad的效果仍好于Adam。
 

4.四种方法分别用了多长时间？是否符合预期？

将原来搜索点增加到10000，进而比较四种算法的时间优劣，运行结果如下:

 符合预期，因为由公式编写出来的参考代码全都是手撸而不是框架包装好的，这四种方法参数计算的复杂程度逐渐增加，所以与之对应的计算时间就会增加。

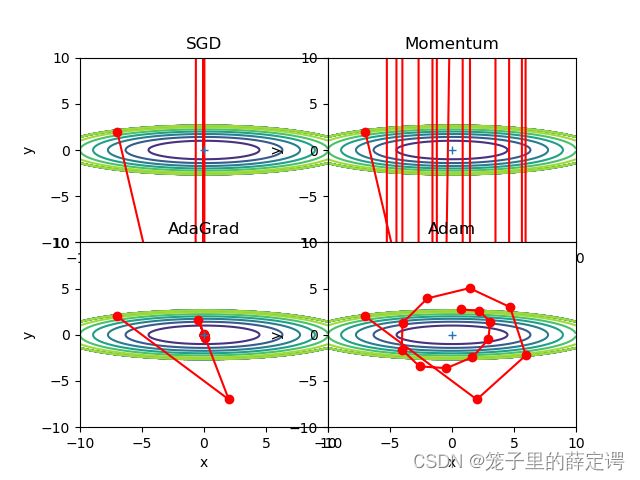
5.调整学习率、动量等超参数，轨迹有哪些变化？

方便对比效果，我将他们调节到一致：

lr=0.09，迭代搜索15次和15000次：

lr=0.9，迭代搜索15次：

 

 lr=3，迭代搜索15次和15000次：

 

  lr=9，迭代搜索15次和15000次：

 

 从以上对比实验的路径可以发现，对于本例，SGD和Momentum很容易错过全局最小值，Adam需要较长的时间和较多的搜索次数来找到全局最小值，AdaGrad效果最好。

5. Adam这么好，SGD是不是就用不到了？

https://arxiv.org/pdf/1705.08292.pdf 论文中提到

Despite the fact that our experimental evidence demonstrates that adaptive methods are not advantageous for machine learning, the Adam algorithm remains incredibly popular. We are not sure exactly as to why ……

大致意思是：尽管我们的实验证据表明自适应方法对机器学习不利，但Adam算法仍然非常受欢迎。我们不确定为什么......

优化过程：

SGD： 将其代入，可得下降梯度：
Momentum：
AdaGrad：SGD及其变种以同样的学习率更新每个参数，但深度神经网络往往包含大量的参数，这些参数并不是总会用得到（想想大规模的embedding）。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。
所以就使用二阶动量——该维度上，迄今为止所有梯度值的平方和：

去更新历史频率，此时的下降梯度变为，也就是如今优化算法最常见的形式。
 Adam：

 

上述各大优化算法的学习率为：

其中，SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这两类算法会使得学习率不断递减，最终收敛到0，模型也得以收敛。

但Adam不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得 可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛，也就是它的第一个缺点。

第二个缺点：同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。https://arxiv.org/abs/1705.08292该文通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。同样地，

Improving Generalization Performance by Switching from Adam to SGD，进行了实验验证。他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

于是该文提出了一个用来改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错。

网上的佬给出这样一句话：算法固然美好，数据才是根本。
该佬根据怒怼Adam的paper，提出多数都构造了一些比较极端的例子来演示了Adam失效的可能性。这些例子一般过于极端，实际情况中可能未必会这样，但这提醒了我们，理解数据对于设计算法的必要性。优化算法的演变历史，都是基于对数据的某种假设而进行的优化，那么某种算法是否有效，就要看你的数据是否符合该算法的胃口了。

并且其总结为：Adam之流虽然说已经简化了调参，但是并没有一劳永逸地解决问题，默认参数虽然好，但也不是放之四海而皆准。因此，在充分理解数据的基础上，依然需要根据数据特性、算法特性进行充分的调参实验，找到自己炼丹的最优解。而这个时候，不论是Adam，还是SGD，都已经不重要了。

非常建议去看一下该佬关于主流优化算法的对比讲解以及网络结构优化调参的tricks:
一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎

Adam那么棒，为什么还对SGD念念不忘 (2)—— Adam的两宗罪 - 知乎

Adam那么棒，为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略 - 知乎

6. 在SGD、Momentum、AdaGrad、Adam的基础上，增加RMSprop、Nesterov算法，全面总结它们的优缺点

先上两张很经典的图：

算法	优点	缺点	适用情况
批量梯度下降	目标函数为凸函数时，可以找到全局最优值	收敛速度慢，需要用到全部数据，内存消耗大	不适用于大数据集，不能在线更新模型
随机梯度下降	避免冗余数据的干扰，收敛速度加快，能够在线学习	更新值的方差较大，收敛过程会产生波动，可能落入极小值，选择合适的学习率比较困难	适用于需要在线更新的模型，适用于大规模训练样本情况
小批量梯度下降	降低更新值的方差，收敛较为稳定	选择合适的学习率比较困难
Momentum	能够在相关方向加速SGD，抑制振荡，从而加快收敛	需要人工设定学习率	适用于有可靠的初始化参数
Nesterov	梯度在大的跳跃后，进行计算对当前梯度进行校正	需要人工设定学习率
Adagrad	不需要对每个学习率手工地调节	仍依赖于人工设置一个全局学习率，学习率设置过大，对梯度的调节太大。中后期，梯度接近于0，使得训练提前结束	需要快速收敛，训练复杂网络时；适合处理稀疏梯度
Adadelta	不需要预设一个默认学习率，训练初中期，加速效果不错，很快，可以避免参数更新时两边单位不统一的问题。	训练后期，反复在局部最小值附近抖动	需要快速收敛，训练复杂网络时
RMSprop	解决 Adagrad 激进的学习率缩减问题	依然依赖于全局学习率	需要快速收敛，训练复杂网络时；适合处理非平稳目标 - 对于RNN效果很好
Adam	对内存需求较小，为不同的参数计算不同的自适应学习率	可能不收敛；可能错过全局最优解	需要快速收敛，训练复杂网络时；善于处理稀疏梯度和处理非平稳目标的优点，也适用于大多非凸优化 - 适用于大数据集和高维空间

总结

上学期最优化方法课程打了一点优化基础，但是都是很久远的优化算法，像牛顿法、拟牛顿法，现在很少用，因为这两个算法并不适用于高维数据。这次作业的主要目的就是学习目前的主流优化算法，打开网络结构优化调参的黑盒，做到知其然、知其所以然。参考了很多优秀博主的总结，理解了之后发现并不是很难，用到的数学原理也没有那么高深，还没有上学期最优化方法的数学原理复杂。

参考链接

NNDL 作业11：优化算法比较_HBU_David的博客-CSDN博客 

一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎

Adam那么棒，为什么还对SGD念念不忘 (2)—— Adam的两宗罪 - 知乎

Adam那么棒，为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略 - 知乎（2、3、4这三篇必看！！！）

 CS231n Convolutional Neural Networks for Visual Recognition

通俗解读SGD、Momentum、Nestero Momentum、AdaGrad、RMSProp、Adam优化算法_ZEERO~的博客-CSDN博客

SGD ,Adam,momentum等优化算法比较_吃水果不削皮的博客-CSDN博客_adam和sgd的优缺点 

https://arxiv.org/abs/1705.08292

http://Improving Generalization Performance by Switching from Adam to SGD