GMW协议
GMW协议由Goldreich等人提出,基于混淆电路(Garbled Circuit),支持多方的半诚实的安全计算协议。和之前所述的姚氏混淆电路估值方案的不同之处在于,GMW混淆电路估值方案不需要使用混淆真值表,因此没用混淆真值表带来的查表和加解密操作,节省了非常大的计算量和通信量。
混淆电路在上次的科普已经介绍过了,在将安全多方计算的目标函数转换为布尔电路后,通过对电路进行混淆(加密)操作来得到混淆电路。
混淆电路通过对电路进行混淆(加密)操作来掩盖电路的输入和电路的结构,以此来实现对各个参与者的隐私信息的保密,再通过电路计算来实现安全多方计算的目标函数的计算。
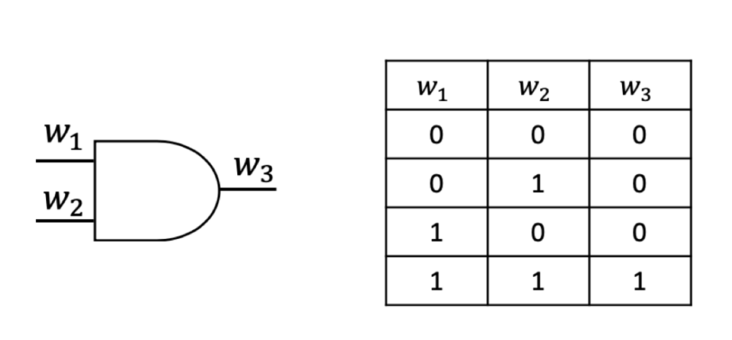
GMW协议的目标函数由异或门和与门、非门组成。非门的输出值是输入值的反,输入为1则输出为0,反之输入为0则输出为1。与门的真值表如下图所示: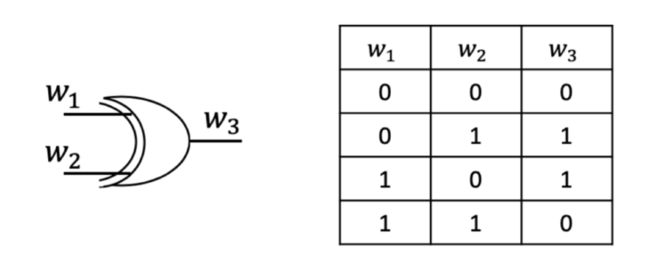
异或门及其真值表
首先介绍GMW协议的两方情况。首先假设参与者为Alice 和Bob,Alice和Bob的输入均为长为n的比特串,其中 Alice输入为比特串,Bob的输入为比特串b。
对于比特串中的每个比特\( _ \),Alice都产生一个随机的比特\( _{1} \)∈ {0,1},1≤≤,并将这n个随机产生的比特\( _{1} \),1≤≤发送给Bob。
对于比特串中的每个比特\( _ \),Bob也都产生一个随机的比特\( _{2} \)∈ {0,1},1≤≤,并将这n个随机产生的比特发送给Alice。Alice和Bob分别将\( a_{i} \oplus r_{1 i} \)和\( b_{i} \oplus r_{2 i} \)、\( _{1} \)、\( _{2} \)作为协议输入和b的子秘密。
即Alice掌握了和b的子秘密\( _{Alice} \)和\( _{Alice} \),\( _{Alice}= \oplus _{1} \),\( _{Alice}=_{2} \),Bob掌握了和b的子秘密\( a_{Bob}和_{Bob} \),\( a_{Bob}=_{1},_{Bob}= \oplus _{2} \)。
若Alice公开其所掌握的\( \oplus _{1}和_{2} \),Bob公开其所掌握的\( _{1}和\oplus _{2} \),那么Alice和Bob可以共同计算出\( =\oplus _{1}\oplus _{1},=\oplus_{2}\oplus_{2} \)。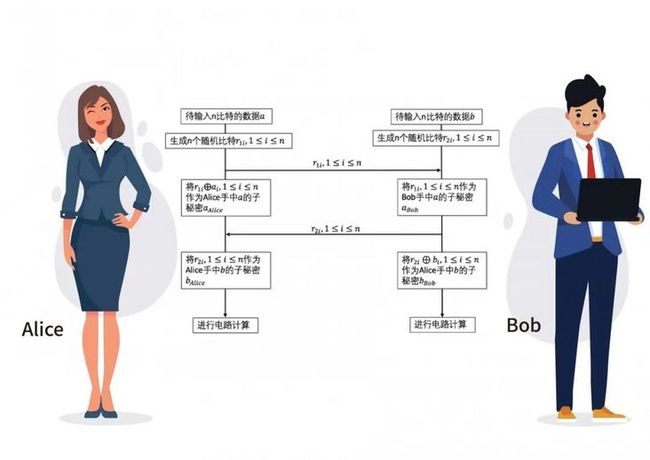
接着Alice和Bob对布尔电路中的每个门求值,直至完成整个电路的计算。对于非门,由于非门是单输入的,Alice和Bob间无须进行交互,因此直接对输入求反即可。
对于异或门,假设异或门的输入分别为和b,Alice掌握了和b的子秘密\( _{Alice}和_{Alice} \),Bob掌握了和b的子秘密\( a_{Bob}和_{Bob} \),因为:![]()
因此Alice和Bob可以在本地对其所掌握的子秘密进行计算, 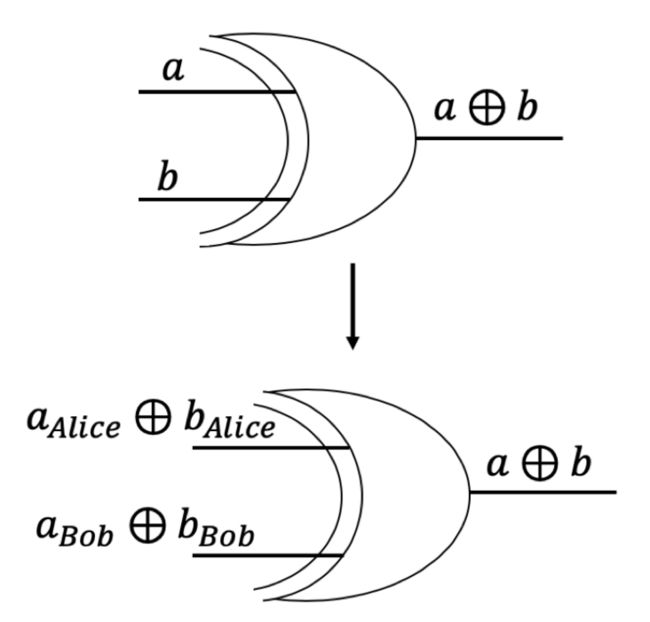
对于与门,因为\( ⋀=(_{Alice}\oplus a_{Bob})⋀(_{Alice}\oplus_{Bob}) \),因此Alice和Bob无法只在本地完成与门的计算。 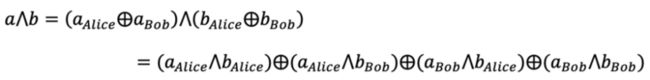
因为Alice手中有\( _{Alice}、_{Alice} \),因此Alice可以本地计算\( _{Alice}⋀{Alice} \)。Bob 手中有\( a{Bob}、{Bob} \),因此Bob可以本地计算\( a_{Bob}⋀_{Bob} \)。剩下的\( _{Alice}⋀_{Bob}和a_{Bob}⋀_{Alice} \)二者必须协同完成。
\( (_{Alice}⋀_{Bob})\oplus(a_{Bob}⋀_{Alice}) \)的计算可通过四选一不经意传输协议完成。对于Alice来说,Bob掌握的\( a_{Bob}和_{Bob} \)都是单比特值,只有四种情况: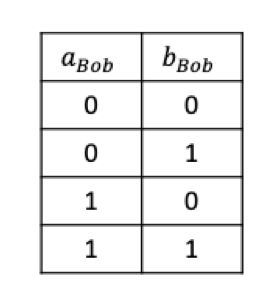
Alice手中又有\( _{Alice}和_{Alice} \),因此Alice可以直接计算出四种情况下的⋀的值,假设分别为\( _{00},_{01},_{01},_{11} \),注意这里⋀的值为\( (_{Alice}\oplus a_{Bob})⋀(_{Alice}\oplus _{Bob}) \)的值, 对于Alice和Bob来说式子里都只有两个未知数,而这两个未知数一共只有4种可能。
Alice的未知数为\( a_{Bob}和_{Bob} \),Alice可以假设(\( a_{Bob},_{Bob} \))分别为(0,0)、(0,1)、(1,0)、(1,1),那么根据假设的四种情况,\( _{Alice},_{Alice},a_{Bob},_{Bob} \)就都确定了,可以据此计算出四个确定的\( _{00},_{01},_{01},_{11} \)值。因此Alice可以得到下表: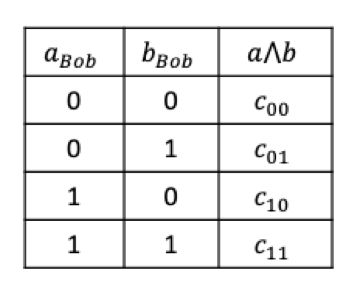
Alice 再产生一个随机比特,并将计算出的\( _{00},_{01},_{01},_{11} \)异或上随机比特,将\( _{00}\oplus, _{01}\oplus, _{01}\oplus, _{11}\oplus \)为四选一不经意传输协议的输入,Bob将其所掌握的\( a_{Bob}_{Bob} \)作为四选一不经意传输协议的输入,双方执行该OT协议,Bob得到对应的\( _{aBobBob}\oplus \)。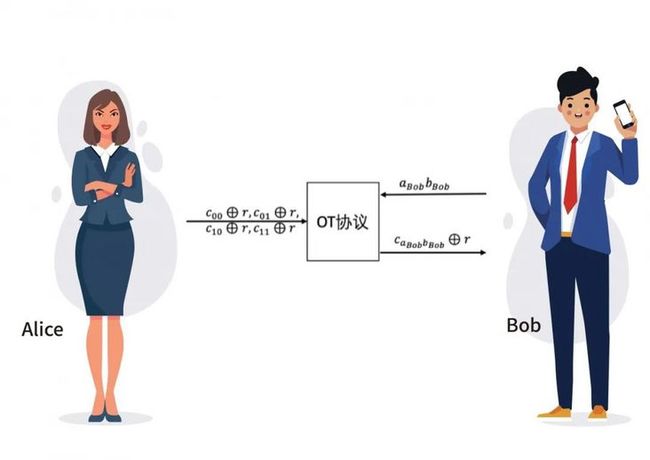
Alice将作为该与门的输出的子秘密,Bob将\( _{aBobBob}\oplus \)作为该与门的输出的子秘密。
由于Alice和Bob双方间执行的是不经意传输协议,Alice不知道Bob 在\( _{00}\oplus, _{01}\oplus, _{01}\oplus, _{11}\oplus \)中选择了哪个,保证了\( a_{Bob}_{Bob} \)依旧对Alice保密。
又由于Alice发送的是\( \oplus _{aBobBob} \),Bob不知道随机比特的值,也就不知道\( _{aBobBob} \)的到底是1还是0,只有在最后双方都公布各自手中的计算结果,双方才能合力计算出正确的结果。 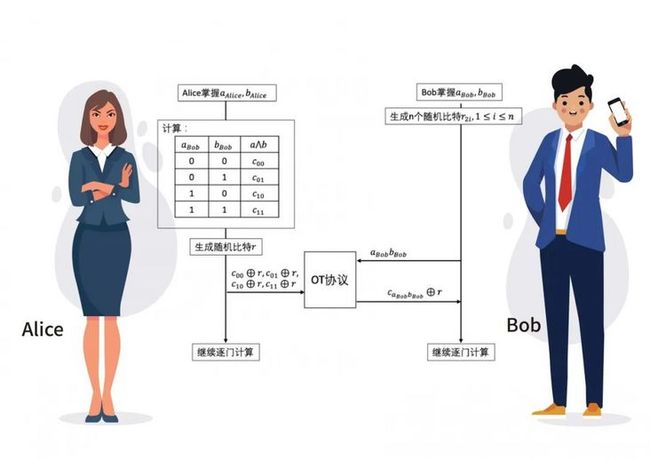
这里Bob得到的子秘密异或上Alice得到的子秘密即为⋀的值。
将GMW协议扩展到多方情况下:参与者为\( _1,_2,…,_ \),假设输入为m个比特,那么每个参与者\( _ \)产生组,每组−1个随机比特,分别将每组的−1个随机比特发送给除了自己之外的n-1个参加者。
假设输入数据为1个比特,那么每个参与者\( _ \)向参与者\( _ \)发送\( _{} \),1≤≤且≠。在所有参与者发送完成后,参与者\( _ \)掌握了\( _{1},_{2},…,_{} \)。假设\( _ \)的输入为,那么\( _ \)将\( \oplus _{1}\oplus _{2}\oplus…\oplus _{} \)作为的子秘密\( _ \)。
对应的收到\( _ \)发送的随机比特\( _{} \)的参与者\( _ \),将\( _{} \)当做秘密的子秘密\( _ \)。因此\( =_1\oplus_2\oplus…\oplus_ \)。
对于异或门以及非门,和双方情况下相同,每个参与者直接在本地进行计算即可。对于与门,与门的输入为和b,参与者\( _ \)手中掌握了和b的子秘密\( _和_ \),因为\( =_1\oplus_2\oplus…\oplus_,=_1\oplus_2\oplus…\oplus_ \),可得:![]()
这其中,对于\( _ \)来说,每个\( _⋀_ \)都可由\( _ \)在本地进行计算。而对于\( _⋀_ \),≠,可由参与者\( _和_ \)通过上述的两方BGW协议共同计算出\( _⋀_ \)的两个子秘密。当电路计算完成,每个参与者公布自己所掌握的子秘密,再将所有的子秘密进行异或,即可得到最后的计算结果。
BGW协议
BGW协议也是支持多方的安全计算协议,BGW协议基于Shamir(t, n)门限秘密共享机制,利用了Shamir秘密共享机制的加法同态和乘法同态的性质。Shamir(t, n)门限秘密共享机制在之前的科普已经进行过介绍了。
假设BGW协议的参与者一共有n人,假设参与者需要输入秘密,则参与者首先利用Shamir(t,n)门限秘密共享机制将秘密共享给其他所有参与者,阈值t的选择根据具体使用情景下的安全性要求决定。
当所有参与者的输入都通过Shamir(t, n)门限秘密共享机制分享后,每个参与者都掌握了协议输入的子秘密。假设一个门的输入分别为和,秘密和已经分别由秘密分配函数\( f_{a}(x)=\alpha_{\mathrm{t}-1} x^{\mathrm{t}-1}+\cdots+\alpha_{1} x^{1}+a, f_{b}(x)=\beta_{\mathrm{t}-1} x^{\mathrm{t}-1}+\cdots+\beta_{1} x^{1}+b \)分配完成,\( _(0)=,_(0)= \),参与者\( _ \)掌握和b的子秘密\( _,_ \)。在布尔电路上,可将异或门和与门分别看成在有限域2上的加法和乘法。将异或用模为2的加法进行计算,与用模为2的乘法进行计算。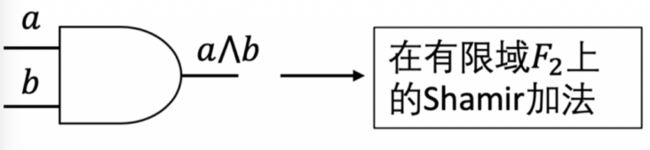
对于异或门:由于Shamir具有加法同态性,因此
\( a \oplus b=f_{a}(0) \oplus f_{b}(0), f_{a}(x) \oplus f_{b}(x)=\left(\alpha_{\mathrm{t}-1}+\beta_{\mathrm{t}-1}\right) x^{\mathrm{t}-1}+\cdots+\left(\alpha_{1}+\beta_{1}\right) x^{1}+(a+b) \)
假设\( _()=_()\oplus _() \),则\( _()=_()\oplus_() \),而\( _()=_和_()=_都由_掌握 \),因此\( _ \)可以本地计算出\( _()=_+_ \)。当所有计算完成后,每个参与者\( _ \)公布自己计算出的\( _() \), 即可恢复出\( _()和_(0) \)。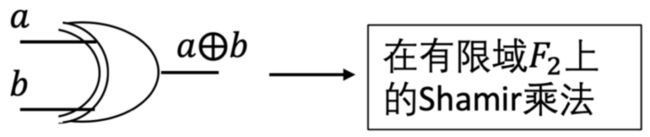
对于与门,和之前叙述过的基于Shamir(t, n)门限共享机制的多方乘法计算相同,只是BGW是在有限域2上。每个参与者\( _计算_=__ \),\( 接着每个_独自选取次数为t次的随机多项式ℎ_(),且满足ℎ_(0)=_,1≤≤,
向各个参与者分配\( _ \),且\( _{}= ℎ_() \),1≤,≤。所有参与者分配结束后,掌握了信息\( _{1},_{2},…,_{} \),同时再利用公开的重组向量\( \lambda _1,…,\lambda _ \),\( _ \)计算\( c_{i}=\sum_{j=1}^{n} \lambda_{j} c_{j i} \)。
此时\( _ \)掌握的子秘密\( _ \)即为的子秘密。当所有计算完成后,每个参与者公开自己的子秘密,再根据之前叙述的Shamir(t, n)门限秘密重构算法即可获得。