Entropy-based Active Learning for Object Detection with Progressive Diversity Constraint（CVPR2022）

原文链接

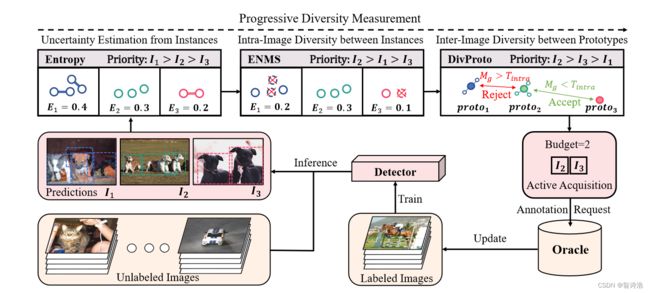
根据overview来阐述过程

主要分为三步：

1. Instance uncertainty is first computed based on the entropy.
2. ENMS then performs on each image to remove redundant instances.
3. DivProto aggregates the instances of each image to prototypes and rejects the images close to the selected ones.

Problem Statement

args

Candidate images: $\{I_i{\}}_{i\in [n]}$
Selected images: $\mathcal{S}=\{I_{s(j)}|s(j)\in [n]{\}}_{j\in [m]}$¹
Budget: $b$
Detect model: $D_{\mathcal{S}}$

each cycle:

Acquire a image subset: $\Delta \mathcal{S}$ from $\mathcal{S}$ ensure $|\Delta \mathcal{S}|=b$.
Then: update $\mathcal{S}:=\mathcal{S}\cup \Delta \mathcal{S}$
Then: oracle provide labels:$\mathcal{Y}=\{y_{s(j)}{\}}_{j\in [m]}$
Then: train $D_{\mathcal{S}}$ by $\mathcal{S}$ and $\mathcal{Y}$

Target and meathods

Target

AL 被定义为最小化一个Core-set loss: ${\sum }_{i\in [n]}l(I_i,y_i;D_{\mathcal{S}})$²

作者将detestor $D_{\mathcal{S}}$拆分为两个步骤：
$D_{\mathcal{S}}=P_{\mathcal{S}}+A_{\mathcal{S}}$
$P_{\mathcal{S}}$是encoder
$A_{\mathcal{S}}$是predictor
encoder：$\{po{s}_k{\}}_{k\in [t]}\Rightarrow feature$³

$A_{\mathcal{S}}(P_{\mathcal{S}}(I_i))=\{{\tilde{y}}_{i,k},c_{i,k},p_{i,k}{\}}_{k\in [t]}$⁴

那么core-set loss可以拆分为每个实例loss的和，但是作者认为这样不好，因为Lipschitz continuous的问题

Step.1

作者采用instance-level的熵公式：
$\mathbb{H}\left(I_i,k\right)=-p_{i,k}\log p_{i,k}-\left(1-p_{i,k}\right)\log \left(1-p_{i,k}\right)$
那么image-level就是instance熵的和，作者基于这个和对图片进行排序，选择top-$K$个作为acquisition set$\Delta \mathcal{S}$

也就是第一步：Instance uncertainty is first computed based on the entropy

Step.2 ENMS

然后作者说As visually similar bounding boxes contain redundant information which are not preferred when training robust detectors
所以要select the most informative ones and abandon the rest
作者说这种冗余不仅存在于instance-level也存在于image-level中，但是目前没有什么方法能去除，所以作者提出了一个hybrid approach达到了considers the instance-level evaluation and achieves the image-level acquisition in the mean time的效果。

重新阐述一下overview中的三个步骤就是：

1. uncertainty estimation using the basic detection entropy
2. Entropy-based Non-Maximum Suppression (ENMS)
3. the diverse prototype (DivProto) strategy.

上面介绍的熵排序就是第一步从数量上measure the image-level uncertainty from object instances.

随后提出了基于熵的ENMS去除冗余信息的方法，从而加强了图像中的实例级多样性。

最后DivProto通过将实例级的多样性转换为类间和类内的多样性，进一步确保了跨图像的实例级多样性。

层次结构：
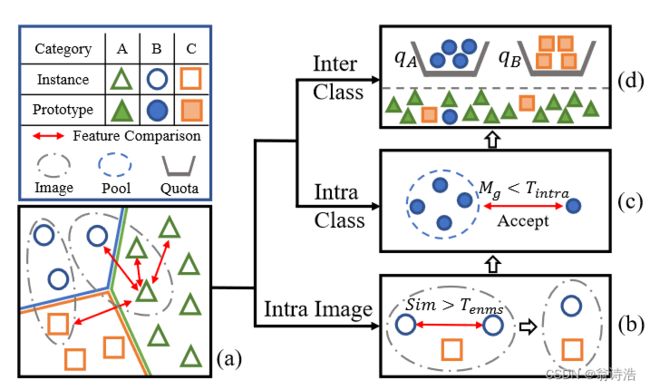The overall instance-level diversity (a) is divided into the intra-image diversity (b) via ENMS and the inter-image diversity is accomplished by DivProto, which is then decomposed into the inter-class and intra-class ones as shown in © and (d), respectively.

下面介绍ENMS
作者说object detectors often generate a large amount of proposal bounding boxes with heavy overlaps，那么目前的解决方案就是NMS在此基础上，将属于同一实例的边界框合并为统一的边界框。但是NMS无法处理instance-level的冗余，这里要注意的是NMS处理的是一个实例的冗余，而ENMS处理的是实例之间的冗余。

这里的E就是Entropy-based

ENMS作为NMS的successive step

ENMS首先计算两两instance的余弦距离:
$\mathrm{Sim}\left({\mathbf{f}}_{i,k},{\mathbf{f}}_{i,j}\right)=\frac{{\mathbf{f}}_{i,k}^T\cdot {\mathbf{f}}_{i,j}}{\Vert {\mathbf{f}}_{i,k}\Vert \Vert {\mathbf{f}}_{i,j}\Vert }$
${\mathbf{f}}_{i,j}$就是image $I_i$ 的instance $k$通过encoder $P_{\mathcal{S}}$得到的特征。

然后ENMS就工作在index集合$S_{ins}$上：

ENMS得到的是一个值$E_i$它是属于image-level的一个熵，它相当于是优化了Step1中作者定义的$\mathbb{H}$

Step.3 DivProto

ENMS增强了图像内和图像间的多样性，也就是说，图像之间的冗余仍然存在

作者定义了一个prototype量：
$\mathbf{prot}{\mathbf{o}}_{\mathbf{i},\mathbf{c}}=\frac{{\sum }_{k\in [t]}1(c,c_{i,k})\cdot \mathbb{H}(I_i,k)\cdot {\mathbf{f}}_{\mathbf{i},\mathbf{k}}}{{\sum }_{k\in [t]}1(c,c_{i,k})\cdot \mathbb{H}(I_i,k)}$⁵

下面介绍DivProto
分为两步
首先是Intra-class Diversity
首先按照$E_i$进行排序(降序)，给定一个candidata image $I_i$和acquired set $\Delta \mathcal{S}$的prototype值，那么$I_i$的intra-class diversity量可以定义为：
$M_g(I_i,[C])=\underset{c\in [C]}{\min }\underset{j\in |\Delta \mathcal{S}|}{\max }Sim(\mathbf{prot}{\mathbf{o}}_{\mathbf{j},\mathbf{c}},\mathbf{prot}{\mathbf{o}}_{\mathbf{i},\mathbf{c}})$

意思就是对于$I_i$的所有instance的每个类求一个值，这个值是max的prototype余弦角度的最大值，也就是在$\Delta \mathcal{S}$中找一个与此类最大的相似度，然后取所有类相似度的下限值(min)表示整张图片与$\Delta \mathcal{S}$的相似度

当$M_g(I_i,[C])$大于一个阈值的时候就可以把它reject掉，因为这与$\Delta \mathcal{S}$相似很大了，放进去没价值

然后是inter-class Diversity
上一步有一个缺陷，就是favor certain classes，即可能会导致偏向于一个类，导致类别不平均，这一步就是解决这个问题。

作者的解决思路是adaptively providing more budgets for the minority classes than the majority ones.这里不做详细介绍

$TheEnd.$

---

1. $i,j$为index,$n,m$为Candidate set和Selected set的图片数量,$[n]=\{1,\cdots ,n\}$and $[m]=\{1,\cdots ,m\}$ ↩︎

2. $y_i$ 是$I_i$的潜在label。 ↩︎

3. $k$即一个图片中的实例index, $t$就是实例个数 ↩︎

4. ${\tilde{y}}_{i,k},c_{i,k},p_{i,k}$分表表示boundingbox,class,confidence ↩︎

5. $1(c,c_{i,k})$=1 iff $c=c_{i,k}$ ↩︎