机器学习opencv对分类-回归算法的应用
机器学习对分类与回归评分指标不同
在sklearn中评分函数score相当于calcError(评价模型的类函数),fit(拟合函数)相当于train(训练函数)
常见的评分指标都在sklearn.metrics里
这里写目录标题
- 分类指标
-
- 准确率
- 精确率
- 召回率
- 回归指标
-
- 均方误差(mse)
- 可释误差
- R 2 R^{2} R2
- 分类模型
-
- 输出结果
- 回归模型
-
- 输出结果
分类指标
准确率
from sklearn import metrics
metrics.accuracy_score(y_true, y_pred)
精确率
from sklearn import metrics
metrics.precision_score(y_true, y_pred)
召回率
from sklearn import metrics
metrics.recall_score(y_true, y_pred)
回归指标
均方误差(mse)
from sklearn import metrics
metrics.mean_squared_error(y_true, y_pred)
#mse = np.mean((y_true-y_pred)**2)
可释误差
from sklearn import metrics
metrics.explained_variance_score(y_true, y_pred)
#fvu = np.var(y_true-y_pred)/np.var(y_ture)
#var代表方差,fvu代表可释误差
R 2 R^{2} R2
from sklearn import metrics
metrics.r2_score(y_true, y_pred)
#r2 = 1.0-mse/np.var(y_ture)
R 2 R^{2} R2越接近1,预测值越接近实际值
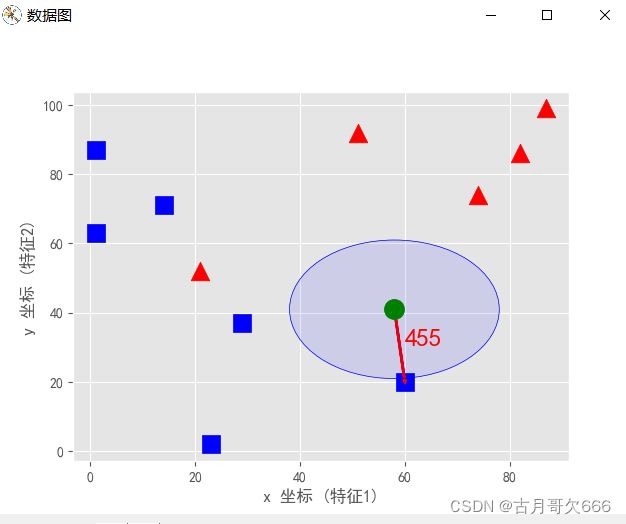
分类模型
利用opencv分类模型预测类别,以KNN算法为例
from turtle import color
import cv2
from matplotlib import markers
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
############参数设置################
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.style.use("ggplot")
np.random.seed(42)
############定义训练数据集###########
"""
num_samples:代表数据样本个数,表示行
num_features=2:代表数据特征个数,表示列
返回一个行列表示的数组,每个数据样本的标签
"""
def generate_data(num_samples, num_features=2):
data_size = (num_samples, num_features)
data = np.random.randint(0, 100, size=data_size)
label_size = (num_samples, 1)
labels = np.random.randint(0, 2, size=label_size)
#opencv对数据类型要求将数据点类型转换为np.float32
return data.astype(np.float32), labels
#输入shape:11*2
#训练集
train_data, labels = generate_data(11)
#测试集
newcomer, _ = generate_data(1)
###############绘制数据############
#定义绘图函数
def plot_data(all_biue, all_red):
fig =plt.figure("数据图")
ax = fig.add_subplot(111) # 111代表1*1的图的第一个子图
plt.scatter(all_biue[:, 0], all_biue[:, 1], c="b", marker="s", s=180)
plt.scatter(all_red[:, 0], all_red[:, 1], c="r", marker="^", s=180)
plt.plot(newcomer[0, 0], newcomer[0, 1], "go", markersize=14)
plt.arrow(newcomer[0, 0], newcomer[0, 1], 60-newcomer[0, 0], 20-newcomer[0, 1],
head_width=0.2, color="red", lw=2,length_includes_head = True) # 坐标与距离
#直接plt.Circle()不显示图片,需要用轴区域,或者当前图的子图画
circle = Circle(xy=(newcomer[0, 0], newcomer[0, 1]), radius=20, alpha=0.1, color='b')
ax.add_patch(circle)
circle = plt.Circle((newcomer[0, 0], newcomer[0, 1]), 20, color='b', fill=False)
plt.gcf().gca().add_artist(circle)
plt.text(60, 30, s="455", fontsize = 18, color = 'red')
plt.xlabel("x 坐标 (特征1)")
plt.ylabel("y 坐标 (特征2)")
plt.show()
#ravel(),平面化数组
blue = train_data[labels.ravel()==0]
red = train_data[labels.ravel()==1]
plot_data(blue, red)
##########训练分类器###############
knn = cv2.ml.KNearest_create()
knn.train(train_data,cv2.ml.ROW_SAMPLE,labels)
###########预测新数据##############
ret, results, neighbor, dist = knn.findNearest(newcomer, 1)
print("Predicted label:\t", results)
print("Neighbor's label:\t", neighbor)
print("Distance to neighbor:\t", dist)
输出结果
回归模型
利用opencv回归模型预测值,以线性回归算法为例
import numpy as np
from sklearn import datasets
from sklearn import metrics
from sklearn import model_selection as modsel
from sklearn import linear_model
import matplotlib.pyplot as plt
##########设置参数###############
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.style.use("ggplot")
############载入数据集###########
"""
booton.data:(506,13)
booton.target:(506,)
"""
booton = datasets.load_boston()
#拆分数据集
x_train, x_test, y_train, y_test = modsel.train_test_split(
booton.data, booton.target, test_size=0.1, random_state=42)
##############训练模型###########
linreg = linear_model.LinearRegression()
linreg.fit(x_train, y_train)
#均方误差
train_mse = metrics.mean_squared_error(y_train, linreg.predict(x_train))
#R方值
train_r2 = linreg.score(x_train, y_train)
##############测试模型############
y_pred = linreg.predict(x_test)
test_mse = metrics.mean_squared_error(y_test, y_pred)
test_r2 = linreg.score(x_test, y_test)
##########误差可视化##############
#测试值与预测值可视化
plt.figure("误差可视化", figsize=(13,6))
ax = plt.subplot(121)
ax.set_title("测试值与预测值可视化")
plt.plot(y_test, linewidth=3, label="真实值")
plt.plot(y_pred, linewidth=3, label="预测值")
plt.legend(loc="best")
plt.xlabel("测试数据点")
plt.ylabel("目标值")
#R方值可视化
ax = plt.subplot(122)
ax.set_title("R方值可视化")
plt.plot(y_test, y_pred, "o")
plt.plot([-10,60], [-10,60], "k--")
plt.axis([-10,60,-10,60])
plt.xlabel("真实值")
plt.ylabel("预测值")
scorestr = r"R$^2$ = %.3f" % test_r2
errstr = "MSE = %.3f" % test_mse
plt.text(-5, 50, scorestr, fontsize=12)
plt.text(-5, 45, errstr, fontsize=12)
plt.show()
输出结果

从上图可以看出二图通过描述离散数据情况,与对角线存在偏差表明模型的预测出现了一些误差或者是数据中有一些方差是模型无法解释的, R 2 R^{2} R2表明我们可以解释数据76%的离散程度,其中均方误差为14.996.