R语言单因素分析案例
1单因素方差分析实例1:在R中, aov() 函数提供了方差分析表的计算:
进行方差分析的步骤:
a.用数据框的格式输入数据:如:lamp<-data.frame(X=c() , A=factor() )
b.调用aov() 函数计算方差分析:lamp.aov<-aov(X~A, data=lamp
c.用summary() 提取方差分析的信息
summary(lamp.aov) (anova.tab(lamp.aov) )
1单因素方差分析实例1
X<-c(1600,1610,1650,1680,1700,1720,1800,1580,1640,1640,1700,1750,1460,1550,1600,1620,1640,1740,1660,1820,1510,1520,1530,1570,1680,1600)
A<-factor(c(rep(1,7) , rep(2,5), rep(3,8), rep(4, 6) ) ) # 重复次数函数rep
lamp<-data.frame(X,A)
lamp.aov<-aov(X~A,data=lamp)
summary(lamp.aov)
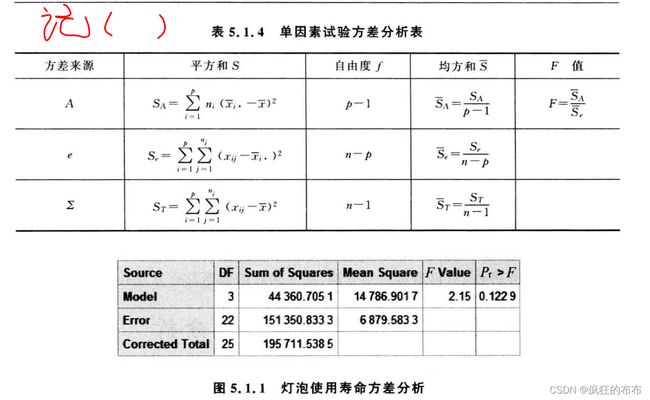
Df Sum Sq Mean Sq F value Pr(>F)
A 3 44361 14787 2.149 0.123
Residuals 22 151351 6880
>
1单因素方差分析实例1
分析上述计算结果, Df表示自由度, Sum Sq表示平方和, Mean Sq表示
均方, F value是F值, Pr(>F) 是p值, A即为因子A, Residuals是残差。
从P值(0.121>0.05)可以看出,没有充分理由拒绝零假设H0,也就是说,
4种材料生产出来的零件寿命没有显著差异
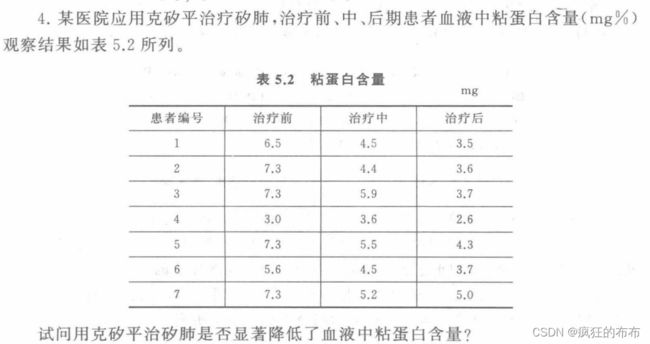
课后习题4
> X4<-c(6.5,7.3,7.3,3.0,7.3,5.6,7.3,4.5,4.4,5.9,3.6,5.5,4.5,5.2,3.5,3.6,3.7,2.6,4.3,3.7,5.0)
> A4<-factor(c(rep(1,7),rep(2,7),rep(3,7)))
> A4
[1] 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 3
Levels: 1 2 3
> lamp4<-data.frame(X4,A4)
> lamp4.aov<-aov(X4~A4,data=lamp4)
> summary(lamp4.aov)
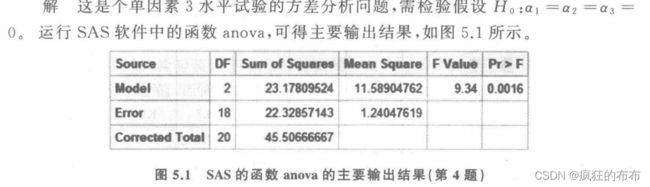
Df Sum Sq Mean Sq F value Pr(>F)
A4 2 23.18 11.59 9.342 0.00165 **
Residuals 18 22.33 1.24
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
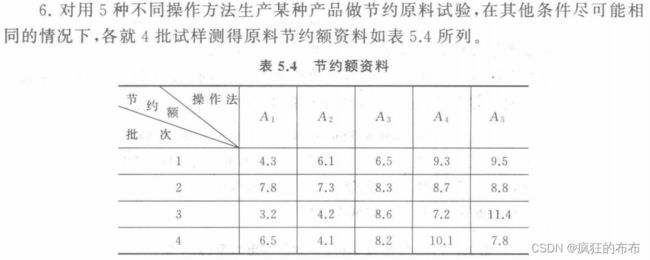
课后习题6
> X6<-c(4.3,7.8,3.2,6.5,6.1,7.3,4.2,4.1,6.5,8.3,8.6,8.2,9.3,8.7,7.2,10.1,9.5,8.8,11.4,7.8)
> A6<-factor(c(rep(1,4),rep(2,4),rep(3,4),rep(4,4),rep(5,4)))
> A6
[1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5
Levels: 1 2 3 4 5
> lamp6<-data.frame(X6,A6)
> lamp6
X6 A6
1 4.3 1
2 7.8 1
3 3.2 1
4 6.5 1
5 6.1 2
6 7.3 2
7 4.2 2
8 4.1 2
9 6.5 3
10 8.3 3
11 8.6 3
12 8.2 3
13 9.3 4
14 8.7 4
15 7.2 4
16 10.1 4
17 9.5 5
18 8.8 5
19 11.4 5
20 7.8 5
>
> lamp6.aov<-aov(X6~A6,data=lamp6)
> summary(lamp6.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A6 4 55.54 13.884 6.059 0.00416 **
Residuals 15 34.37 2.292
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>