脑电EEG代码开源分享 【4.特征提取-时域篇】

往期文章

希望了解更多的道友点这里
0. 分享【脑机接口 + 人工智能】的学习之路
1.1 . 脑电EEG代码开源分享 【1.前置准备-静息态篇】
1.2 . 脑电EEG代码开源分享 【1.前置准备-任务态篇】
2.1 . 脑电EEG代码开源分享 【2.预处理-静息态篇】
2.2 . 脑电EEG代码开源分享 【2.预处理-任务态篇】
3.1 . 脑电EEG代码开源分享 【3.可视化分析-静息态篇】
3.2 . 脑电EEG代码开源分享 【3.可视化分析-任务态篇】
4.1 . 脑电EEG代码开源分享 【4.特征提取-时域篇】
4.2 . 脑电EEG代码开源分享 【4.特征提取-频域篇】
4.3 . 脑电EEG代码开源分享 【4.特征提取-时频域篇】
4.4 . 脑电EEG代码开源分享 【4.特征提取-空域篇】
5 . 脑电EEG代码开源分享 【5.特征选择】
6.1 . 脑电EEG代码开源分享 【6.分类模型-机器学习篇】
6.2 . 脑电EEG代码开源分享 【6.分类模型-深度学习篇】
汇总. 专栏：脑电EEG代码开源分享【文档+代码+经验】

0 . 【深度学习】常用网络总结

---

---

一、前言

本文档旨在归纳BCI-EEG-matlab的数据处理代码，作为EEG数据处理的总结，方便快速搭建处理框架的Baseline，实现自动化、模块插拔化、快速化。本文以任务态（锁时刺激，如快速序列视觉呈现）为例，分享脑电EEG的分析处理方法。
脑电数据分析系列。分为以下6个模块：

1. 前置准备
2. 数据预处理
3. 数据可视化
4. 特征提取（特征候选集）
5. 特征选择（量化特征择优）
6. 分类模型

本文内容：【4. 特征提取-频域篇】

提示：以下为各功能代码详细介绍，若节约阅读时间，请下滑至文末的整合代码

---

二、特征提取 框架介绍

特征提取作为承上启下的重要阶段，是本系列中篇幅最长的部分。承上，紧接预处理结果和可视化分析，对庞大的原始数据进行凝练，用少量维度指标表征整体数据特点；启下，这些代表性、凝练性的特征指标量化了数据性能，为后续的认知解码、状态监测、神经调控等现实需求提供参考。

特征提取的常用特征域为时域、频域、时频域、空域等。本文特征主要为手动设置的经验特征，大多源于脑科学及认知科学的机制结论，提取的特征具有可解释的解剖、认知、物理含义；也有部分是工程人员的实践发现，在模型性能提升中效果显著。

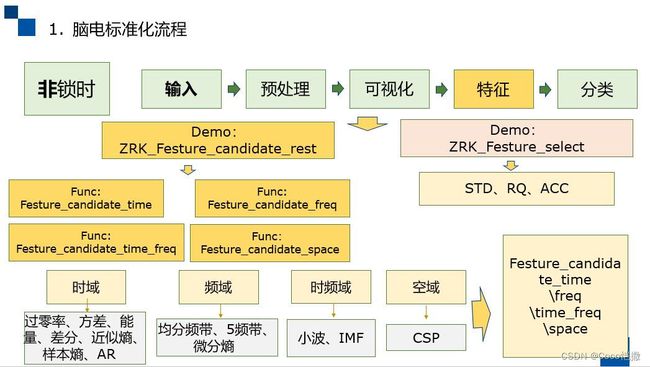
特征提取的代码框图、流程如下所示：

时域-特征提取的主要功能，分为以下2部分：

• 统计特征：过零率、标准差、能量、差分、AR等
• 熵类特征：近似熵、样本熵、李雅普诺夫指数、混合熵等

统计特征是脑电数据最初的刻画方式，前人认为脑电信号属于信号分析的一种，便引入常用的统计学指标来刻画。统计学指标大家比较熟悉，需要对一定时间窗内的数据统计分析，因此对于长时间的脑电信号更友好。统计学指标大多具有现实含义，如过零率代表信号沿零值翻转频率，标准差表示数据偏离均值程度，差分特征表示离散点间的变化速率等。
近期文献中越来越多使用高阶数特征，例如高阶中心距、高阶远点距等，文献中解释说高阶特征包含丰富脑电信息。本人也应用过高阶特征在分类任务中，确实会提升分类性能，但是存在比较严重的过拟合问题，由于高阶特征的高幂特性导致数值指数级增长 or 降低，无论是否后续归一化都会影响特征分布，建议在开集测试分类中慎用。并且其对应的认知含义还不清，仍期待更多的研究进展。

时域-统计学特征：

时域-熵类特征：
熵类特征在近期成为脑电处理的热门话题，文献中声明的熵类特征均有不错性能，例如近似熵、样本熵、李雅普诺夫指数、混合熵等，本人在研究中也发现部分熵类确实提高准确率，推荐大家尝试。
熵类特征的主要思想在于其非线性，通过e或者log计算获得非线性表现。个人根据e或者log曲线认为，熵类特征通过 拉伸 或 压缩 原特征数值，对原特征产生畸变效果，主要决定因素还是原特征的取值范围。熵类特征依靠经验较难，更推荐大家广撒网的尝试，还要注意是否特征进行归一化和标准化。熵类特征也存在短板，例如计算时间明显长于线形特征，并且熵类特征具体含义细节也需要进一步研究。

---

三、代码格式说明

本文非锁时任务态（下文以静息态代替）范例为：ADHD患者、正常人群在静息状态下的脑模式分类

• 代码名称：代码命名为Festure_ candidate_xxx (time / freq/ imf/ space)
• 参数设置：预处理结果\采样率\时域是否非线性熵特征（耗时）\频域均分分辨度\imf阶数\space对比通道数及频带范围。
• 输入格式：输入格式承接规范预处理最后一项输出，Proprocess_xxx(预处理最终步骤)_target/nontarget。
• 输出及保存格式：输出格式为试次数*特征个数，按照除空域特征外，按照通道的特征拼接，先为1通道内的所有特征，接着2通道的所有特征。保存文件名称为Festure_candidate_xxx(特征域名称)_target/nontarget。

---

三、脑电特征提取 代码

提示：代码环境为 matlab 2018

3.0 参数设置

可视化内容可以选择，把希望可视化特征域写在Featute_content 中

• 一次进行10人次的批处理，subject_num = [1;10]
• 特征提取内容： Featute_content = [‘time’,‘freq’,‘time_freq’,‘space’]; 时域、频域、时频域、空域均分析
• 时域特征内容：过零率，标准差、近似熵，样本熵，AR。Featute_time_content = [‘cross_zero’,‘std’,‘apen’,‘sampentropy’,‘ar’];

%% 0.特征候选集-参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data_path = 'C:\Users\EEG\Desktop\basetest_flod\save_fold\';
svae_path = 'C:\Users\EEG\Desktop\basetest_flod\save_fold\';

subject_num = [1;10];

% Featute_content = ['time\','freq\','time_freq\','space'];
Featute_content = ['time\','freq\','time_freq\'];
% Featute_time_content = ['cross_zero\','std\','apen\','sampentropy\','ar\'];
Featute_time_content = ['cross_zero\','std\','ar\'];
disp(['||特征候选集-参数设置||']);
disp(['特征域内容: ' , Featute_content]);
disp(['时域-候选集: ' , Featute_time_content]);

3.1 标准输入赋值

导入上一步预处理阶段处理后的数据：

%% 1.标准输入赋值
Proprocess_target_file = load([data_path ,'Proprocess_target_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))]);
Proprocess_nontarget_file = load([data_path ,'Proprocess_nontarget_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))]);
stuct_target_name =  'Proprocess_target';
stuct_nontarget_name =  'Proprocess_nontarget';

Proprocess_target_data = Proprocess_target_file.(stuct_target_name).data;
Proprocess_nontarget_data = Proprocess_nontarget_file.(stuct_nontarget_name).data;

subject_num = Proprocess_target_file.(stuct_target_name).subject_num;
fs_down = Proprocess_target_file.(stuct_target_name).fs_down;

remain_trial_target = Proprocess_target_file.(stuct_target_name).remain_trial;
remain_trial_nontarget = Proprocess_nontarget_file.(stuct_nontarget_name).remain_trial;

disp(['目标试次剩余: ' , num2str(remain_trial_target),'||平均： ', num2str(mean(remain_trial_target))]);
disp(['非目标试次剩余: ' , num2str(remain_trial_nontarget),'||平均： ', num2str(mean(remain_trial_nontarget))]);

3.2 时域-特征提取

主函数中 调用时域提取函数

主体调用函数Festure_candidate_time

%% 2.时域特征候选集
if contains(Featute_content,'time')
disp(['时域特征计算中...']);
tic;
[Festure_time_target,Festure_time_candidate_num_target]= Festure_candidate_time(Proprocess_target_data,Featute_time_content,remain_trial_target);    
[Festure_time_nontarget,Festure_time_candidate_num_nontarget]= Festure_candidate_time(Proprocess_nontarget_data,Featute_time_content,remain_trial_nontarget);    
t_time_candidate_cost = toc;

Festure_candidate_time_target = [];
Festure_candidate_time_target.data  = Festure_time_target;
Festure_candidate_time_target.Featute_time_content  = Featute_time_content;
Festure_candidate_time_target.remain_trial_target  = remain_trial_target;
Festure_candidate_time_target.Festure_time_candidate_num_target  = Festure_time_candidate_num_target;
Festure_candidate_time_target.fs_down = fs_down;

Festure_candidate_time_nontarget = [];
Festure_candidate_time_nontarget.data  = Festure_time_nontarget;
Festure_candidate_time_nontarget.Featute_time_content  = Featute_time_content;
Festure_candidate_time_nontarget.remain_trial_nontarget  = remain_trial_nontarget;
Festure_candidate_time_nontarget.Festure_time_candidate_num_nontarget  = Festure_time_candidate_num_nontarget;
Festure_candidate_time_nontarget.fs_down = fs_down;

disp(['时域特征计算完毕，耗时： ',num2str(t_time_candidate_cost)]);
disp(['时域特征保存中...']);
save([ svae_path , 'Festure_candidate_time_target_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))],'Festure_candidate_time_target');
save([ svae_path , 'Festure_candidate_time_nontarget_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))],'Festure_candidate_time_nontarget');
disp(['时域特征保存完毕']);
end

3.2.1 过零率 特征

function [Festure_time,Festure_time_candidate_num]= Festure_candidate_time(Standard_input_data,Featute_time_content,remain_trial)

%% 1.cross_zero
cross_zero = [];
if contains(Featute_time_content,'cross_zero')
cross_zero = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
cross_zero_channel_temp = zeros(1,size(Standard_input_data{1,1},1));
for channel_loop = 1:size(Standard_input_data{1,1},1)
    for point_loop = 1:size(Standard_input_data{1,1},2)-1
    if Standard_input_data{trial_loop,sub_loop}(channel_loop,point_loop) * Standard_input_data{trial_loop,sub_loop}(channel_loop,point_loop+1)<0
    cross_zero_channel_temp(1,channel_loop) = cross_zero_channel_temp(1,channel_loop) + 1;
    end
    end
end
cross_zero(count_trial,:) = cross_zero_channel_temp;   
count_trial = count_trial+1;
end
end
end

3.2.2 标准差 特征

%% 2.std
fest_std = [];
if contains(Featute_time_content,'std')
fest_std = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
std_temp  = [];
std_temp  = std(Standard_input_data{trial_loop,sub_loop}');
fest_std(count_trial,:) = std_temp;
count_trial = count_trial+1;    
end
end
end

3.2.3 近似熵 特征（计算时间较长）

%% 3.近似熵 
fest_apen = [];
if contains(Featute_time_content,'apen')
r_apen = 0.2*fest_std';    
fest_apen_2 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
fest_apen_3 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;

for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
for channel_loop = 1:size(Standard_input_data{1,1},1)
fest_apen_2(count_trial,channel_loop) = ApEn( 2, r_apen(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
fest_apen_3(count_trial,channel_loop) = ApEn( 3, r_apen(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
end
count_trial = count_trial+1;    
end
end

fest_apen = [fest_apen_2 fest_apen_3];
end

近似熵函数：

function apen = ApEn( dim, r, data, tau )
%ApEn
%   dim : embedded dimension
%   r : tolerance (typically 0.2 * std)
%   data : time-series data
%   tau : delay time for downsampling

%   Changes in version 1
%       Ver 0 had a minor error in the final step of calculating ApEn
%       because it took logarithm after summation of phi's.
%       In Ver 1, I restored the definition according to original paper's
%       definition, to be consistent with most of the work in the
%       literature. Note that this definition won't work for Sample
%       Entropy which doesn't count self-matching case, because the count
%       can be zero and logarithm can fail.
%
%       A new parameter tau is added in the input argument list, so the users
%       can apply ApEn on downsampled data by skipping by tau.
%---------------------------------------------------------------------
% coded by Kijoon Lee,  kjlee@ntu.edu.sg
% Ver 0 : Aug 4th, 2011
% Ver 1 : Mar 21st, 2012
%---------------------------------------------------------------------
if nargin < 4, tau = 1; end
if tau > 1, data = downsample(data, tau); end

N = length(data);
result = zeros(1,2);

for j = 1:2
    m = dim+j-1;
    phi = zeros(1,N-m+1);
    dataMat = zeros(m,N-m+1);

    % setting up data matrix
    for i = 1:m
        dataMat(i,:) = data(i:N-m+i);
    end

    % counting similar patterns using distance calculation
    for i = 1:N-m+1
        tempMat = abs(dataMat - repmat(dataMat(:,i),1,N-m+1));
        boolMat = any( (tempMat > r),1);
        phi(i) = sum(~boolMat)/(N-m+1);
    end

    % summing over the counts
    result(j) = sum(log(phi))/(N-m+1);
end

apen = result(1)-result(2);

end

3.2.4 样本熵 特征（计算时间较长）

%% 4.样本熵 
fest_sampentropy = [];
if contains(Featute_time_content,'sampentropy')
r_sampentropy = 0.2*fest_std';    
fest_sampentropy_2 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
fest_sampentropy_3 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;

for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
for channel_loop = 1:size(Standard_input_data{1,1},1)
fest_sampentropy_2(count_trial,channel_loop) = SampEntropy( 2, r_sampentropy(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
fest_sampentropy_3(count_trial,channel_loop) = SampEntropy( 3, r_sampentropy(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
end
count_trial = count_trial+1;    
end
end

fest_sampentropy = [fest_sampentropy_2 fest_sampentropy_3];
end

样本熵函数：

function saen = SampEntropy( dim, r, data, tau )
% SAMPEN Sample Entropy
%   calculates the sample entropy of a given time series data

%   SampEn is conceptually similar to approximate entropy (ApEn), but has
%   following differences:
%       1) SampEn does not count self-matching. The possible trouble of
%       having log(0) is avoided by taking logarithm at the latest step.
%       2) SampEn does not depend on the datasize as much as ApEn does. The
%       comparison is shown in the graph that is uploaded.

%   dim     : embedded dimension
%   r       : tolerance (typically 0.2 * std)
%   data    : time-series data
%   tau     : delay time for downsampling (user can omit this, in which case
%             the default value is 1)
%

if nargin < 4, tau = 1; end
if tau > 1, data = downsample(data, tau); end

N = length(data);
result = zeros(1,2);

for m = dim:dim+1
    Bi = zeros(1,N-m+1);
    dataMat = zeros(m,N-m+1);

    % setting up data matrix
    for i = 1:m
        dataMat(i,:) = data(i:N-m+i);
    end

    % counting similar patterns using distance calculation
    for j = 1:N-m+1
        % calculate Chebyshev distance, excluding self-matching case
        dist = max(abs(dataMat - repmat(dataMat(:,j),1,N-m+1)));
        % calculate Heaviside function of the distance
        % User can change it to any other function
        % for modified sample entropy (mSampEn) calculation
        D = (dist <= r);
        % excluding self-matching case
        Bi(j) = (sum(D)-1)/(N-m);
    end

    % summing over the counts
    result(m-dim+1) = sum(Bi)/(N-m+1);

end

saen = -log(result(2)/result(1));

end

3.2.5 AR 特征

%% 5.AR
fest_ar = [];
if contains(Featute_time_content,'ar')
ar_order = 8;
fest_ar = zeros(sum(remain_trial),size(Standard_input_data{1,1},1)*ar_order);
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
ar_temp  = [];
ar_temp = aryule(Standard_input_data{trial_loop,sub_loop}',ar_order);
ar_temp = ar_temp(:,2:ar_order+1);
fest_ar(count_trial,:) = reshape(ar_temp',1,size(Standard_input_data{1,1},1)*ar_order);
count_trial = count_trial+1;    
end
end
end

四、时域 特征提取 - 主体函数代码

时域特征主体函数 Festure_candidate_time ：

function [Festure_time,Festure_time_candidate_num]= Festure_candidate_time(Standard_input_data,Featute_time_content,remain_trial)

Festure_time = [];
%% 1.cross_zero
cross_zero = [];
if contains(Featute_time_content,'cross_zero')
cross_zero = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
cross_zero_channel_temp = zeros(1,size(Standard_input_data{1,1},1));
for channel_loop = 1:size(Standard_input_data{1,1},1)
    for point_loop = 1:size(Standard_input_data{1,1},2)-1
    if Standard_input_data{trial_loop,sub_loop}(channel_loop,point_loop) * Standard_input_data{trial_loop,sub_loop}(channel_loop,point_loop+1)<0
    cross_zero_channel_temp(1,channel_loop) = cross_zero_channel_temp(1,channel_loop) + 1;
    end
    end
end
cross_zero(count_trial,:) = cross_zero_channel_temp;   
count_trial = count_trial+1;
end
end
end

%% 2.std
fest_std = [];
if contains(Featute_time_content,'std')
fest_std = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
std_temp  = [];
std_temp  = std(Standard_input_data{trial_loop,sub_loop}');
fest_std(count_trial,:) = std_temp;
count_trial = count_trial+1;    
end
end
end

%% 3.近似熵 
fest_apen = [];
if contains(Featute_time_content,'apen')
r_apen = 0.2*fest_std';    
fest_apen_2 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
fest_apen_3 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;

for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
for channel_loop = 1:size(Standard_input_data{1,1},1)
fest_apen_2(count_trial,channel_loop) = ApEn( 2, r_apen(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
fest_apen_3(count_trial,channel_loop) = ApEn( 3, r_apen(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
end
count_trial = count_trial+1;    
end
end

fest_apen = [fest_apen_2 fest_apen_3];
end

%% 4.样本熵 
fest_sampentropy = [];
if contains(Featute_time_content,'sampentropy')
r_sampentropy = 0.2*fest_std';    
fest_sampentropy_2 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
fest_sampentropy_3 = zeros(sum(remain_trial),size(Standard_input_data{1,1},1));
count_trial = 1;

for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
for channel_loop = 1:size(Standard_input_data{1,1},1)
fest_sampentropy_2(count_trial,channel_loop) = SampEntropy( 2, r_sampentropy(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
fest_sampentropy_3(count_trial,channel_loop) = SampEntropy( 3, r_sampentropy(1,count_trial), Standard_input_data{trial_loop,sub_loop}(channel_loop,:), 1 );
end
count_trial = count_trial+1;    
end
end

fest_sampentropy = [fest_sampentropy_2 fest_sampentropy_3];
end


%% 5.AR
fest_ar = [];
if contains(Featute_time_content,'ar')
ar_order = 8;
fest_ar = zeros(sum(remain_trial),size(Standard_input_data{1,1},1)*ar_order);
count_trial = 1;
for sub_loop = 1:size(remain_trial,2)
for trial_loop = 1:remain_trial(1,sub_loop)
ar_temp  = [];
ar_temp = aryule(Standard_input_data{trial_loop,sub_loop}',ar_order);
ar_temp = ar_temp(:,2:ar_order+1);
fest_ar(count_trial,:) = reshape(ar_temp',1,size(Standard_input_data{1,1},1)*ar_order);
count_trial = count_trial+1;    
end
end
end

%% 时域特征合并
Festure_time = [cross_zero   fest_std    fest_apen    fest_sampentropy   fest_ar];
Festure_time_candidate_num = [size(cross_zero,2)   size(fest_std,2)    size(fest_apen,2)    size(fest_sampentropy,2)   size(fest_ar,2)];
end

---

总结

脑电在时间分辨率的优势，注定其在时域有丰富的潜在特征。
脑电时域特征也从有严谨推导的统计特征，逐步扩展至实用有效地熵类特征。

推荐大家广泛学习时序信号处理的方法，可以移植和创新大量的新算法。
脑电信号作为信号处理的一种，例如阵列信号处理的经典算法都有应用基础。

同时，对经典特征的融合、组合也是发掘更优混合特征的常用方式。
大家可以探索和发掘是用自己研究的优质特征策略。

目前多样性的特征还在不断发展、丰富，新的特征提取方法逐渐多元化。
进阶特征如脑网络、拓扑图等，基于人工智能的端到端特征提取方法，会在新的专栏中介绍。

囿于能力，挂一漏万，如有笔误请大家指正~

---

感谢您耐心的观看，本系列更新了约30000字，约3000行开源代码，体量相当于一篇硕士工作。

往期内容放在了文章开头，麻烦帮忙点点赞，分享给有需要的朋友~

坚定初心，本博客永远：
免费拿走，全部开源，全部无偿分享~

---

To：新想法、鬼点子的道友：

自己：脑机接口+人工智领域，主攻大脑模式解码、身份认证、仿脑模型…
在读博士第3年，在最后1年，希望将代码、文档、经验、掉坑的经历分享给大家~
做的不好请大佬们多批评、多指导~ 虚心向大伙请教！
想一起做些事情 or 奇奇怪怪点子 or 单纯批评我的，请至[email protected]