脑电EEG代码开源分享 【4.特征提取-空域篇】

往期文章

希望了解更多的道友点这里
0. 分享【脑机接口 + 人工智能】的学习之路
1.1 . 脑电EEG代码开源分享 【1.前置准备-静息态篇】
1.2 . 脑电EEG代码开源分享 【1.前置准备-任务态篇】
2.1 . 脑电EEG代码开源分享 【2.预处理-静息态篇】
2.2 . 脑电EEG代码开源分享 【2.预处理-任务态篇】
3.1 . 脑电EEG代码开源分享 【3.可视化分析-静息态篇】
3.2 . 脑电EEG代码开源分享 【3.可视化分析-任务态篇】
4.1 . 脑电EEG代码开源分享 【4.特征提取-时域篇】
4.2 . 脑电EEG代码开源分享 【4.特征提取-频域篇】
4.3 . 脑电EEG代码开源分享 【4.特征提取-时频域篇】
4.4 . 脑电EEG代码开源分享 【4.特征提取-空域篇】
5 . 脑电EEG代码开源分享 【5.特征选择】
6.1 . 脑电EEG代码开源分享 【6.分类模型-机器学习篇】
6.2 . 脑电EEG代码开源分享 【6.分类模型-深度学习篇】
汇总. 专栏：脑电EEG代码开源分享【文档+代码+经验】

0 . 【深度学习】常用网络总结

---

一、前言

本文档旨在归纳BCI-EEG-matlab的数据处理代码，作为EEG数据处理的总结，方便快速搭建处理框架的Baseline，实现自动化、模块插拔化、快速化。本文以任务态（锁时刺激，如快速序列视觉呈现）为例，分享脑电EEG的分析处理方法。
脑电数据分析系列。分为以下6个模块：

1. 前置准备
2. 数据预处理
3. 数据可视化
4. 特征提取（特征候选集）
5. 特征选择（量化特征择优）
6. 分类模型

本文内容：【4. 特征提取-空域篇】

提示：以下为各功能代码详细介绍，若节约阅读时间，请下滑至文末的整合代码

---

二、特征提取 框架介绍

特征提取作为承上启下的重要阶段，是本系列中篇幅最长的部分。承上，紧接预处理结果和可视化分析，对庞大的原始数据进行凝练，用少量维度指标表征整体数据特点；启下，这些代表性、凝练性的特征指标量化了数据性能，为后续的认知解码、状态监测、神经调控等现实需求提供参考。

特征提取的常用特征域为时域、频域、时频域、空域等。本文特征主要为手动设置的经验特征，大多源于脑科学及认知科学的机制结论，提取的特征具有可解释的解剖、认知、物理含义；也有部分是工程人员的实践发现，在模型性能提升中效果显著。

特征提取的代码框图、流程如下所示：

空域特征的主要思路是赋予导联不同权重，关注重要导联对目标任务的作用，其思想很接近目前深度学习中热门的 注意力机制，通过数据驱动的结果导向更新 注意力模块 权重，获得了显著的分类性能提升，相关注意力机制的研究获得了多个顶会的best paper。
拓展阅读：Swin Transformer || VIT

除了 软性的 空间滤波赋予各导联权重，硬性的导联选择更具有显示应用价值。通过选取最重要、评分最高的几个导联，保留留下导联数量的20%甚至更少，对高密度导联进行约减。导联选择的现实意义在于：1.降低了佩戴、安装、准备的操作时间，降低了设备和耗材成本，快速佩戴脑电设备提升了效率，脑电前期准备更加用户友好。 2.导联数量降低有助于减少运算量，同时相应降低特征个数缓解过拟合问题。

空域-特征提取的主要功能，分为以下3部分：

• CSP 共空间模式
• HDCA 分层判别成分分析
• 基于经验的空间特征

1. CSP 共空间模式：将脑电数据按照 导联x数据点 形成矩阵，利用矩阵的对角化变换，通过空间映射将脑电数据映射到距离最远的空间投影上，使得目标和非目标更具有分辨性，便于后期分类器设置判别边界。CSP是脑机接口常用的基础算法，产生了大量以CSP为基础的改进和优化算法，尤其适用于有空间脑区非对称能量差异的任务，如运动想象。
   拓展阅读：CSP原理详解

2. HDCA：强烈推荐的算法，目前个人认为最实用的空域方法之一。hierarchical discriminant component analysis (HDCA) 分层判别成分分析。通过为各通导联、各时间窗内数据赋予权重并且加求和，获得时空加权的HDCA结果。HDCA计算流程为：1.计算导联时间窗中目标与非目标的fisher判别距离，该值越大代表此段时空数据分类效果好。2. fisher值越大则赋予响应导联时间窗权重越大。3.将各导联时间窗内数据 x fisher 权重并求和。HDCA和CSP本质思想相似，都是期望找到目标和非目标样本距离最大的变换方式，CSP使用矩阵变换方法，HDCA使用权重加权的方式。
   fisher判别距离也有称为瑞利熵（Rayleigh entropy），是HDCA赋予各导联、时间窗的依据。其本质思想是量化目标与非目标样本的聚类、离散程度。其主要公式为 不同类间中心距 除以 各自类内的样本距离，类间距使用欧式距离，类内局使用标准差。该结果越大代表此段数据：1. 不同类之间距离较远。2.并且各自类内样本紧凑。对应就是好划定分类边界。
   fisher公式如下：
   
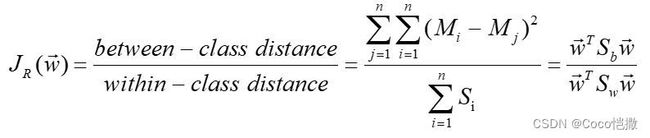
   fisher示意图如下：左侧为易分类脑电样本，右侧为难分类脑电样本
   
   HDCA论文原理图如下：原文链接
   
   HDCA还有较好的升级版SHDCA，引入了滑动模块缓解潜伏期抖动，尤其适用于锁时任务，如P300检测，ERP分析等。个人经验：滑动后因峰值叠加会影响虚警率，并且计算时间大幅增加。大家可以尝试：
   SHDCA原理图如下：原文链接
   
   本文还附上了ROC，AUC等分类指标代码，有兴趣的朋友免费拿走。
   拓展阅读：HDCA原文 || SHDCA原文

3. 基于经验的空间特征：个人经验和神经机制结论是前大数据时代最常用的方法，很多脑区的选择和电极位置的设定都会借鉴前人的经验，个人在研究早期阅读的大量综述类文章至今仍给我巨大帮助，这里默默感谢一下前辈们的研究结果。
   很多实验范式都是相通的，例如运动想象类任务依赖运动区，C3、C4电极要着重关注。SSVEP类编码任务依赖视觉区，枕区Oz、O1、O2。P300检测和ERP类任务依赖顶叶及中线位置电极，Cz、Fz、Pz、C1、C2不可或缺。听觉任务依赖颞叶脑区，T7、T8是常用电极…等等
   P300检测类任务的脑地形图，能量集中在顶叶Cz附近：
   
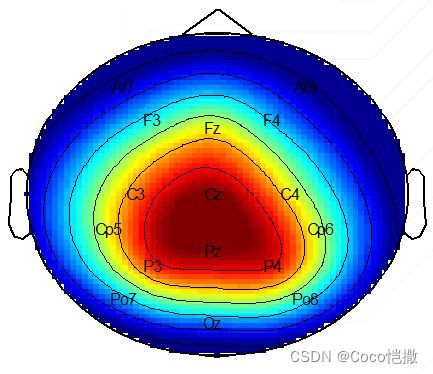
   推荐代码上手困难以及还在入门的朋友们，直接复刻别人的结论和方法是最快最有效途径，这个没有什么不好意思和缺乏创新性，人人都是从模仿前人的脚印过来的，站在前人的台阶会更快有自己的作为。

---

三、代码格式说明

本文非锁时任务态（下文以静息态代替）范例为：ADHD患者、正常人群在静息状态下的脑模式分类

• 代码名称：代码命名为Festure_ candidate_xxx (time / freq/ imf/ space)
• 参数设置：预处理结果\采样率\时域是否非线性熵特征（耗时）\频域均分分辨度\imf阶数\space对比通道数及频带范围。
• 输入格式：输入格式承接规范预处理最后一项输出，Proprocess_xxx(预处理最终步骤)_target/nontarget。
• 输出及保存格式：输出格式为试次数*特征个数，按照除空域特征外，按照通道的特征拼接，先为1通道内的所有特征，接着2通道的所有特征。保存文件名称为Festure_candidate_xxx(特征域名称)_target/nontarget。

---

三、脑电特征提取 代码

提示：代码环境为 matlab 2018

3.0 参数设置

可视化内容可以选择，把希望可视化特征域写在Featute_content 中

• 一次进行10人次的批处理，subject_num = [1;10]
• 特征提取内容： Featute_content = [‘time’,‘freq’,‘time_freq’,‘space’]; 时域、频域、时频域、空域均分析
• 空域特征选择 方法为CSP ：Featute_space_content = [‘csp’];
• CSP中空间滤波器个数为20：space_filter_num = 20;

%% 0.特征候选集-参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data_path = 'C:\Users\EEG\Desktop\basetest_flod\save_fold\';
svae_path = 'C:\Users\EEG\Desktop\basetest_flod\save_fold\';

subject_num = [1;10];

Featute_space_content = ['csp\'];
space_filter_num = 20;

disp(['||特征候选集-参数设置||']);
disp(['特征域内容: ' , Featute_content]);
disp(['时域-候选集: ' , Featute_time_content]);

3.1 标准输入赋值

导入上一步预处理阶段处理后的数据：

%% 1.标准输入赋值
Proprocess_target_file = load([data_path ,'Proprocess_target_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))]);
Proprocess_nontarget_file = load([data_path ,'Proprocess_nontarget_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))]);
stuct_target_name =  'Proprocess_target';
stuct_nontarget_name =  'Proprocess_nontarget';

Proprocess_target_data = Proprocess_target_file.(stuct_target_name).data;
Proprocess_nontarget_data = Proprocess_nontarget_file.(stuct_nontarget_name).data;

subject_num = Proprocess_target_file.(stuct_target_name).subject_num;
fs_down = Proprocess_target_file.(stuct_target_name).fs_down;

remain_trial_target = Proprocess_target_file.(stuct_target_name).remain_trial;
remain_trial_nontarget = Proprocess_nontarget_file.(stuct_nontarget_name).remain_trial;

disp(['目标试次剩余: ' , num2str(remain_trial_target),'||平均： ', num2str(mean(remain_trial_target))]);
disp(['非目标试次剩余: ' , num2str(remain_trial_nontarget),'||平均： ', num2str(mean(remain_trial_nontarget))]);

3.2 空域-特征提取

主函数中 调用空域提取函数

主函数 调用 空域 特征提取函数Festure_candidate_time_freq

%% 5.空域特征候选集
if contains(Featute_content,'space')
disp(['空域特征计算中...']);

tic;
[Festure_space_target,Festure_space_candidate_num_target,Festure_space_nontarget,Festure_space_candidate_num_nontarget]= Festure_candidate_space(Proprocess_target_data,Proprocess_nontarget_data,remain_trial_target,remain_trial_nontarget,Featute_space_content,space_filter_num);
t_space_candidate_cost = toc;
disp(['空域特征计算完毕，耗时(秒)： ',num2str(t_space_candidate_cost)]);

Festure_candidate_space_target = [];
Festure_candidate_space_target.data  = Festure_space_target;
Festure_candidate_space_target.Featute_space_content  = Featute_space_content;
Festure_candidate_space_target.remain_trial_target  = remain_trial_target;
Festure_candidate_space_target.Festure_space_candidate_num_target  = Festure_space_candidate_num_target;
Festure_candidate_space_target.fs_down = fs_down;

Festure_candidate_space_nontarget = [];
Festure_candidate_space_nontarget.data  = Festure_space_nontarget;
Festure_candidate_space_nontarget.Featute_space_content  = Featute_space_content;
Festure_candidate_space_nontarget.remain_trial_nontarget  = remain_trial_nontarget;
Festure_candidate_space_nontarget.Festure_space_candidate_num_nontarget  = Festure_space_candidate_num_nontarget;
Festure_candidate_space_nontarget.fs_down = fs_down;

disp(['空域特征保存中...']);
save([ svae_path , 'Festure_candidate_space_target_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))],'Festure_candidate_space_target');
save([ svae_path , 'Festure_candidate_space_nontarget_',num2str(subject_num(1,1)),'_',num2str(subject_num(2,1))],'Festure_candidate_space_nontarget');
disp(['空域特征保存完毕']);

end

3.3空域特征- CSP（共空间模式）

源代码网址 点击
参考CSP推导 点击

空域 特征提取函数Festure_candidate_time_freq，调用的EMD函数为matlab2018自带

function [Festure_space_target,Festure_space_candidate_num_target,Festure_space_nontarget,Festure_space_candidate_num_nontarget]= Festure_candidate_space(Proprocess_target_data,Proprocess_nontarget_data,remain_trial_target,remain_trial_nontarget,Featute_space_content,space_filter_num)
%% 注：空间特征属于需联合其他特征域的二级特征
%% 注：空间特征一般不处理原始数据，如CSP一般在数据分析后，结合时频的差异性特征，构建时空 or 空频特征

% https://cloud.tencent.com/developer/article/1654056 源代码网址
% CSp的推导 https://blog.csdn.net/MissXy_/article/details/81264953

% 输入参数
% Proprocess_target_data 目标数据（预处理后）
% Proprocess_nontarget_data 非目标数据（预处理后）
% remain_trial_target 目标试次剩余数量
% remain_trial_nontarget 非目标试次剩余数量
% Featute_space_content 空域特征内容
% space_filter_num 一般的CSP特征个数
% 
% 输出参数
% Festure_space_target 目标的空间特征
% Festure_space_candidate_num_target 目标各类的空间特征个数
% Festure_space_nontarget 非目标的非空间特征
% Festure_space_candidate_num_nontarget 非目标各类的空间特征个数

%% 1.数据格式整合
target_3d = [];
trial_count = 1;
for sub_loop = 1:size(Proprocess_target_data,2)
for trial_loop = 1:remain_trial_target(1,sub_loop)
target_3d(:,:,trial_count) = Proprocess_target_data{trial_loop,sub_loop}';
trial_count = trial_count + 1;
end
end

nontarget_3d = [];
trial_count = 1;
for sub_loop = 1:size(Proprocess_nontarget_data,2)
for trial_loop = 1:remain_trial_nontarget(1,sub_loop)
nontarget_3d(:,:,trial_count) = Proprocess_nontarget_data{trial_loop,sub_loop}';
trial_count = trial_count + 1;
end
end

EEG_space_data = cat(3,target_3d,nontarget_3d);
EEG_space_label = [zeros(sum(remain_trial_target),1);ones(sum(remain_trial_nontarget),1)];

%% 2\csp特征计算
if contains(Featute_space_content,'csp')
%check and initializations
EEG_Channels = size(EEG_space_data,2);
EEG_Trials = size(EEG_space_data,3);
classLabels = unique(EEG_space_label);% Return non-repeating values
EEG_Classes = length(classLabels);
covMatrix = cell(EEG_Classes,1); % 协方差矩阵
% Computing the normalized covariance matrices for each trial
trialCov = zeros(EEG_Channels,EEG_Channels,EEG_Trials);
for i = 1:EEG_Trials
    E = EEG_space_data(:,:,i)';
    EE = E*E';
    trialCov(:,:,i) = EE./trace(EE);  % 计算协方差矩阵
end
clear E;
clear EE;
% 计算每一类样本数据的空间协方差之和
for i = 1:EEG_Classes
    covMatrix{i} = mean(trialCov(:,:,EEG_space_label == classLabels(i)),3);
end
% 计算两类数据的空间协方差之和
covTotal = covMatrix{1} + covMatrix{2};
% 计算特征向量和特征矩阵
[Uc,Dt] = eig(covTotal);
% 特征值要降序排列
eigenvalues = diag(Dt);
[eigenvalues,egIndex] = sort(eigenvalues, 'descend');% 降序
Ut = Uc(:,egIndex);
% 矩阵白化
P = diag(sqrt(1./eigenvalues))*Ut';
% 矩阵P作用求公共特征向量transformedCov1 
transformedCov1 = P*covMatrix{1}*P';
%计算公共特征向量transformedCov1的特征向量和特征矩阵
[U1,D1] = eig(transformedCov1);
eigenvalues = diag(D1);
[eigenvalues,egIndex] = sort(eigenvalues, 'descend');% 降序排列
U1 = U1(:, egIndex);
% 计算投影矩阵W
CSPMatrix = U1' * P;
% 计算特征矩阵
% CSP特征选择参数m    CSP特征为2*m个
features_train = zeros(EEG_Trials, 2*space_filter_num+1);
features_test = zeros(EEG_Trials, 2*space_filter_num+1);
Filter = CSPMatrix([1:space_filter_num (end-space_filter_num+1):end],:);
%extracting the CSP features from each trial
for t=1:EEG_Trials    
    %projecting the data onto the CSP filters    
    projectedTrial_train = Filter * EEG_space_data(:,:,t)';    
    %generating the features as the log variance of the projected signals
    variances_train = var(projectedTrial_train,0,2);  
    for f=1:length(variances_train)
        features_train(t,f) = log(variances_train(f));
        % features_train(t,f) = log(variances_train(f)/sum(variances_train));   %修改后对应公式
    end

end
CSP_Train_feature = features_train(:,1:2*space_filter_num);
end



Festure_space_target  = CSP_Train_feature(1:sum(remain_trial_target),:);
Festure_space_candidate_num_target = space_filter_num*2;
Festure_space_nontarget = CSP_Train_feature(1:sum(remain_trial_nontarget),:);
Festure_space_candidate_num_nontarget = space_filter_num*2;

end

3.4 空域特征 - HDCA

3.4.1 HDCA-train

HDCA训练函数

function [w,v,dev,stats]=HDCA_train(w_blocknum,train_data,train_label)
ch=size(train_data,1);

 target_id = find(train_label==1);
 other_id = find(train_label==0);
 tar_num=length(target_id);
 oth_num=length(other_id);

 target_signal=train_data(:,:,target_id);
 other_signal=train_data(:,:,other_id);

%  w_blocknum=floor(size(train_data,2)/fs*40);               %在计算w权重时对波形的分段,即认为1s的数据分为w_blocknum段，每段1000/w_blocknum ms
 w=zeros(ch,w_blocknum);
 num=floor(size(train_data,2)/w_blocknum);          %计算每一分段多少点，要求处下来必须为整数
%  Y_tar_sig=zeros(tar_num,200);
%  Y_oth_sig=zeros(oth_num,200);
 %% 对16导数据进行分块处理
tic
 for i=1:w_blocknum                 %计算每个分段权重，并将16导联数据分段加权到一个信号上
    tar_blockms=target_signal(:,num*(i-1)+1:num*i,:);
    tar_blockms2=mean(tar_blockms,2);        %16导块平均部分
    tar_reshape=reshape(tar_blockms2,ch,tar_num);
    oth_blockms=other_signal(:,num*(i-1)+1:num*i,:);
    oth_blockms2=mean(oth_blockms,2);
    oth_reshape=reshape(oth_blockms2,ch,oth_num); 
    [w(:,i),~]=Fisher(tar_reshape,oth_reshape);
    for t=1:tar_num
        Y_tar_sig(t,num*(i-1)+1:num*i)=(w(:,i)')*tar_blockms(:,:,t);
    end
    for t=1:oth_num
        Y_oth_sig(t,num*(i-1)+1:num*i)=(w(:,i)')*oth_blockms(:,:,t);
    end
 end
 
 %% 取分块间平均值
  v_blocknum=w_blocknum;
 Y_tar_blomean=zeros(tar_num,v_blocknum);
 Y_oth_blomean=zeros(oth_num,v_blocknum);

 for i=1:tar_num
     Y_tar_blomean(i,:)=block_mean(Y_tar_sig(i,:),v_blocknum);
 end
 for i=1:oth_num
    Y_oth_blomean(i,:)= block_mean(Y_oth_sig(i,:),v_blocknum);
 end
%%
% train_data2=cat(1,Y_tar_sig,Y_oth_sig);
% pca_rawdata=reshape(train_data2,tar_num+oth_num,300);
%   [coeff,score1,latent] = pca(pca_rawdata);
%    PcaData=score1(:,1:50)';
%  data=reshape(PcaData,30,tar_num+oth_num);
%%
%  save('BPtrain.mat','Y_tar_blomean','Y_oth_blomean','Y_tar_sig','Y_oth_sig');
 %% 训练时间权重v
% %  [v,b]=Fisher(Y_tar_blomean',Y_oth_blomean');
 train_data=[Y_tar_blomean;Y_oth_blomean];
%  train_data=PcaData;
 train_label=[ones(size(Y_tar_sig,1),1);zeros(size(Y_oth_sig,1),1)];
 [v,dev,stats]=glmfit(train_data,train_label,'binomial','link','logit');

end

3.4.2 HDCA-test

HDCA测试函数

function score=HDCA_test(w_blocknum,w,v,originData)
 allnum=size(originData,3);
 ch=size(originData,1);
%  w_blocknum=size(originData,2)/fs*40;  
 v_blocknum=w_blocknum;
%  % 去中心化
%  for i=1:allnum
%      avgs=mean(originData(:,:,i),2);
%      originData(:,:,i)=originData(:,:,i)-avgs*ones(1,size(originData(:,:,i),2));
%  end
 num=floor(size(originData,2)/w_blocknum);       %计算每一分段多少点，要求处下来必须为整数
%  Y_sig=zeros(allnum,samplerate);
%%
for i=1:w_blocknum                 %计算每个分段权重，并将16导联数据分段加权到一个信号上
    blockms=originData(:,num*(i-1)+1:num*i,:);
    for t=1:allnum
        Y_sig(t,num*(i-1)+1:num*i)=(w(:,i)')*blockms(:,:,t);
    end
end
%%
 Y_blomean=zeros(allnum,v_blocknum);
for i=1:allnum
     Y_blomean(i,:)=block_mean(Y_sig(i,:),v_blocknum);
end


% pca_rawdata=reshape(Y_sig(i,:,:),300,tr_num);
%   [coeff,score1,latent] = pca(Y_sig);
%    Y_blomean=score1(:,1:50);
% score=Y_blomean*v;   %计算兴趣得分
score=glmval(v,Y_blomean,'logit');
%% 
% nontar_id_test=find(test_label==1);
% tar_id_test=find(test_label==2);
% Y_taris = score(tar_id_test,:);
% Y_othis = score(nontar_id_test,:);
end
% AUC
% ROC
% Gg = Gaussian(GF-p);

3.4.3 fisher 线性判别

量化类间距、类内距

function score=HDCA_test(w_blocknum,w,v,originData)
 allnum=size(originData,3);
 ch=size(originData,1);
%  w_blocknum=size(originData,2)/fs*40;  
 v_blocknum=w_blocknum;
%  % 去中心化
%  for i=1:allnum
%      avgs=mean(originData(:,:,i),2);
%      originData(:,:,i)=originData(:,:,i)-avgs*ones(1,size(originData(:,:,i),2));
%  end
 num=floor(size(originData,2)/w_blocknum);       %计算每一分段多少点，要求处下来必须为整数
%  Y_sig=zeros(allnum,samplerate);
%%
for i=1:w_blocknum                 %计算每个分段权重，并将16导联数据分段加权到一个信号上
    blockms=originData(:,num*(i-1)+1:num*i,:);
    for t=1:allnum
        Y_sig(t,num*(i-1)+1:num*i)=(w(:,i)')*blockms(:,:,t);
    end
end
%%
 Y_blomean=zeros(allnum,v_blocknum);
for i=1:allnum
     Y_blomean(i,:)=block_mean(Y_sig(i,:),v_blocknum);
end


% pca_rawdata=reshape(Y_sig(i,:,:),300,tr_num);
%   [coeff,score1,latent] = pca(Y_sig);
%    Y_blomean=score1(:,1:50);
% score=Y_blomean*v;   %计算兴趣得分
score=glmval(v,Y_blomean,'logit');
%% 
% nontar_id_test=find(test_label==1);
% tar_id_test=find(test_label==2);
% Y_taris = score(tar_id_test,:);
% Y_othis = score(nontar_id_test,:);
end
% AUC
% ROC
% Gg = Gaussian(GF-p);

3.4.4 ROC曲线绘制

function [Pd Pf]=ROC( Y_taris,Y_othis)
amin=min(min(Y_othis));
amax=max(max(Y_othis));
middata=(amax-amin)/1e5;
x=[amin:middata:amax];   %x 表示阈值选择范围
Pd=zeros(1,length(x));
Pf=zeros(1,length(x));
for i=1:length(x)
   Pd(i)=length(find((Y_taris>x(i))==1))/length(Y_taris);
   Pf(i)=length(find((Y_othis>x(i))==1))/length(Y_othis);
end
% figure
% plot(Pf,Pd)
% for i=1:length(x)
%    dt(i)=Pd(i)/Pf(i) ;
% end
%   b=x(find(dt==max(dt)));
end

3.4.5 AUC计算

function value = AUC(Pf,Pd)
% 给定Pf，Pd返回对应的AUC值
% s=size(Pf,2);
% value=sum(Pd)*(1/s);
Pf_diff=diff(Pf);
value=abs(sum(Pd(2:end).*Pf_diff));
end

---

总结

脑电头皮上的高密集电极采集了丰富的脑活动信息，
整合全电极后可获得全脑的头皮能量分布。

空域特征从机制研究角度讲，空域特征落在导联位置，实则是电极下的脑功能区，
通过所处位置脑功能区的神经元放电信息，进而了解该脑区在任务中的职能分工。

空域特征会为后期导联选择提供参考，从工程应用角度将，减少密集电极的冗余信息，
挑选效果好的电极着重应用，可以有效降低采集周期并提升分类性能。

同时，对经典特征的融合、组合也是发掘更优混合特征的常用方式。
大家可以探索和发掘是用自己研究的优质特征策略。

目前多样性的特征还在不断发展、丰富，新的特征提取方法逐渐多元化。
进阶特征如脑网络、拓扑图等，基于人工智能的端到端特征提取方法，会在新的专栏中介绍。

囿于能力，挂一漏万，如有笔误请大家指正~

---

---

感谢您耐心的观看，本系列更新了约30000字，约3000行开源代码，体量相当于一篇硕士工作。

往期内容放在了文章开头，麻烦帮忙点点赞，分享给有需要的朋友~

坚定初心，本博客永远：
免费拿走，全部开源，全部无偿分享~

---

To：新想法、鬼点子的道友：

自己：脑机接口+人工智领域，主攻大脑模式解码、身份认证、仿脑模型…
在读博士第3年，在最后1年，希望将代码、文档、经验、掉坑的经历分享给大家~
做的不好请大佬们多批评、多指导~ 虚心向大伙请教！
想一起做些事情 or 奇奇怪怪点子 or 单纯批评我的，请至[email protected]