365天深度学习训练营-第P2周:彩色图片识别
- 本文为365天深度学习训练营 中的学习记录博客
- 参考文章:365天深度学习训练营-第P2周:彩色识别
- 原作者:K同学啊|接辅导、项目定制
目录
- 一、课题背景和开发环境
-
- 开发环境
- 二、前期准备
-
- 1.设置GPU
- 2.导入数据
- 3.数据可视化
- 三、构建简单的CNN网络
-
- 关于矩阵在网络中的大小变化过程的推导结果
- 推导结果2 (`padding=1`时)
- 四、训练模型
-
- 1.设置超参数
- 2.编写训练函数
- 3.编写测试函数
- 4.正式训练
- 五、预测&结果可视化
- 六、模型保存和代码封装
- 七、总结
一、课题背景和开发环境
第P2周:彩色图片识别
- 难度:小白入门⭐
- 语言:Python3、Pytorch
要求:
- 学习如何编写一个完整的深度学习程序
- 手动推导卷积层与池化层的计算过程
本次的重点在于学会构建CNN网络
开发环境
- 电脑系统:Windows 10
- 语言环境:Python 3.8.2
- 编译器:无(直接在cmd.exe内运行)
- 深度学习环境:Pytorch
- 显卡及显存:NVIDIA GeForce GTX 1660 Ti 12G
- CUDA版本:Release 10.0, V10.0.130(
cmd输入nvcc -V或nvcc --version指令可查看)
二、前期准备
1.设置GPU
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import torchvision
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print('Device', device, '\n')
# device(type='cuda')
Device cuda
2.导入数据
使用torchvision.datasets.CIFAR10下载CIFAR10数据集,并划分好训练集与测试集
import os
ROOT_FOLDER = 'data'
CIFAR10_FOLDER = os.path.join(OOT_FOLDER, 'cifar-10-batches-py')
if not os.path.exists(CIFAR10_FOLDER) or not os.path.isdir(CIFAR10_FOLDER):
print('开始下载数据集')
# 下载训练集
train_ds = torchvision.datasets.CIFAR10(ROOT_FOLDER,
train=True,
transform=torchvision.transforms.ToTensor(), # 将数据类型转化为Tensor
download=True)
# 下载测试集
test_ds = torchvision.datasets.CIFAR10(ROOT_FOLDER,
train=False,
transform=torchvision.transforms.ToTensor(), # 将数据类型转化为Tensor
download=True)
else:
print('数据集已下载 直接读取')
# 读取已下载的训练集
train_ds = torchvision.datasets.CIFAR10(ROOT_FOLDER,
train=True,
transform=torchvision.transforms.ToTensor(), # 将数据类型转化为Tensor
download=False)
# 读取已下载的测试集
test_ds = torchvision.datasets.CIFAR10(ROOT_FOLDER,
train=False,
transform=torchvision.transforms.ToTensor(), # 将数据类型转化为Tensor
download=False)
使用torch.utils.data.DataLoader加载数据,并设置batch_size=32
batch_size = 32
# 从 train_ds 加载训练集
train_dl = torch.utils.data.DataLoader(train_ds,
batch_size=batch_size,
shuffle=True)
# 从 test_ds 加载测试集
test_dl = torch.utils.data.DataLoader(test_ds,
batch_size=batch_size)
# 取一个批次查看数据格式
# 数据的shape为:[batch_size, channel, height, weight]
# 其中batch_size为自己设定,channel,height和weight分别是图片的通道数,高度和宽度。
imgs, labels = next(iter(train_dl))
print('Image shape: ', imgs.shape, '\n')
# torch.Size([32, 3, 32, 32]) # 所有数据集中的图像都是32*32的RGB图
Image shape: torch.Size([32, 3, 32, 32])
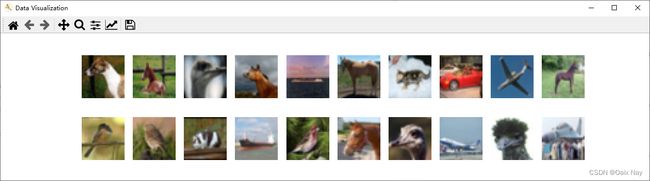
3.数据可视化
import numpy as np
# 指定图片大小,图像大小为20宽、5高的绘图(单位为英寸inch)
plt.figure('Data Visualization', figsize=(20, 5))
for i, imgs in enumerate(imgs[:20]):
# 维度顺序调整 [3, 32, 32]->[32, 32, 3]
npimg = imgs.numpy().transpose((1, 2, 0))
# 将整个figure分成2行10列,绘制第i+1个子图。
plt.subplot(2, 10, i+1)
plt.imshow(npimg, cmap=plt.cm.binary)
plt.axis('off')
三、构建简单的CNN网络
对于一般的CNN网络来说,都是由特征提取网络和分类网络构成,其中特征提取网络用于提取图片的特征,分类网络用于将图片进行分类。
⭐1. torch.nn.Conv2d()详解
函数原型:
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode=‘zeros’, device=None, dtype=None)
参数说明:
- in_channels ( int ) – 输入图像中的通道数
- out_channels ( int ) – 卷积产生的通道数
- kernel_size ( int or tuple ) – 卷积核的大小
- stride ( int or tuple , optional ) – 卷积的步幅。默认值:
1- padding ( int , tuple或str , optional ) – 添加到输入的所有四个边的填充。默认值:
0- padding_mode (字符串,可选) –
'zeros','reflect','replicate'或'circular'。默认:'zeros'
⭐2. torch.nn.Linear()详解
函数原型:
torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)
参数说明:
- in_features:每个输入样本的大小
- out_features:每个输出样本的大小
⭐3. torch.nn.MaxPool2d()详解
函数原型:
torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
参数说明:
- kernel_size:最大的窗口大小
- stride:窗口的步幅,默认值为
kernel_size- padding:填充值,默认为
0- dilation:控制窗口中元素步幅的参数
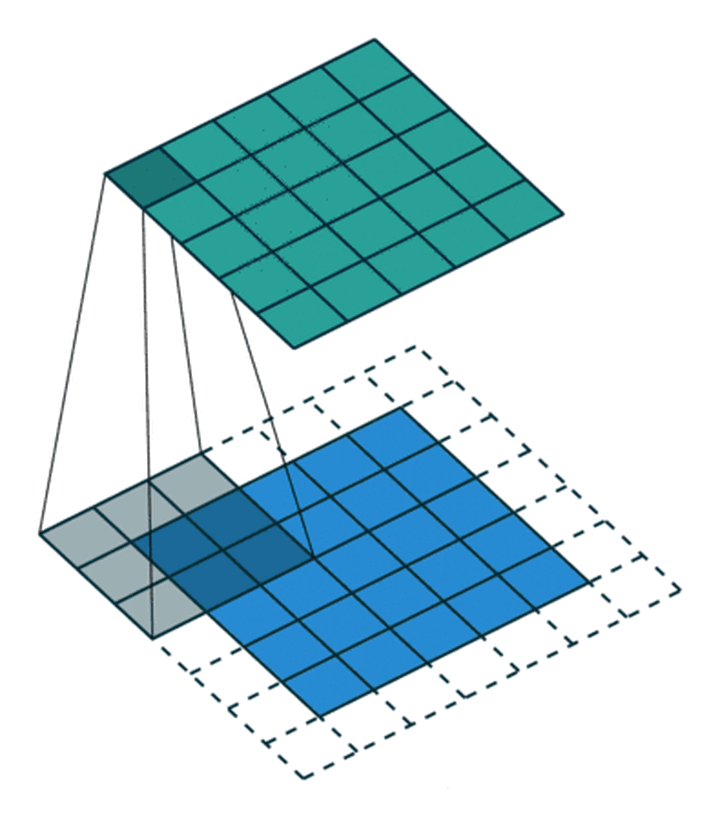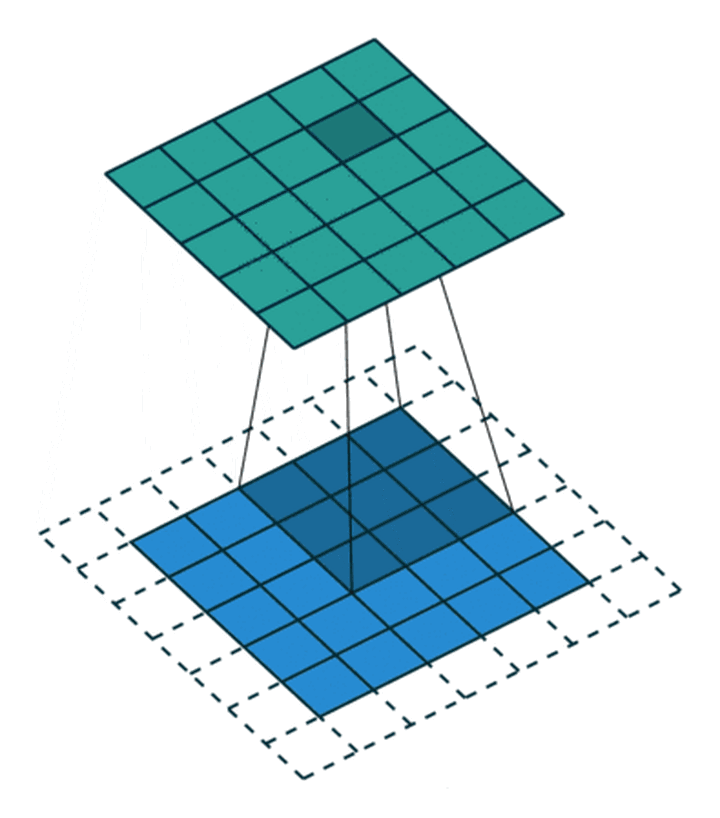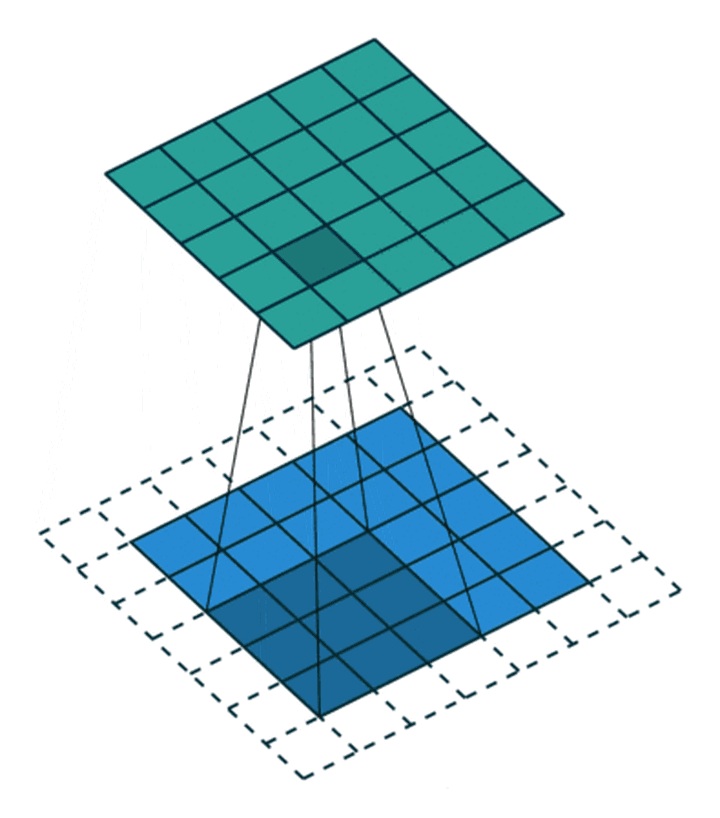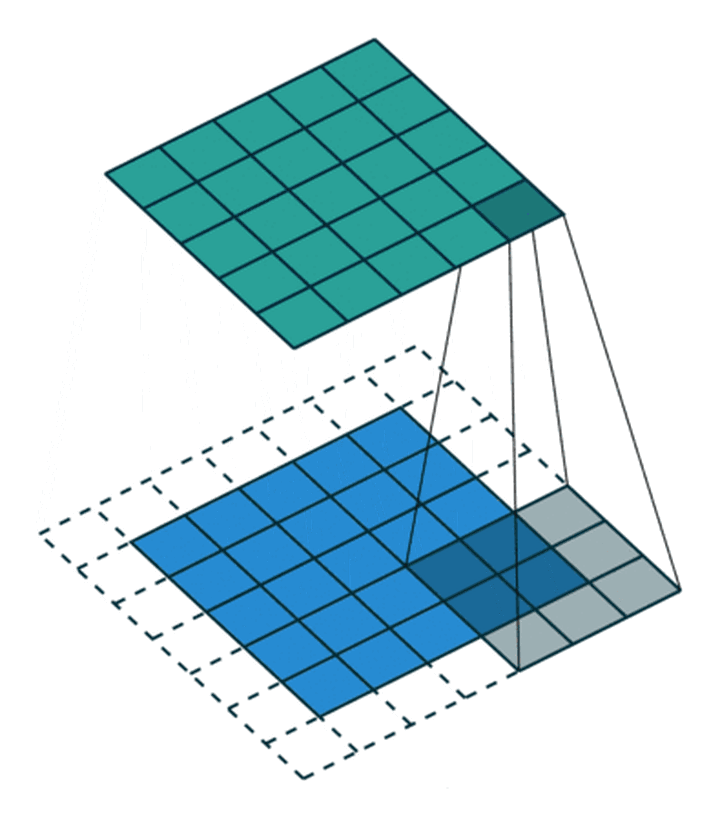
⭐4. 关于卷积层、池化层的计算
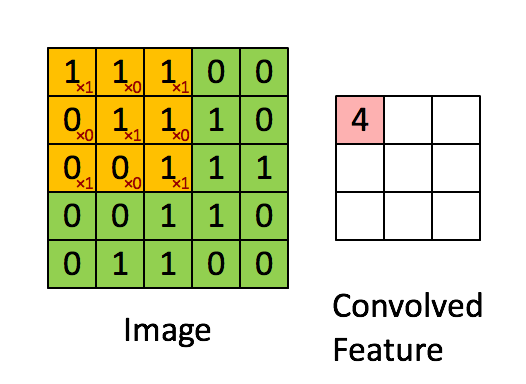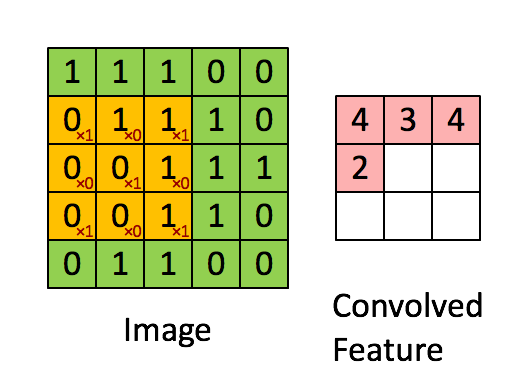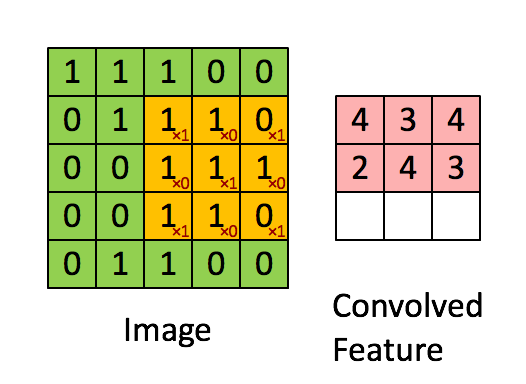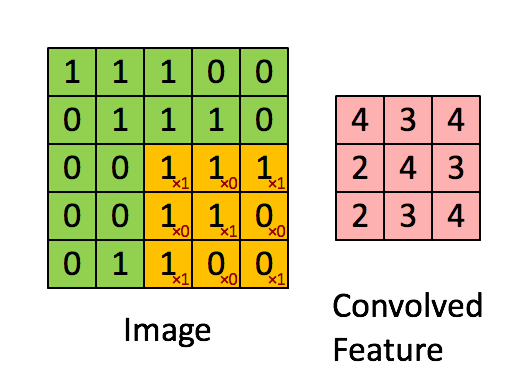
下面是一个简单的卷积过程展示,卷积核大小为3*3:
[[1, 0, 1],
[0, 1, 0],
[1, 0, 1]]
网络数据shape变化过程的推导:
- 符号定义:
input: W 1 × W 2 \ \ \ \ \ W_1 × W_2 W1×W2
kernel: K 1 × K 2 \ \ \ \ K_1 × K_2 K1×K2
padding: P 1 × P 2 \ P_1 × P_2 P1×P2
stride: S 1 × S 2 \ \ \ \ \ S_1 × S_2 S1×S2
dilation: D 1 × D 2 \ \ D_1 × D_2 D1×D2
- 通过卷积层时,shape的变化
⌊ W 1 + P 1 ∗ 2 − ( K 1 − 1 ) − 1 S 1 ⌋ + 1 × ⌊ W 2 + P 2 ∗ 2 − ( K 2 − 1 ) − 1 S 2 ⌋ + 1 \lfloor \frac{W_1 + P_1 * 2 - (K_1 - 1) - 1}{S_1} \rfloor + 1\quad × \quad \lfloor \frac{W_2 + P_2 * 2 - (K_2 - 1) - 1}{S_2} \rfloor + 1 ⌊S1W1+P1∗2−(K1−1)−1⌋+1×⌊S2W2+P2∗2−(K2−1)−1⌋+1- 通过池化层时,shape的变化
⌊ W 1 + P 1 ∗ 2 − ( K 1 − 1 ) ∗ D 1 − 1 S 1 ⌋ + 1 × ⌊ W 2 + P 2 ∗ 2 − ( K 2 − 1 ) ∗ D 2 − 1 S 2 ⌋ + 1 \lfloor \frac{W_1 + P_1 * 2 - (K_1 - 1) * D_1 - 1}{S_1} \rfloor + 1 \quad × \lfloor \quad \frac{W_2 + P_2 * 2 - (K_2 - 1) * D_2 - 1}{S_2} \rfloor + 1 ⌊S1W1+P1∗2−(K1−1)∗D1−1⌋+1×⌊S2W2+P2∗2−(K2−1)∗D2−1⌋+1
- 我的一些理解:
卷积层中的stride过程,类似于在stride=1的卷积基础上再加上了一个核大小等于stride的池化过程
在卷积过程中,如果不设置padding,则矩阵必变小;若需要矩阵大小不变,在不考虑stride的情况下(即stride=1),则需要按照kernel_size大小设置padding的值(例,kernel=3时padding=1,kernel=5时padding=2)。
池化过程本质也是一层卷积,只是把值计算的过程由卷积层中的对应点乘加的计算变为了求最大值(以MaxPool为例)
(上面的公式是我重新推导的,应该没问题)
[参考资料1]
[参考资料2]
构建CNN网络
import torch.nn.functional as F
num_classes = 10 # 图片的类别数
class Model(nn.Module):
def __init__(self):
super().__init__()
# 特征提取网络
self.conv1 = nn.Conv2d(3, 64, kernel_size=3) # 第一层卷积,卷积核大小为3*3
self.pool1 = nn.MaxPool2d(kernel_size=2) # 设置池化层,池化核大小为2*2
self.drop1 = nn.Dropout(p=0.15)
self.conv2 = nn.Conv2d(64, 64, kernel_size=3) # 第二层卷积,卷积核大小为3*3
self.pool2 = nn.MaxPool2d(kernel_size=2) # 设置池化层,池化核大小为2*2
self.drop2 = nn.Dropout(p=0.15)
self.conv3 = nn.Conv2d(64, 128, kernel_size=3) # 第三层卷积,卷积核大小为3*3
self.pool3 = nn.MaxPool2d(kernel_size=2) # 设置池化层,池化核大小为2*2
self.drop3 = nn.Dropout(p=0.15)
# 分类网络
self.fc1 = nn.Linear(512, 256)
self.fc2 = nn.Linear(256, num_classes)
# 前向传播
def forward(self, x):
x = self.drop1(self.pool1(F.relu(self.conv1(x))))
x = self.drop2(self.pool2(F.relu(self.conv2(x))))
x = self.drop3(self.pool3(F.relu(self.conv3(x))))
x = torch.flatten(x, start_dim=1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
加载并打印模型
from torchinfo import summary
# 将模型转移到GPU中(我们模型运行均在GPU中进行)
model = Model().to(device)
summary(model)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
Model --
├─Conv2d: 1-1 1,792
├─MaxPool2d: 1-2 --
├─Dropout: 1-3 --
├─Conv2d: 1-4 36,928
├─MaxPool2d: 1-5 --
├─Dropout: 1-6 --
├─Conv2d: 1-7 73,856
├─MaxPool2d: 1-8 --
├─Dropout: 1-9 --
├─Linear: 1-10 131,328
├─Linear: 1-11 2,570
=================================================================
Total params: 246,474
Trainable params: 246,474
Non-trainable params: 0
=================================================================
我后面用
torch.nn.Sequential把模型重新打包了以下,结构打印出来更清晰一些。
这里设置卷积层的padding=0,如果想要矩阵经过卷积层后大小不改变,在当前kernel_size=3,stride=1的情况下,则需要设置padding=1。
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1=nn.Sequential(
nn.Conv2d(3, 64, kernel_size=3, padding=0),# 64*30*30
nn.ReLU(),
nn.MaxPool2d(2), #高宽减半 64*15*15
nn.Dropout(0.15)
)
self.conv2=nn.Sequential(
nn.Conv2d(64, 64, kernel_size=3, padding=0), # 64*13*13
nn.ReLU(),
nn.MaxPool2d(2), #高宽减半 64*6*6
nn.Dropout(0.15)
)
self.conv3=nn.Sequential(
nn.Conv2d(64, 128, kernel_size=3, padding=0), # 128*4*4
nn.ReLU(),
nn.MaxPool2d(2), #高宽减半 128*2*2
nn.Dropout(0.15)
)
self.fc=nn.Sequential(
nn.Linear(128*2*2, 256),
nn.ReLU(),
nn.Linear(256, num_classes)
)
def forward(self, x):
batch_size = x.size(0)
x = self.conv1(x) # 卷积-激活-池化-Dropout
x = self.conv2(x) # 卷积-激活-池化-Dropout
x = self.conv3(x) # 卷积-激活-池化-Dropout
x = x.view(batch_size, -1) # flatten 变成全连接网络需要的输入 (batch, 128*4*4) ==> (batch, 128*4*4), -1 此处自动算出的是3136
x = self.fc(x)
return x
=================================================================
Layer (type:depth-idx) Param #
=================================================================
ModelS --
├─Sequential: 1-1 --
│ └─Conv2d: 2-1 1,792
│ └─ReLU: 2-2 --
│ └─MaxPool2d: 2-3 --
│ └─Dropout: 2-4 --
├─Sequential: 1-2 --
│ └─Conv2d: 2-5 36,928
│ └─ReLU: 2-6 --
│ └─MaxPool2d: 2-7 --
│ └─Dropout: 2-8 --
├─Sequential: 1-3 --
│ └─Conv2d: 2-9 73,856
│ └─ReLU: 2-10 --
│ └─MaxPool2d: 2-11 --
│ └─Dropout: 2-12 --
├─Sequential: 1-4 --
│ └─Linear: 2-13 131,328
│ └─ReLU: 2-14 --
│ └─Linear: 2-15 2,570
=================================================================
Total params: 246,474
Trainable params: 246,474
Non-trainable params: 0
=================================================================
关于矩阵在网络中的大小变化过程的推导结果
[3, 32, 32](输入数据)
[64, 30, 30](经过卷积层1,k=3,s=1,p=0,则矩阵上下左右各向内缩1px,即长宽均减2)-> [64, 15, 15](经过池化层1,长宽减半)
[64, 13, 13](经过卷积层2)-> [64, 6, 6] (经过池化层2,长宽减半)
[128, 4, 4] (经过卷积层3) -> [128, 2, 2] (经过池化层3,长宽减半)
[512] (flatten拉平) -> [256](FC1层) ->num_classes[10](FC2层)
推导结果2 (
padding=1时)[3, 32, 32](输入数据)
[64, 32, 32](经过卷积层1,k=3,s=1,p=1,则矩阵长宽不变)-> [64, 16, 16](经过池化层1,长宽减半)
[64, 16, 16](经过卷积层2)-> [64, 8, 8] (经过池化层2,长宽减半)
[128, 8, 8] (经过卷积层3) -> [128, 4, 4] (经过池化层3,长宽减半)
[2048] (flatten拉平) -> [256](FC1层) ->num_classes[10](FC2层)
四、训练模型
1.设置超参数
loss_fn = nn.CrossEntropyLoss() # 创建损失函数
learn_rate = 1e-2 # 学习率
opt = torch.optim.SGD(model.parameters(),lr=learn_rate)
2.编写训练函数
optimizer.zero_grad()
loss.backward()
optimizer.step()
关于以上三个函数,我在上一篇文章中有做说明,这里不再赘述
# 训练循环
def train(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset) # 训练集的大小
num_batches = len(dataloader) # 批次数目
train_loss, train_acc = 0, 0 # 初始化训练损失和正确率
for X, y in dataloader: # 获取图片及其标签
X, y = X.to(device), y.to(device)
# 计算预测误差
pred = model(X) # 网络输出
loss = loss_fn(pred, y) # 计算网络输出和真实值之间的差距,targets为真实值,计算二者差值即为损失
# 反向传播
optimizer.zero_grad() # grad属性归零
loss.backward() # 反向传播
optimizer.step() # 每一步自动更新
# 记录acc与loss
train_acc += (pred.argmax(1) == y).type(torch.float).sum().item()
train_loss += loss.item()
train_acc /= size
train_loss /= num_batches
return train_acc, train_loss
3.编写测试函数
测试函数和训练函数大致相同,但是由于不进行梯度下降对网络权重进行更新,所以不需要传入优化器
def test (dataloader, model, loss_fn):
size = len(dataloader.dataset) # 测试集的大小
num_batches = len(dataloader) # 批次数目
test_loss, test_acc = 0, 0
# 当不进行训练时,停止梯度更新,节省计算内存消耗
with torch.no_grad():
for imgs, target in dataloader:
imgs, target = imgs.to(device), target.to(device)
# 计算loss
target_pred = model(imgs)
loss = loss_fn(target_pred, target)
test_loss += loss.item()
test_acc += (target_pred.argmax(1) == target).type(torch.float).sum().item()
test_acc /= size
test_loss /= num_batches
return test_acc, test_loss
4.正式训练
model.train()
model.eval()
关于以上两个个函数,我在上一篇文章中有做说明,这里不再赘述
import time
epochs = 50
train_loss = []
train_acc = []
test_loss = []
test_acc = []
print('\nStart training...')
for epoch in range(epochs):
model.train()
epoch_train_acc, epoch_train_loss = train(train_dl, model, loss_fn, opt)
model.eval()
epoch_test_acc, epoch_test_loss = test(test_dl, model, loss_fn)
train_acc.append(epoch_train_acc)
train_loss.append(epoch_train_loss)
test_acc.append(epoch_test_acc)
test_loss.append(epoch_test_loss)
template = ('Epoch:{:2d}, Train_acc:{:.1f}%, Train_loss:{:.3f}, Test_acc:{:.1f}%,Test_loss:{:.3f}')
print(time.strftime('[%Y-%m-%d %H:%M:%S]'), template.format(epoch+1, epoch_train_acc*100, epoch_train_loss, epoch_test_acc*100, epoch_test_loss))
print('Done')
Start training...
[2022-10-05 14:28:44] Epoch: 1, Train_acc:13.5%, Train_loss:2.269, Test_acc:19.4%,Test_loss:2.177
[2022-10-05 14:28:59] Epoch: 2, Train_acc:24.4%, Train_loss:2.023, Test_acc:26.6%,Test_loss:1.977
[2022-10-05 14:29:12] Epoch: 3, Train_acc:31.6%, Train_loss:1.856, Test_acc:36.0%,Test_loss:1.749
[2022-10-05 14:29:26] Epoch: 4, Train_acc:37.7%, Train_loss:1.693, Test_acc:41.5%,Test_loss:1.608
[2022-10-05 14:29:39] Epoch: 5, Train_acc:42.1%, Train_loss:1.585, Test_acc:42.8%,Test_loss:1.617
[2022-10-05 14:29:53] Epoch: 6, Train_acc:45.5%, Train_loss:1.499, Test_acc:47.0%,Test_loss:1.454
[2022-10-05 14:30:07] Epoch: 7, Train_acc:48.8%, Train_loss:1.418, Test_acc:52.0%,Test_loss:1.341
[2022-10-05 14:30:21] Epoch: 8, Train_acc:51.4%, Train_loss:1.353, Test_acc:51.1%,Test_loss:1.418
[2022-10-05 14:30:35] Epoch: 9, Train_acc:54.1%, Train_loss:1.292, Test_acc:56.4%,Test_loss:1.235
[2022-10-05 14:30:48] Epoch:10, Train_acc:55.4%, Train_loss:1.249, Test_acc:58.5%,Test_loss:1.176
[2022-10-05 14:31:01] Epoch:11, Train_acc:57.4%, Train_loss:1.202, Test_acc:58.1%,Test_loss:1.184
[2022-10-05 14:31:14] Epoch:12, Train_acc:59.0%, Train_loss:1.159, Test_acc:60.6%,Test_loss:1.118
[2022-10-05 14:31:27] Epoch:13, Train_acc:60.3%, Train_loss:1.124, Test_acc:62.1%,Test_loss:1.076
[2022-10-05 14:31:41] Epoch:14, Train_acc:61.6%, Train_loss:1.087, Test_acc:64.3%,Test_loss:1.028
[2022-10-05 14:31:54] Epoch:15, Train_acc:62.8%, Train_loss:1.059, Test_acc:63.6%,Test_loss:1.039
[2022-10-05 14:32:08] Epoch:16, Train_acc:64.1%, Train_loss:1.028, Test_acc:64.8%,Test_loss:1.020
[2022-10-05 14:32:21] Epoch:17, Train_acc:64.8%, Train_loss:1.004, Test_acc:62.4%,Test_loss:1.080
[2022-10-05 14:32:34] Epoch:18, Train_acc:66.0%, Train_loss:0.974, Test_acc:67.9%,Test_loss:0.931
[2022-10-05 14:32:47] Epoch:19, Train_acc:66.9%, Train_loss:0.951, Test_acc:66.5%,Test_loss:0.951
[2022-10-05 14:33:00] Epoch:20, Train_acc:67.1%, Train_loss:0.927, Test_acc:68.8%,Test_loss:0.908
[2022-10-05 14:33:14] Epoch:21, Train_acc:68.6%, Train_loss:0.900, Test_acc:70.0%,Test_loss:0.883
[2022-10-05 14:33:27] Epoch:22, Train_acc:69.1%, Train_loss:0.881, Test_acc:67.6%,Test_loss:0.931
[2022-10-05 14:33:40] Epoch:23, Train_acc:70.0%, Train_loss:0.857, Test_acc:68.9%,Test_loss:0.892
[2022-10-05 14:33:53] Epoch:24, Train_acc:70.9%, Train_loss:0.839, Test_acc:69.8%,Test_loss:0.859
[2022-10-05 14:34:06] Epoch:25, Train_acc:71.5%, Train_loss:0.819, Test_acc:70.3%,Test_loss:0.850
[2022-10-05 14:34:19] Epoch:26, Train_acc:72.1%, Train_loss:0.800, Test_acc:69.0%,Test_loss:0.871
[2022-10-05 14:34:32] Epoch:27, Train_acc:72.4%, Train_loss:0.785, Test_acc:72.2%,Test_loss:0.803
[2022-10-05 14:34:45] Epoch:28, Train_acc:73.1%, Train_loss:0.767, Test_acc:73.3%,Test_loss:0.775
[2022-10-05 14:34:58] Epoch:29, Train_acc:73.8%, Train_loss:0.752, Test_acc:73.5%,Test_loss:0.771
[2022-10-05 14:35:11] Epoch:30, Train_acc:74.0%, Train_loss:0.739, Test_acc:72.2%,Test_loss:0.798
[2022-10-05 14:35:24] Epoch:31, Train_acc:74.6%, Train_loss:0.723, Test_acc:74.1%,Test_loss:0.757
[2022-10-05 14:35:37] Epoch:32, Train_acc:74.9%, Train_loss:0.716, Test_acc:72.0%,Test_loss:0.805
[2022-10-05 14:35:51] Epoch:33, Train_acc:75.4%, Train_loss:0.701, Test_acc:74.4%,Test_loss:0.736
[2022-10-05 14:36:04] Epoch:34, Train_acc:76.1%, Train_loss:0.685, Test_acc:74.8%,Test_loss:0.730
[2022-10-05 14:36:18] Epoch:35, Train_acc:76.3%, Train_loss:0.673, Test_acc:75.0%,Test_loss:0.719
[2022-10-05 14:36:32] Epoch:36, Train_acc:76.7%, Train_loss:0.662, Test_acc:73.5%,Test_loss:0.760
[2022-10-05 14:36:45] Epoch:37, Train_acc:77.1%, Train_loss:0.653, Test_acc:72.8%,Test_loss:0.782
[2022-10-05 14:36:59] Epoch:38, Train_acc:77.7%, Train_loss:0.641, Test_acc:74.1%,Test_loss:0.741
[2022-10-05 14:37:12] Epoch:39, Train_acc:77.9%, Train_loss:0.629, Test_acc:75.7%,Test_loss:0.706
[2022-10-05 14:37:28] Epoch:40, Train_acc:78.2%, Train_loss:0.621, Test_acc:75.4%,Test_loss:0.714
[2022-10-05 14:37:42] Epoch:41, Train_acc:78.3%, Train_loss:0.615, Test_acc:75.7%,Test_loss:0.698
[2022-10-05 14:37:55] Epoch:42, Train_acc:78.9%, Train_loss:0.597, Test_acc:75.9%,Test_loss:0.707
[2022-10-05 14:38:09] Epoch:43, Train_acc:79.0%, Train_loss:0.590, Test_acc:75.5%,Test_loss:0.703
[2022-10-05 14:38:23] Epoch:44, Train_acc:79.5%, Train_loss:0.580, Test_acc:75.3%,Test_loss:0.714
[2022-10-05 14:38:38] Epoch:45, Train_acc:79.9%, Train_loss:0.574, Test_acc:76.4%,Test_loss:0.681
[2022-10-05 14:38:52] Epoch:46, Train_acc:80.4%, Train_loss:0.560, Test_acc:76.5%,Test_loss:0.683
[2022-10-05 14:39:06] Epoch:47, Train_acc:80.6%, Train_loss:0.554, Test_acc:75.1%,Test_loss:0.720
[2022-10-05 14:39:20] Epoch:48, Train_acc:80.6%, Train_loss:0.546, Test_acc:76.5%,Test_loss:0.683
[2022-10-05 14:39:33] Epoch:49, Train_acc:81.0%, Train_loss:0.538, Test_acc:76.0%,Test_loss:0.691
[2022-10-05 14:39:47] Epoch:50, Train_acc:81.2%, Train_loss:0.532, Test_acc:76.6%,Test_loss:0.685
Done
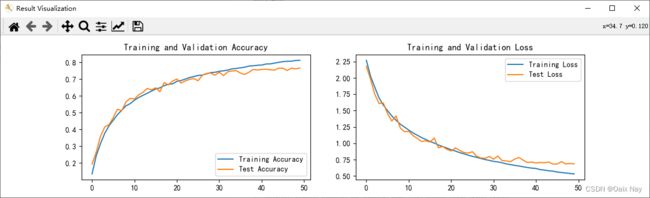
最终结果,训练集准确率达到81.2%,测试集准确率达到76.6%。
五、预测&结果可视化
import matplotlib.pyplot as plt
#隐藏警告
import warnings
warnings.filterwarnings("ignore") #忽略警告信息
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.rcParams['figure.dpi'] = 100 #分辨率
epochs_range = range(epochs)
plt.figure('Result Visualization', figsize=(12, 3))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, train_acc, label='Training Accuracy')
plt.plot(epochs_range, test_acc, label='Test Accuracy')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(1, 2, 2)
plt.plot(epochs_range, train_loss, label='Training Loss')
plt.plot(epochs_range, test_loss, label='Test Loss')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.show()
六、模型保存和代码封装
保存当前模型参数
''' 保存模型参数 '''
saveFile = os.path.join(output, 'epoch'+str(epochs)+'.pkl')
torch.save(model.state_dict(), saveFile)
加载之前保存的模型参数
''' 加载之前保存的模型 '''
if not os.path.exists(output) or not os.path.isdir(output):
os.makedirs(output)
if start_epoch > 0:
resumeFile = os.path.join(output, 'epoch'+str(start_epoch)+'.pkl')
if not os.path.exists(resumeFile) or not os.path.isfile(resumeFile):
start_epoch = 0
else:
model.load_state_dict(torch.load(resumeFile)) # 加载模型参数
最后把代码做了函数封装,大概结构如下:
import os
import time
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchinfo import summary
import matplotlib.pyplot as plt
import numpy as np
import warnings
''' 下载或读取CIFAR10数据集,并划分好训练集与测试集 '''
def getDataset(root, dataset):
pass
''' 加载数据,并设置batch_size '''
def loadData(train_ds, test_ds, batch_size=32, root='', show_flag=False):
pass
''' 数据可视化 '''
def displayData(imgs, root='', flag=False):
pass
''' 构建简单的CNN网络 '''
class Model(nn.Module):
def __init__(self):
pass
def forward(self, x):
pass
''' 训练循环 '''
def train(dataloader, model, loss_fn, optimizer):
pass
''' 测试函数 '''
def test(dataloader, model, loss_fn):
pass
''' 结果可视化 '''
def displayResult(train_acc, test_acc, train_loss, test_loss, start_epoch, epochs, output=''):
pass
if __name__=='__main__':
''' 设置图片的类别数 '''
num_classes = 10
''' 设置GPU '''
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print('Device', device, '\n')
''' 加载数据 '''
root = 'data'
output = 'output'
dataset = os.path.join(root, 'cifar-10-batches-py')
batch_size = 32
train_ds, test_ds = getDataset(root, dataset)
train_dl, test_dl = loadData(train_ds, test_ds, batch_size, dataset, False)
''' 调用并将模型转移到GPU中(我们模型运行均在GPU中进行) '''
model = Model().to(device)
''' 显示网络结构 '''
summary(model)
''' 设置超参数 '''
start_epoch = 0
epochs = 50
learn_rate = 1e-2 # 学习率
loss_fn = nn.CrossEntropyLoss() # 创建损失函数
opt = torch.optim.SGD(model.parameters(),lr=learn_rate)
train_loss = []
train_acc = []
test_loss = []
test_acc = []
''' 加载之前保存的模型 '''
if not os.path.exists(output) or not os.path.isdir(output):
os.makedirs(output)
if start_epoch > 0:
resumeFile = os.path.join(output, 'epoch'+str(start_epoch)+'.pkl')
if not os.path.exists(resumeFile) or not os.path.isfile(resumeFile):
start_epoch = 0
else:
model.load_state_dict(torch.load(resumeFile)) # 加载模型参数
''' 开始训练模型 '''
print('\nStart training...')
for epoch in range(start_epoch, epochs):
model.train()
epoch_train_acc, epoch_train_loss = train(train_dl, model, loss_fn, opt)
model.eval()
epoch_test_acc, epoch_test_loss = test(test_dl, model, loss_fn)
train_acc.append(epoch_train_acc)
train_loss.append(epoch_train_loss)
test_acc.append(epoch_test_acc)
test_loss.append(epoch_test_loss)
template = ('Epoch:{:2d}, Train_acc:{:.1f}%, Train_loss:{:.3f}, Test_acc:{:.1f}%,Test_loss:{:.3f}')
print(time.strftime('[%Y-%m-%d %H:%M:%S]'), template.format(epoch+1, epoch_train_acc*100, epoch_train_loss, epoch_test_acc*100, epoch_test_loss))
print('Done\n')
''' 保存模型参数 '''
saveFile = os.path.join(output, 'epoch'+str(epochs)+'.pkl')
torch.save(model.state_dict(), saveFile)
''' 绘制准确率&损失率曲线图 '''
displayResult(train_acc, test_acc, train_loss, test_loss, start_epoch, epochs, output)
七、总结
总体来讲,这次课题相对上一个课题来讲,难度没太大变化,只是输入数据由上一次的灰度图变成了彩色图像(针对这点,在网络中带来的影响就是第一个卷积层上参数有一点变化)。另外网络相较上一次复杂了一些(增加了一组卷积池化层)。
目前了解到的内容:
- 熟悉了
torch.nn.Sequential接口的使用过程 - 系统的理解了卷积与池化过程,并自己动手跟踪计算了矩阵在网络中每层的变化