新一k

基于强化学习的综合能源系统管理综述-笔记

这篇笔记主要突出强化学习的特点以及于综合能源系统管理上的应用，着重于引出后文的可研究点。具体的方法论文可以参见最后的推荐论文，大都为近年顶刊。

1. 背景

1.1 面临问题

综合能源系统的大规模区域互联使其逐渐发展成为大型高维系统, 间歇性可再生能源和包含电动汽车(Electric vehicle, EV)、分布式储能设备在内的柔性负载的接入增加了综合能源系统的复杂动态特性, 另外用户能源消耗行为的随机性、能源多样性和不同形式能源之间的耦合关系也给现代化能源管理带来了巨大的挑战。混合整数规划、线性规划、非线性规划等传统优化算法往往依赖于精确的数学模型和参数, 考虑到综合能源系统是具有高度不确定性的复杂动态系统, 精确的模型构造十分困难, 因此传统优化算法在求解综合能源系统管理问题中的应用受到限制。

1.2 强化学习

1.2.1 简单介绍

（1）强化学习不需要监督信号来直接指导学习，只依赖于一个反馈回报信号，对其“试错”过程进行评估，间接指导智能体向反馈回报值最大的方向进行学习，从而较少对精确的系统模型的依赖。强化学习在马尔科夫决策过程中主要使用的方法包括自适应动态规划 (Adaptive dynamic programming, ADP)、时间差分 (Temporal difference, TD) 学习、蒙特卡洛法 (Monte carlo, MC) 等。

针对综合能源系统的变量高维度特性，强化学习可以采用多层马尔科夫决策过程 (Markov decision process, MDP) 模型进行分层优化；
在面对一些具有连续动作和状态空间的问题时, 强化学习还可以与具有出色数据处理能力的深度学习相结合构成深度强化学习算法 (Deep reinforcement learning, DRL)，进而求解得到具有高维变量的综合能源系统的最优管理策略，并且该方法相较于传统优化方法在实际生活场景下更容易实现。

（2）根据学习方式的不同, 强化学习可以分为在线策略和离线策略：

在线策略是指生成样本的策略与网络更新参数时使用的策略不同，即与环境互动和网络更新同时进行，一边采样一边更新。
离线策略则是指生成样本的策略与网络更新参数时使用的策略相同，采用先采样后集中更新的方式进行学习。两者的本质区别在于，更新 Q 值的方法是沿用既定策略还是新策略。

（3）根据动作的选择依据，强化学习又可以分为基于价值的强化学习和基于策略的强化学习：

基于价值的强化学习是在知晓所有动作价值的基础上，根据最高价值来选择动作，因此并不适用于选取连续动作。
基于策略的强化学习则是通过对环境的分析，直接输出下一步可能采取的各种动作的概率，然后根据概率采样选取行动。

（4）根据模型是否完全给定，强化学习还可以分为基于模型的强化学习和无模型的强化学习。

基于模型的强化学习依赖于环境在各个动作下的状态转移概率。
无模型的方法不需要完整的环境信息, 当给予适当的奖励时智能体可以自主学习最优策略。

1.2.2 面临挑战

（1）挑战：如何平衡探索与开发、如何处理高维决策问题、如何减小状态动作价值的估计误差、如何提升学习效率等。

（2）如何平衡探索与开发？

定义：
- 探索：指尝试之前没有执行过的动作以期望获得超过当前最优动作的奖励回报；
- 开发：指执行已经学习到的能获得最大奖励回报的动作, 即贪婪动作。
方法：
- $\epsilon$ -贪婪策略：智能体在每个状态有 $1-\epsilon$ 的概率选择进行开发，有 $\epsilon$ 的概率进行探索。当动作空间为 $A$ 时， $∣ A ∣$ 是该空间中的动作总数，除贪婪动作外各个动作被采取的概率为 $\epsilon/(|A|-1)$ 。
- 添加随机噪声：使得采取的动作是在贪婪动作邻域内随机探索的结果。

（3）如何处理高维决策问题？

深度强化学习：深度学习中深度神经网络从高维数据中提取低维特征，能够有效解决维度灾害，再与强化学习相结合，解决具有高维状态和动作空间的序列决策问题。
常见算法：深度 Q 网络 (Deep Q network，DQN)、演员-评论家算法 (Actor-Critic，AC)等。
- 针对 Q 值被高估的问题, 提出了深度双 Q 网络 (Double deep Q network, Double DQN), 通过解耦动作的选择和目标 Q 值的计算, 来解决过度估计问题, 提升算法性能。
  
  深度竞争 Q 网络 (Dueling deep Q network, Dueling DQN) 也能提高估计值的精确度, 提升算法稳定性。
- 针对在连续动作空间的动作选取，提出了演员-评论家算法，该算法融合了以状态动作价值为基础 (比如 Q 学习) 和以动作概率为基础 (比如策略梯度) 的两类强化学习算法。
  
  基于AC算法的改进算法：优势演员-评论家算法 (Advantage actorcritic, A2C)、异步优势演员-评论家算法 (Asynchronous advantage actor-critic, A3C)、置信域策略梯度算法 (Trust region policy optimization,TRPO)、近端策略优化算法 (Proximal policy optimization, PPO)、深度确定性策略梯度算法(Deep deterministic policy gradient, DDPG)。

2. 基于强化学习的电力系统管理

2.1 微电网管理

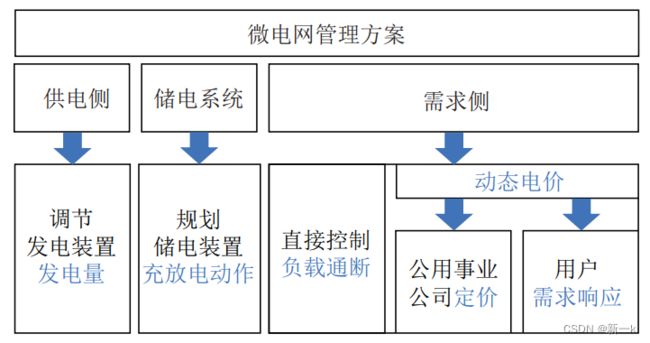
微电网是集成了分布式电源、储电系统、电能转换设备和用电负载的小型配电系统。在微电网电能优化管理中, 优化变量主要包括电力交易价格、功率分配方案等, 优化目标包括最大化运营商收益、最小化购电成本、提高用户用电满意度、减少能量传输损失、提高新能源利用率、提高系统稳定性等。如图 2-1 所示，对微电网实施能源优化管理主要从供电侧、储电系统和需求侧三个方面进行考虑。

图2-1 微电网管理方案

基于强化学习的微电网管理，可以从时间尺度、管理方案和求解算法三个角度进行总结，并可以从收敛稳定性、计算速度、隐私保护和适应性4个方面分析这些算法的性能。

时间尺度：日前调度、日内滚动优化和实时调整。
管理方案：公用事业公司定价、储电装置调节、消费者价格感知等。
求解方法：自适应强化学习、深度确定性策略梯度、有限时域深度确定性策略梯度、有限时域递归确定性策略梯度等。

2.2 智能家庭电能优化管理

（略）

2.3 电动汽车充放电策略管理

（略）

3. 基于强化学习的综合能源系统管理

3.1 能源系统

综合能源系统：以电力为核心, 耦合了燃气、热力及其他能源的综合能源系统。

具有多元大数据、源荷双端不确定、时空多维耦合等特征。
能源互联网（Energy Internet, EI）:以电力网络、热力网络、天然气网络及交通网络等复杂网络为物理实体的一种新型开放式能源生态系统。
自能源（We-energy）:是能够实现能量间双向传输及灵活转换的能源互联网子单元。

3.2 综合能源系统管理

（1）优化目标

经济角度：主要包括系统建设运行维护成本、能源消费成本和能源利用率。
社会角度：包括降低能耗峰均比、平整负荷曲线提升能源网络稳定性、提升用户满意度以及环境友好性。

（2）求解方法

传统算法：混合整数线性规划、混合整数非线性规划、博弈论、合作博弈论、交替方向乘子法、混合整数二阶锥规划交替方向乘子法、基于多目标粒子群优化的双层元启发式算法等。
强化学习：深度确定性策略梯度、置信域策略梯度算法+深度确定性策略梯度、多智能体议价学习 + 强化学习、深度双神经拟合Q迭代、演员-评论家算法等。

（3）强化学习求解性能分析

优点：
- 分层马尔科夫决策过程是一种求解具有高维变量问题的思路，而且能一定程度上保护用户隐私信息，适用于有隐私保护需求的高维综合能源系统管理优化问题。
- 不具有模型依赖性，可以在没有先验知识的情况下通过与环境交互进行学习，解决新能源发电和用户用能需求的不确定性带来的问题，同时深度神经网络的引入还可以解决维度灾难和复杂优化变量耦合的问题。
缺点：
- 学习性能较依赖人为设置的奖励函数；
- 可解释性低；
- 奖励函数还需要适用于不同种类能源和具有不同特性用能设备学习，设计存在一定困难。

4. 可科研点

（1）多时间尺度特性

日前调度虽然计算相对比较简单，但由于时间尺度较大，而且综合能源系统存在较大的不确定性，在对综合能源系统的实际管理中计划情况可能会与实际情况发生较大偏差，导致优化效果不佳. 因此考虑更为复杂的日内滚动优化、实时调整或者三者相互结合的多时间尺度优化，这样能更加准确地对实际情况进行预估。

（2）可解释性

由于在面对一些具有连续动作和状态空间的综合能源系统管理问题时引入了深度学习，用数据驱动的神经网络来拟合策略函数、值函数; 在面对新能源发电和用户耗能需求不确定性时，一些基于强化学习的方法也用到深度网络对不确定因素进行预测，这都使强化学习在能源管理问题中的可解释性受到一定程度的影响。因此，如何提升深度强化学习的可解释性是未来深度强化学习方法应用于实际综合能源系统管理中要面临的一个重要问题。

（3）迁移性

深度学习具有严重的数据依赖性，加速学习过程是强化学习方法面临的一个重要问题。在机器学习中, 迁移学习作为一种运用相似任务已经训练好的网络中包含的知识来求解目标任务的方法，主要思想为: 解决类似任务的知识会加速目标任务的学习过程，并且在类似任务数据充足的前提下有效降低对目标任务的数据依赖。

针对经常发生变化的综合能源系统管理问题，进一步可以考虑使用元学习。元学习通过研究如何让神经网络充分利用旧的综合能源系统中获得的知识经验来指导新系统中的学习任务，使得神经网络能针对新系统的能源管理任务进行适当调整，从而具有学会学习的能力。一个好的元学习模型能够很好地推广到从未遇到过的新的综合能源系统管理场景中，最终经过模型的自我调整可以完成新的综合能源系统管理任务。其中小样本学习是元学习的一种典型方法，可以克服综合能源系统中数据样本少的困难，并降低数据采集成本。此外，元学习还可以与强化学习结合构成元强化学习，减少强化学习方法对超参数、策略网络参数、奖励函数等的依赖。基于此，未来在综合能源系统管理优化问题中，可以通过迁移学习、小样本学习甚至元学习与深度强化学习相结合来解决迁移性的问题，同时克服数据依赖并加快学习过程。

（4）信息安全性

随着智能电表和智能设备的发展，人们的用电偏好和习惯包含在用户数据信息中，可以随时被获取，如何掩盖这些信息成为新的研究热点。由于在处理具有不完全信息的优化问题中的突出表现，强化学习方法在不需要新能源发电和用户用能数据的情况下，通过与环境交互获得的奖励回报中学习到最优能源管理策略，一定程度上保护了用户隐私信息，提升信息安全性。

未来能源管理中多时间尺度特性、可解释性、迁移性和信息安全性的问题将得到人们越来越多的重视, 相应的多时间尺度优化、机理知识与数据驱动相融合的方法以及迁移学习、元学习等算法也将与强化学习算法相结合, 用于综合能源系统管理优化问题。