机器学习总结

均值、中值和众数

从一组数字中我们可以学到什么？

在机器学习（和数学）中，通常存在三中我们感兴趣的值：

• 均值（Mean） - 平均值
• 中值（Median） - 中点值，又称中位数
• 众数（Mode） - 最常见的值

例如：我们已经登记了 13 辆车的速度：

speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]

什么是平均，中间或最常见的速度值？

均值

均值就是平均值。

要计算平均值，请找到所有值的总和，然后将总和除以值的数量：

(99+86+87+88+111+86+103+87+94+78+77+85+86) / 13 = 89.77

中值

中值是对所有值进行排序后的中间值：

77, 78, 85, 86, 86, 86, 87, 87, 88, 94, 99, 103, 111

在找到中位数之前，对数字进行排序很重要。

众数

众值是出现次数最多的值

标准差

什么是标准差

标准差（又常称均方差）是一个数字，描述值的离散程度。

低标准偏差表示大多数数字接近均值（平均值）。

高标准偏差表示这些值分布在更宽的范围内。

例如：这次我们已经登记了 7 辆车的速度：

speed = [86,87,88,86,87,85,86]

标准差是：0.9

方差

方差是另一种数字，指示值的分散程度。

实际上，如果采用方差的平方根，则会得到标准差！

或反之，如果将标准偏差乘以自身，则会得到方差！

标准差

计算标准差的公式是方差的平方根：

√ 1432.25 = 37.85

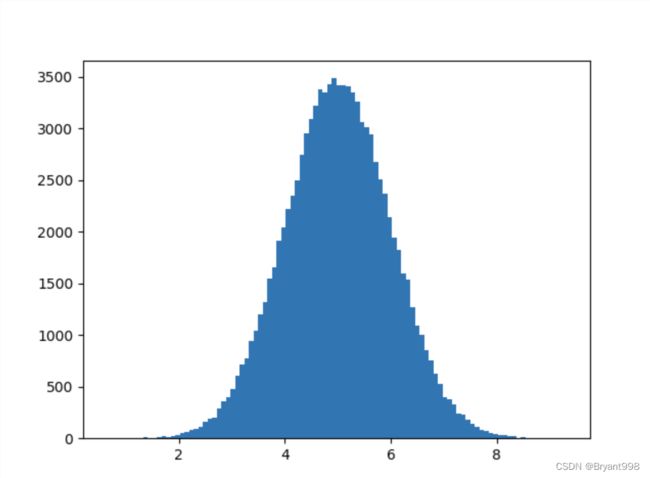
正态数据分布

 

 

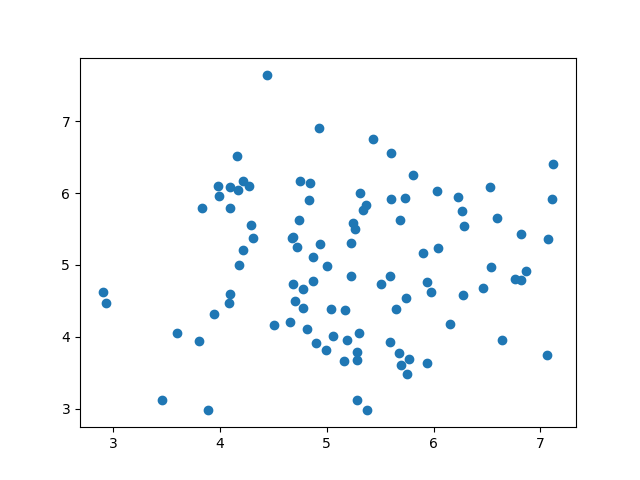
散点图（Scatter Plot）

散点图是数据集中的每个值都由点表示的图。

Matplotlib 模块有一种绘制散点图的方法，它需要两个长度相同的数组，一个数组用于 x 轴的值，另一个数组用于 y 轴的值：

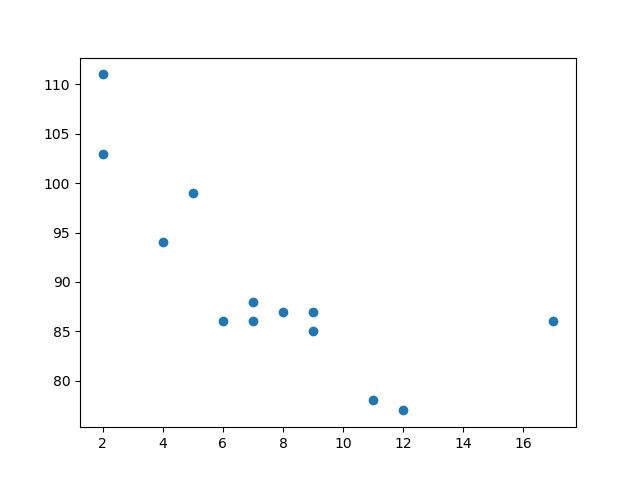
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]

y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x 数组代表每辆汽车的年龄。

y 数组表示每个汽车的速度。

实例

请使用 scatter() 方法绘制散点图：

import matplotlib.pyplot as plt

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

plt.scatter(x, y)
plt.show()

结果：

运行实例

散点图解释

x 轴表示车龄，y 轴表示速度。

从图中可以看到，两辆最快的汽车都使用了 2 年，最慢的汽车使用了 12 年。

注释：汽车似乎越新，驾驶速度就越快，但这可能是一个巧合，毕竟我们只注册了 13 辆汽车。

随机数据分布

在机器学习中，数据集可以包含成千上万甚至数百万个值。

测试算法时，您可能没有真实的数据，您可能必须使用随机生成的值。

正如我们在上一章中学到的那样，NumPy 模块可以帮助我们！

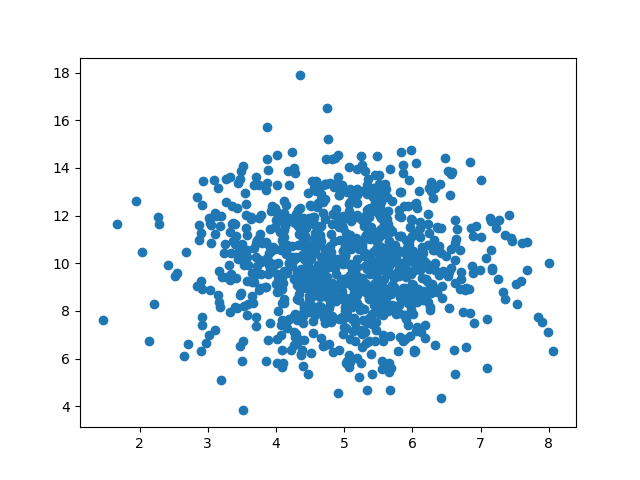
让我们创建两个数组，它们都填充有来自正态数据分布的 1000 个随机数。

第一个数组的平均值设置为 5.0，标准差为 1.0。

第二个数组的平均值设置为 10.0，标准差为 2.0：

实例

有 1000 个点的散点图：

import numpy
import matplotlib.pyplot as plt

x = numpy.random.normal(5.0, 1.0, 1000)
y = numpy.random.normal(10.0, 2.0, 1000)

plt.scatter(x, y)
plt.show()

结果：

 

线性回归

线性回归使用数据点之间的关系在所有数据点之间画一条直线。

这条线可以用来预测未来的值。

在机器学习中，预测未来非常重要。

工作原理

Python 提供了一些方法来查找数据点之间的关系并绘制线性回归线。我们将向您展示如何使用这些方法而不是通过数学公式。

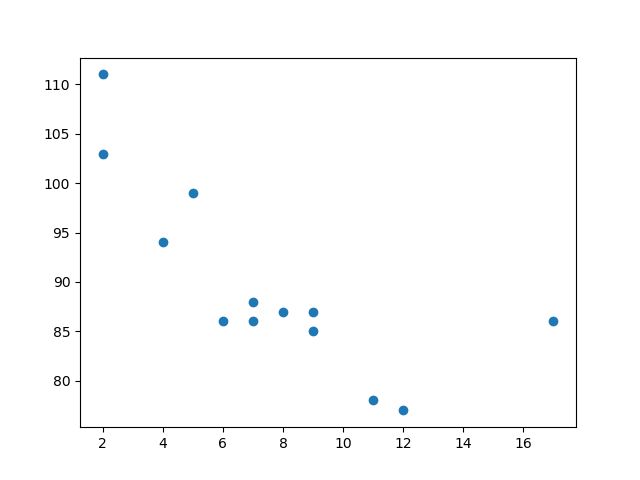
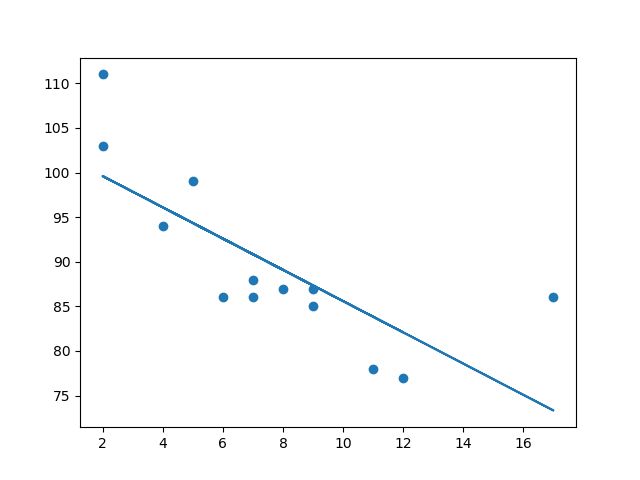
在下面的示例中，x 轴表示车龄，y 轴表示速度。我们已经记录了 13 辆汽车通过收费站时的车龄和速度。让我们看看我们收集的数据是否可以用于线性回归：

实例

首先绘制散点图：

import matplotlib.pyplot as plt

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

plt.scatter(x, y)
plt.show()

结果：

运行实例

实例

导入 scipy 并绘制线性回归线：

import matplotlib.pyplot as plt
from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
  return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

结果：

决策树：