什么是批标准化 (Batch Normalization)

什么是批标准化 (Batch Normalization)

每层都做标准化

你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；再也不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，搞视觉的估计比较熟悉），因为BN本身就是一个归一化网络层。

BN概述

就像激活函数层、卷积层、全连接层、池化层一样，BN(Batch Normalization)也属于网络的一层。在前面我们提到网络除了输出层外，其它层因为低层网络在训练的时候更新了参数，而引起后面层输入数据分布的变化。这个时候我们可能就会想，如果在每一层输入的时候，再加个预处理操作那该有多好啊，比如网络第三层输入数据X3(X3表示网络第三层的输入数据)把它归一化至：均值0、方差为1，然后再输入第三层计算，这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。
而事实上，paper的算法本质原理就是这样：**在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。**不过文献归一化层，可不像我们想象的那么简单，它是一个可学习、有参数的网络层。既然说到数据预处理，最强的预处理方法：白化。
预处理操作选择
说到神经网络输入数据预处理，最好的算法莫过于白化预处理。然而白化计算量太大了，很不划算，还有就是白化不是处处可微的，所以在深度学习中，其实很少用到白化。经过白化预处理后，数据满足条件：a、特征之间的相关性降低，这个就相当于pca；b、数据均值、标准差归一化，也就是使得每一维特征均值为0，标准差为1。如果数据特征维数比较大，要进行PCA，也就是实现白化的第1个要求，是需要计算特征向量，计算量非常大，于是为了简化计算，作者忽略了第1个要求，仅仅使用了下面的公式进行预处理，也就是近似白化预处理：

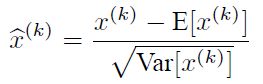
公式简单粗糙，但是依旧很牛逼。因此后面我们也将用这个公式，对某一个层网络的输入数据做一个归一化处理。需要注意的是，我们训练过程中采用batch 随机梯度下降，上面的E(xk)指的是每一批训练数据神经元xk的平均值；然后分母就是每一批数据神经元xk激活度的一个标准差了。

BN算法

经过前面简单介绍，这个时候可能我们会想当然的以为：好像很简单的样子，不就是在网络中间层数据做一个归一化处理嘛，这么简单的想法，为什么之前没人用呢？然而其实实现起来并不是那么简单的。其实如果是仅仅使用上面的归一化公式，对网络某一层A的输出数据做归一化，然后送入网络下一层B，这样是会影响到本层网络A所学习到的特征的。打个比方，比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制把它给我归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，这可怎么办？于是文献使出了一招惊天地泣鬼神的招式：变换重构，引入了可学习参数γ、β，这就是算法关键之处：

每一个神经元xk都会有一对这样的参数γ、β。这样其实当：

是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是：

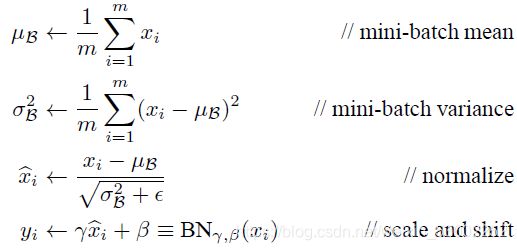
上面的公式中m指的是mini-batch size。
Batch Normalization，简称BatchNorm或BN，翻译为“批归一化”，是神经网络中一种特殊的层，如今已是各种流行网络的标配。在原paper中，BN被建议插入在（每个）ReLU激活层前面，如下所示，

Batch Normalization的正确打开方式:

Batch Normalization在TensorFlow中有三个接口调用 (不包括slim、Keras模块中的)，分别是：

• tf.layers.batch_normalization
• tf.nn.batch_normalization
• tf.contrib.layers.batch_norm
  通过观察这三个接口的参数列表可以得到一个初步的结论，tf.layers.batch_normalization和tf.contrib.layers.batch_norm可以用来构建待训练的神经网络模型，而tf.nn.batch_normalization一般只用来构建推理模型。简洁起见，本文把神经网络模型分为训练模式和推理模式（包括推理、测试和评估等）。由于tf.contrib包的不稳定性，本文将主要介绍如何使用tf.layers.batch_normalization这个方法在模型中添加BN layer。

tf.layers.batch_normalization()方法

方法接口如下：

tf.layers.batch_normalization(
    inputs,
    axis=-1,
    momentum=0.99,
    epsilon=0.001,
    center=True,
    scale=True,
    beta_initializer=tf.zeros_initializer(),
    gamma_initializer=tf.ones_initializer(),
    moving_mean_initializer=tf.zeros_initializer(),
    moving_variance_initializer=tf.ones_initializer(),
    beta_regularizer=None,
    gamma_regularizer=None,
    beta_constraint=None,
    gamma_constraint=None,
    training=False,
    trainable=True,
    name=None,
    reuse=None,
    renorm=False,
    renorm_clipping=None,
    renorm_momentum=0.99,
    fused=None,
    virtual_batch_size=None,
    adjustment=None
)

这里有几个重要参数需要注意：

• axis的值取决于按照input的哪一个维度进行BN，例如输入为channel_last format，即[batch_size, height, width, channel]，则axis应该设定为4，如果为channel_first format，则axis应该设定为1.
• momentum的值用在训练时，滑动平均的方式计算滑动平均值moving_mean和滑动方差moving_variance。 后面做更详细的说明。
• center为True时，添加位移因子beta到该BN层，否则不添加。添加beta是对BN层的变换加入位移操作。注意，beta一般设定为可训练参数，即trainable=True。
• scale为True是，添加缩放因子gamma到该BN层，否则不添加。添加gamma是对BN层的变化加入缩放操作。注意，gamma一般设定为可训练参数，即trainable=True。
• training表示模型当前的模式，如果为True，则模型在训练模式，否则为推理模式。要非常注意这个模式的设定，这个参数默认值为False。如果在训练时采用了默认值False，则滑动均值moving_mean和滑动方差moving_variance都不会根据当前batch的数据更新，这就意味着在推理模式下，均值和方差都是其初始值，因为这两个值并没有在训练迭代过程中滑动更新。

TensorFlow中模型训练时的梯度计算、参数优化等train_op并没有依赖滑动均值moving_mean和滑动方差moving_variance，则moving_mean和moving_variance不会自动更新，所以必须加入负责更新这些参数的update_ops到依赖中，且应该在执行前向计算结束后、后向计算开始前执行update_ops，所以添加依赖的位置不能出错。实际中，只需要在构建模型代码中，添加完所有BN层之后获取update_ops就不会出错，切记！切记！这是TensorFlow的图计算模式造成的编程影响，在其他深度学习框架中可能会有差别。

BN算法用大白话描述就是，计算出当前batch的每个channel的均值mean，计算出当前batch的每个channel的方差variance，令输入减去均值再除以标准差delta，得到normalized输出x-hat，最后乘以scale参数gamma，加上shift参数beta，得到最终变换后的输出y。

BN层在train与inference时的差别：
在训练时，我们可以计算出batch的均值和方差，迭代训练过程中，均值和方差一直在发生变化。但是在推理时，均值和方差是固定的，它们在训练过程中就被确定下来。《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》中给出的确定方式和TensorFlow中存在不同，这里我们介绍TensorFlow中的方式，即采用滑动平均MovingAverage的方法，公式为: moving_average_value * momentum + value * (1 - momentum)，其中value为当前batch的平均值或方差，moving_average_value为滑动均值或滑动方差。
最终，模型训练完毕后，在推理时使用滑动平均值moving_mean和滑动方差moving_variance对feature maps进行变换。

具体可查就看：
https://www.jianshu.com/p/437fb1a5823e