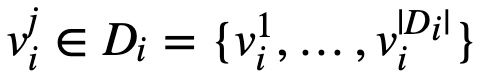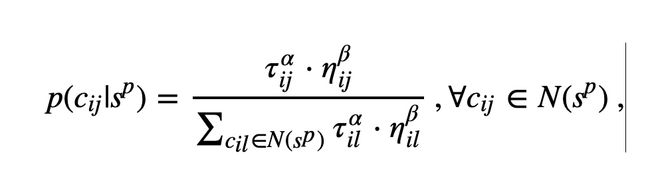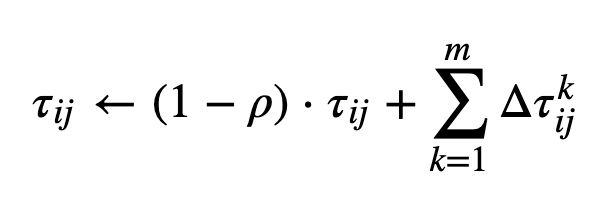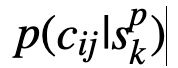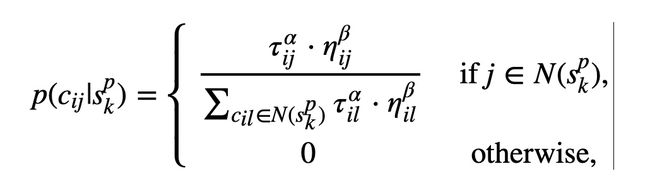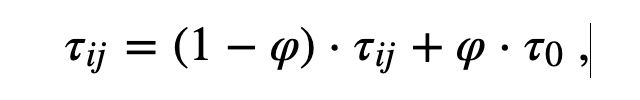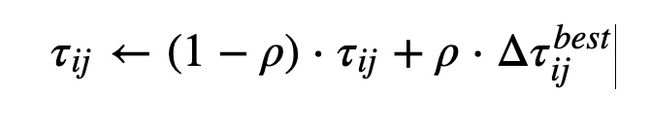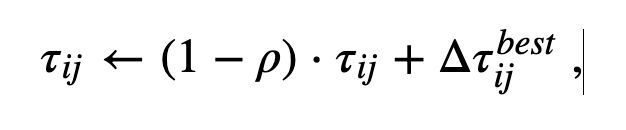蚁群算法详解讲解

0x01 蚁群效应

《昆虫记》中这样描述红蚂蚁：
红蚂蚁出征的远近取决于黑蚂蚁家的远近，它们出征的道路并不选择，也没有明确的目的地。除了水路之外，它们都能穿过

单个蚂蚁不存在有规律的、复杂的行为体系，较大的不确定性和随机性使单个蚂蚁不具备训练条件，一个庞大的蚁群可以看作一个完备的系统，分工明确，行为轨迹可分析，蚁群效应主要用于管理层面，蚁群具有明确分工和严谨的组织框架

但蚁群算法使用的分析结构和蚁群效应不同

0x02 Traveling salesman problem

在理解蚁群算法时，可以以旅行推销员问题（Traveling salesman problem）为例，这里简称TSP，TSP给出了不同的城市地点以及城市之间的距离，目的是为了找到最近的路线可以穿过所有的城市，并且每个城市只去一次

imageAddress: https://www.geeksforgeeks.org/wp-content/uploads/Euler12.png

Traveling salesman problem 与 Hamiltonian path 的区别：
Hamiltonian path 是一个cycle（圆形），现在又被称为 Hamilton's puzzle，是找到是否有一个环是可以实现每个地点走一次，但是 TSP 的目的是找出是否有一个最短的环

0x03 蚁群算法

蚁群算法（Ant Colony Optimization），在很多资料中也被称为蚁群优化算法，是一种基于种群的元启发式算法，可用于找到困难优化问题的近似解

蚁群中的蚂蚁可以通过某种信息机制进行信息传递，这种信息机制称为“信息素”

Photo by Maksim Shutov on Unsplash

信息素，也称做外激素，指的是由一个个体分泌到体外，被同物种的其他个体通过嗅觉器官（如副嗅球、犁鼻器）察觉，使后者表现出某种行为，情绪，心理或生理机制改变的物质。它具有通讯功能。几乎所有的动物都证明有信息素的存在。1959年发表雌蚕蛾会分泌性信息素，是科学界首次证明了性信息素是存在的。

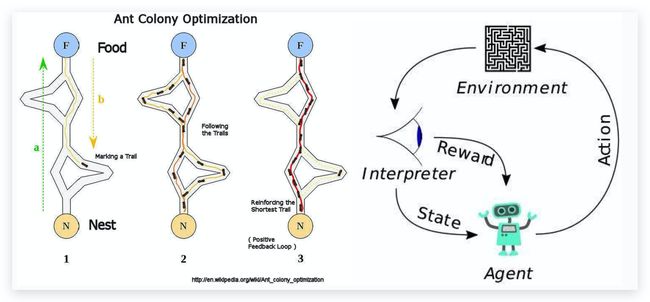
蚂蚁会在移动的过程中释放一种称之为“信息素”的物质，其他蚂蚁会对“信息素”具有感知能力，它们会沿着“信息素”浓度较高的路径行走，而每只路过的蚂蚁都会在路上留下“信息素”，这就形成了一种类似正反馈的机制，这样经过一段时间后，整个蚁群就会沿着最短路径到达食物源了

信息素值在运行时被修改，并表示蚁群的累积经验，而启发式值则是问题相关值，在TSP的情况下，启发式值被设置为边缘长度的倒数

蚁群效应认知步骤

1. 这些蚂蚁在开始前随意选择地点
2. 在每个构造步骤中，它沿着图的边缘移动
3. 每个蚂蚁都能记住自己的运行轨迹，在接下来的移动中，它会选择那些不通向它已经访问过的顶点的边
4. 蚂蚁一旦访问了图的所有顶点，就构造了一个解，在每一个构建步骤中，蚂蚁会在那些通向尚未访问的顶点的边缘中概率地选择要跟随的边
5. 概率规则受到信息素值和启发式信息的影响，信息素值和启发式值越高，蚂蚁选择这条边的概率就越高
6. 一旦所有的蚂蚁完成了它们的旅行，边缘上的信息素就会更新
7. 每一种信息素值最初都以一定的百分比下降
8. 随后，每条边接收到的额外信息素数量与它所属的解决方案的质量成正比

总结一下就是：
路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多

0x04 蚁群算法规则

1. 感知范围
   蚂蚁观察到的范围是一个方格世界，相关参数为速度半径，一般为3，可观察和移动的范围为3x3方格
2. 环境信息
   蚂蚁所在环境中有障碍物、其他蚂蚁、信息素，其中信息素包括食物信息素、窝信息素，信息素以一定速率消失
3. 觅食规则
   蚂蚁在感知范围内寻找食物，如果感知到就会过去；否则朝信息素多的地方走，每只蚂蚁会以小概率犯错误，并非都往信息素最多的方向移动。蚂蚁找窝的规则类似，仅对窝信息素有反应
4. 移动规则
   蚂蚁朝信息素最多的方向移动，当周围没有信息素指引时，会按照原来运动方向惯性移动，而且会记住最近走过的点，防止原地转圈
5. 避障规则
   当蚂蚁待移动方向有障碍物时，将随机选择其他方向，当有信息素指引时，将按照觅食规则移动
6. 散发信息素规则
   在刚找到食物或者窝时，蚂蚁散发的信息素最多，当随着走远时，散发的信息素将逐渐减少

0x05 蚁群算法特点

与其他优化算法相比，蚁群算法具有以下几个特点：

1. 采用正反馈机制，搜索过程不断收敛，最终逼近最优解
2. 每个个体可以通过释放信息素来改变周围的环境，且每个个体能够感知周围环境的实时变化，个体间通过环境进行间接地通讯
3. 搜索过程采用分布式计算方式，多个个体同时进行并行计算，大大提高了算法的计算能力和运行效率
4. 启发式的概率搜索方式不容易陷入局部最优，易于寻找到全局最优解

0x04 组合优化问题的形式化定义

将蚁群算法应用于组合优化问题(COP)的第一步是将COP模型定义为三元组(S，Ω，ƒ)，其中:

• S：在有限的离散决策变量集上定义的搜索空间
• Ω：变量之间的约束的集合
• ƒ：

  

  
  是一个需要最小化的目标函数

搜索空间S的定义如下:
一组离散变量 Xi(1,...,n)

S的元素是完整的赋值，即每个变量Xi都有一个从Di域中赋值的vji值
可行解集 SΩ 由 S 中满足集合Ω中所有约束条件的元素给出

解 s ∈ SΩ ，当下面的式子成立时，s为最优解

所有全局最优解的集合表示为

解决COP问题至少需要找到一个

（COP就是组合优化问题）

0x05 蚁群优化元启发式算法

在蚁群算法中，人工蚂蚁通过遍历全连通构造图来求解组合优化问题，定义如下:

1. 首先，每个实例化的决策变量 Xi=vji 被称为一个解决方案组件，并由cij表示
2. 所有可能的解决方案组件的集合用 C 表示
3. 构造图 GC(V,E) 通过将组件 C 与顶点 V 集或边 E 集关联来定义

信息素trail值 τij 与各组分 cij 相关。
(注意，信息素值通常是算法迭代t的函数，τij=τij(t))

信息素值允许对解决方案的不同组分的概率分布进行建模，蚁群算法在搜索过程中使用并更新信息素值

蚁群超启发式

Set parameters, initialize pheromone trails
SCHEDULE_ACTIVITIES
  ConstructAntSolutions
  DaemonActions    {optional}
  UpdatePheromones
END_SCHEDULE_ACTIVITIES

最著名的规则是蚂蚁系统(AS)的规则(Dorigo et al. 1991, 1996):

守护进程的行为

一旦建立了解决方案，在更新信息素值之前，通常可能需要一些问题的具体行动，这些操作通常被称为守护进程操作
可以用于实现特定于问题的和/或集中的操作，这些操作不能由单个蚂蚁执行

最常用的守护进程操作包括对构造的解决方案进行局部搜索，然后使用局部优化的解决方案来决定要更新哪些信息素值

更新信息素

信息素更新的目的是增加与好的解决方案相关的信息素值，并减少与坏的解决方案相关的信息素值
这是通过(i)通过信息素蒸发来降低所有信息素值，和(ii)通过选择一组好的解决方案来增加信息素水平Supd:

Supd：用于更新信息素的解集
ρ∈(0,1]：蒸发速率

信息素的蒸发实现了一种有用的遗忘形式，有利于探索搜索空间中的新领域
不同的蚁群算法，例如蚁群系统(ACS) (Dorigo & Gambardella 1997)或MAX-MIN蚂蚁系统(MMAS) (Stützle & Hoos 2000)，更新信息素的方式不同。

0x06 主要ACO算法

这里概述了三个最成功的系统：

• 蚂蚁系统 Ant system
  (Dorigo 1992, Dorigo et al. 1991, 1996)
• 蚁群系统 Colony system
  (ACS) (Dorigo & Gambardella 1997)
• MAX-MIN蚂蚁系统 MAX-MIN ant system
  (MMAS) (Stützle & Hoos 2000)

为了清楚地说明它们之间的区别，使用旅行推销员问题的例子

Ant system

蚁群算法(Ant system, AS)是文献中提出的第一个蚁群算法(Dorigo et al. 1991, Dorigo 1992, Dorigo et al. 1996)
特点：所有完成的蚂蚁都会更新信息素值

求解分量cij为图的边，τij的信息素更新，即连接边城市i和j的信息素更新如下:

ρ∈(0,1]：蒸发速率
m：蚂蚁的数量

：第k只蚂蚁在边缘放置的信息素的数量

Lk：第k只蚂蚁的旅行长度

蚁群在构造解时，遍历构造图，并在每个顶点进行概率决策

第k只蚂蚁从城市i到城市j的转移速率

Ant colony system

最初提出的蚂蚁系统的第一个重大改进是Dorigo和Gambardella(1997)引入的蚁群系统(ACS)
ACS和AS之间的第一个重要区别是蚂蚁在构建过程中使用的决策规则的形式

ACS中的蚂蚁使用所谓的伪随机比例规则：蚂蚁从城市i移动到城市j的概率取决于一个均匀分布在[0,1]上的随机变量q和一个参数q0
当q≤q0时，在可行分量中，选择使

乘乘积最大化的分量，否则，使用与as中相同的方程

这一贪心的规则有利于信息素信息的利用，通过引入一个多样化的组件：局部信息素更新来抵消这一规则
每一步构建完成后，所有蚂蚁都进行局部信息素更新。每只蚂蚁只将它应用于最后一条经过的边

ρ∈(0,1]：信息素衰变系数
τ0：信息素的初始值

本地更新的主要目标是使后续蚂蚁在一次迭代中执行的搜索多样化
在一次迭代中，降低边缘上的信息素浓度会鼓励随后的蚂蚁选择其他边缘，从而产生不同的解决方案
这使得在一次迭代中，几只蚂蚁不太可能产生相同的解决方案，由于ACS中信息素的局部更新，使得信息素的最小值受到限制

与As一样，ACS也在构建过程的最后执行信息素更新，称为离线信息素更新

根据公式，ACS离线信息素更新仅由最优蚂蚁执行，即仅更新被最优蚂蚁访问过的边

ACS引入的大部分创新都是在Ant-Q中首先引入的，Ant-Q是ACS的一个初步版本，由同一作者提出

MAX-MIN ant system

MAX-MIN蚂蚁系统(MMAS)是由Stützle和Hoos(2000)提出的对原始蚂蚁系统思想的另一种改进
MMAS与AS的不同之处在于：

1. 只有最好的蚂蚁信息素轨迹补充道
2. 最小值和最大值的信息素是显式有限(在ACS这些值是有限的隐式,即限制的值是一个结果的算法工作而不是一套价值明确的算法设计)。

信息素更新方程的形式如下:

当最优的蚂蚁使用边(i,j)时，

：最优蚂蚁的路线长度
在ACS中，Lbest可以(根据算法设计者的决定)设置为Lib或Lbs，或两者的组合il;

References
https://www.jianshu.com/p/6d16573ef675
http://www.scholarpedia.org/article/Ant_colony_optimization