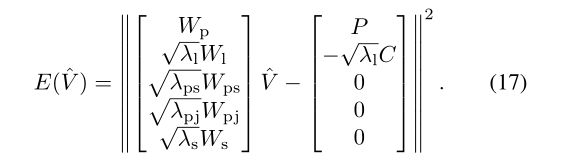【论文精读】Single-Perspective Warps in Natural Image Stitching-自然图像拼接中的单透视扭曲

论文下载链接
两张图像拼接代码链接
多张图像拼接代码链接

这篇论文Single-Perspective Warps in Natural Image Stitching 是Tianli Liao和Nan Li在2018年发表的关于单透视扭曲图像拼接的论文。

摘要

首先介绍了图像拼接在视觉上的分类：①单透视；②多透视。单透视结果在透视一致性方面优于多透视结果，但存在投影失真。
本文提出了两种用于自然图像拼接的单透视扭曲。①参数扭曲：通过双重特征将尽可能多的投影扭曲和准单应性扭曲结合起来。②基于网格的扭曲：通过优化总能量函数来确定，该函数同时强调单个透视扭曲的不同特征，包括对齐、自然度、扭曲和显著性。

一、介绍

1、介绍了几种常用的扭曲形式：
①全局翘曲[2]-[4]：通过一个统一的全局变换(主要是单应性)来最小化重叠像素之间的对准误差，具有鲁棒性，但不够灵活。
②空间变化的翘曲[5]-[7]：采用多个局部变换(位置相关)来提高对准精度。
③接缝驱动翘曲[8]-[10]：不是采用全局最小化来对齐误差，而是寻找局部重叠像素进行无缝拼接。

总结：上述的几种翘曲大多使用单应性正则化将翘曲平滑外推到非重叠区域，拼接结果本质上是单视角的，因此在单应性翘曲时存在投影畸变，即形状/面积严重拉伸和非均匀放大。

2、图像拼接中的失真问题如何解决？
[11]–[13]采用了在重叠区域具有更好对齐的扭曲和在非重叠区域具有较少失真（主要是相似性）的扭曲的组合来解决失真问题。需要注意，在[13]中，它使用准单应性扭曲作为扭曲较少的扭曲。

3、针对整体拼接结果的自然性问题，[14]提出了一种方法，即引导经纱进行全局相似经纱，以最小线畸变旋转或[15]避免提取的线段弯曲。由于人眼对线条更为敏感，[16]强调双特征(点+线)有助于提高图像扭曲的自然质量。

二、相关工作

A、扭曲为了更好的对齐

传统方法使用全局扭曲（如相似性、仿射和单应性）来对齐重叠区域中的图像[3]，很稳健，但不够灵活，无法精确对齐。Gao等人[5]提出了一种双单应（DH）扭曲方法，通过两个单应的加权和来处理具有两个主平面的场景。Lin等人[6]提出了一种平滑变化仿射（SVA）扭曲，它用平滑仿射缝合场代替全局仿射扭曲。Zaragoza等人[7]在移动DLT框架中提出了一种尽可能投影的（APAP）扭曲，它能够微调全局单应性扭曲，以适应位置相关对齐。[17]–[19]将图像对齐与接缝切割相结合，以找到可以无缝混合的局部对齐区域，而不是全局对齐整个重叠区域。Gao等人[8]提出了一种接缝驱动的方法，该方法以最小的接缝成本而不是最小的对齐误差找到单应性扭曲。Zhang和Liu[9]提出了一种视差容忍扭曲，它将单应和内容保持扭曲结合起来，以局部对齐图像。Lin等人[10]提出了一种接缝引导的局部对齐方法，该方法通过根据到当前接缝的距离自适应特征加权来迭代改进扭曲。

B、减少变形的扭曲

许多努力都致力于减轻非重叠区域的扭曲。一项开创性的工作[4]使用球形或圆柱形翘曲产生多透视结果来解决这个问题，但它必须弯曲直线。Chang等人[11]提出了一种保形半投影（SPHP）扭曲，该扭曲在空间上结合了单应性扭曲和相似性扭曲，从而在重叠区域保持良好对齐，同时在非重叠区域保持原始透视。Lin和Pankanti[12]提出了一种尽可能自然的自适应（AANAP）扭曲，该扭曲将线性化单应性扭曲和具有最小旋转角度的全局相似性扭曲相结合，从而使缝合结果看起来更自然。Li等人[13]提出了一种准单应性（QH）扭曲，以平衡非重叠区域中的透视失真和投影失真，从而产生单一透视拼接结果。

C、扭曲以获得更好的自然度

近年来，一些拼接方法通过能量最小化来实现网格变形来模拟图像扭曲。通过强调线条特征来解决自然性问题。Chen等人[14]提出了一种全局相似性（GSP）扭曲，该扭曲约束扭曲以最小的线失真旋转进行全局相似性扭曲。Zhang等人[15]提出了一种扭曲来生成宽基线场景的正交投影，该投影约束扭曲以保留提取的线段。Li等人[16]提出了一种基于双特征（DF）的扭曲，它不仅提高了低纹理情况下的对齐精度，还防止了一些不必要的失真。

三、单透视参数扭曲

单应性扭曲是用于图像缝合的最经典的单透视扭曲，但它带有运动假设，即图像是通过纯旋转摄影机运动拍摄的，或场景假设，即场景的几何体是平面的或实际上是平面的，例如场景距离足够远。如果不满足这些条件，换句话说，摄影机运动涉及平移，场景涉及非平面几何体，则单应变形不可避免地会在全景中引入对齐、失真和自然性问题。事实上，在运动和场景的一般假设下，单应变形通过“最小二乘”意义上的共同主平面将来自不同视图的同一场景的图像关联起来。在本节中，我们首先从对齐、变形和自然度方面对单透视扭曲进行分析，然后提出一个参数扭曲来解决这三个问题。

A、数学设置

设I和I’分别表示目标图像和参考图像。单应曲H是一种平面变换，它将像素坐标(x, y)∈I与(x '， y ')∈I '联系起来

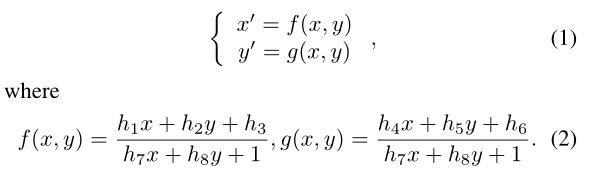
B、对齐问题

通常，通过直接线性变换（DLT）从一组特征对应关系估计H。假设给定的特征对应来自场景的平面几何体，则H是不同视图中它们之间的精确单应性。如果它们来自非平面几何体，则H是通过公共主平面将I与I’联系起来的近似单应性，该平面符合“最小二乘”意义上的给定特征对应关系。直观地说，对齐质量对于离平面更近的内容更精确，而对于离平面更近的内容更差（见图2（a））。

与使用单个全局单应性扭曲来对齐图像不同，APAP[7]使用空间变化的扭曲H∗ 它由多个局部单应性扭曲组成，用于图像对齐。换句话说，APAP不是使用公共主平面来近似场景的非平面几何体，而是使用重叠区域中的空间变化平面场，该场演变为非重叠区域中的公共主平面。这种方法被称为移动DLT，已被证明对图像对齐非常有效，特别是在一般运动和非平面场景的情况下。值得注意的是，APAP仍然创建一个透视拼接结果（参见图2（b））。

C、自然性问题

假设场景的几何体实际上是平面的，那么H将创建一个自然的全景。对于基本的两幅图像拼接问题，这意味着H将I的透视图转换为I’，从而使I在不违反任何相对几何的情况下扭曲为I’的扩展视图。如果场景的几何体是非平面的，那么由H创建的全景可能看起来不太自然，这可以从直线方向明显观察到（见图2（a））。H∗也可能会遇到自然性问题，因为重叠区域中的线的不可见错位会放大为整体缝合结果中的相对几何图形的可见违规（见图2（b））。
实际上，在特征对应中考虑双特征[16]有助于提高自然质量。与仅通过点特征估计翘曲相比，通过DF的H[16] (或H∗[20])不仅强调重叠区域的对齐质量，而且还强调整体拼接结果的自然质量(见图2(d,e))。换句话说，共同的优势面更能保护在重叠区域内的线不偏离。

D、失真问题

除了对齐和自然性问题外，H和H∗ 在非重叠区域中可能仍然存在失真问题。直观地说，对于靠近公共主平面的内容，失真可以忽略不计，但是对于离开平面的内容，失真会变得更严重（见图2（a、b、d、e））。
与使用单应正规化H和H∗相比，QH[13]使用准单应正规化H†，可以缓解失真并保留透视。回想一下，H†可以表述为一个二元系统的解

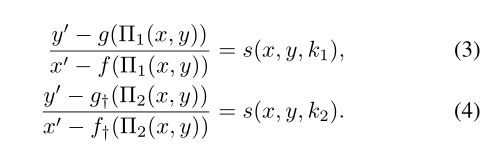
图3(b)显示了QH的草图，其中点Π1(x, y)和Π2(x, y)(红色和蓝色)是(x, y)(黄色)在相交于(x∗，y∗)(红色和蓝色)的十字线lu和lv(红色和蓝色)上的投影。此外，k1·k2=−1,f†(x, y)， g†(x, y)是f, g(2)在(x∗，y∗)的泰勒级数的一阶截断，s(x, y, k)是通过(x, y)的线的斜率，其斜率为

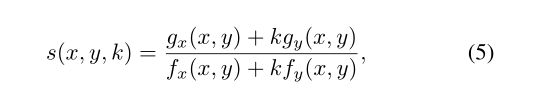
其中fx，fy，gx，gy表示f，g的偏导数。
在[13]中，通过假设定向相机通过水平运动拍摄图像，lu被设置为扭曲后保持水平的水平线，lv被设置为最接近重叠区域和非重叠区域边界的垂直分割线。事实上，如果给定单应性扭曲，则存在唯一的平行线族，该平行线族在扭曲后仍保持平行。它们的斜率可以通过求解sx=sy=0来确定，其中sx，sy表示s（x，y，k）的偏导数。翘曲前后平行板的坡度为

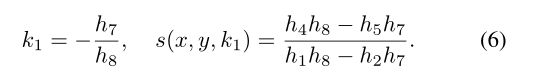
因此，可设lv为斜率k1最接近交叠区域与非交叠区域边界的分割线，而lu可设为翘曲前后与lv正交的线，即

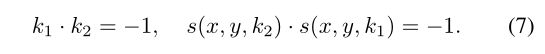
事实上，（6,7）有助于QH摆脱相机方向和运动的假设。此外，平行于lv的平行线族上的长度比保持不变。换句话说，H†沿每条线的方向导数与斜率k1为常数，这与[11]中的坐标变化技术一致。我们使用分析来描述单透视网格变形的变形问题（见第IV-D节）。

E、组合扭曲

用APAP 扭曲 H∗组成QH 扭曲 H†

创建一个看起来更自然的单透视结果(参见图2(c,f))，其中H是单应弯曲，从H∗推断到H†。

四、单透视网格变形

APAP、DF和QH的组合通常会产生一种自然的单透视缝合效果，但翘曲仍然会弯曲一些突出的线条（见图6（a））。为了解决这一问题，我们提出了一种基于网格的扭曲，该扭曲将对齐、自然度、失真和显著性问题视为不同的能量项，然后最小化总能量函数以获得所需的单透视扭曲。

A、数学设置

让I和I’分别表示目标图像和参考图像。在为I构建网格并将网格顶点从1到n进行索引后，我们将n个顶点重塑为2n维向量V=[x1y1x2y2…xnyn]T，然后网格变形后相应的向量形成V’=[x1’y1’x2’y2’…xn’yn’]T。
与[21]类似，对于I中的任意采样点p，我们将其描述为其四个外围网格顶点v1, v2, v3, v4的双线性插值，即，

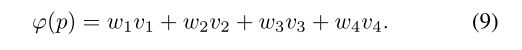
通过假设系数是固定的，则对应点p’的特征为双线性插值φ（p’）=w1v1’w2v2’w3v3’w4v4（见图4）。因此，点对应的任何约束都可以表示为顶点对应的约束。
经过上述准备，我们定义了总能量函数

其中Ep(V’)通过加强点对应来解决对齐问题，E1(V’)通过加强线对应来解决自然问题，Ecl(V’)通过单应性弯曲先验重新排列交叉线对应来解决畸变问题，Es(V’)通过保护显著线不被弯曲来解决显著性问题。通过求解最小E(V’)来确定基于网格的经度。

B、对齐项

给定点对应集{（pi，pi’）}Ni=1，其中pi=（xi，yi）∈I和p’I=（xi’，yi’）∈I’（见图5（a）），然后

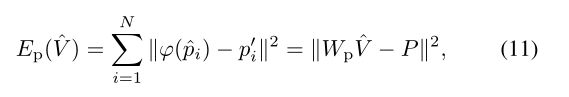
其中P∈R2N由pi’，Wp的坐标组成∈R2N×2n由pi′的双线性插值坐标的系数向量组成。

C、自然项

已知直线对应集{(lj, lj’)}Mj=1，其中lj∈I由起始点psj，终点点pej的线段表示，lj’∈I’由直线方程ajx+bjy+cj= 0表示(图5(a))

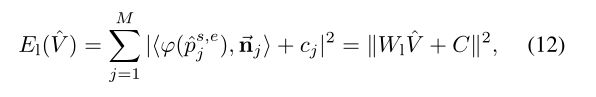
其中nj’=（aj，bj）T，C=（c1，c1，…，cM，cM）T和Wl∈ R2M×2n由ps’，ej和nj’的双线性插值内积的系数向量组成。

D、畸变项

受上述准单应性扭曲的启发，我们将Ecl（V’）划分为Eps（V’），Eps（V’）保留单应性扭曲之前和Epj（V’）给出的期望透视图。该准单应性扭曲通过线性化lu上的比例来缓解失真，同时通过保持平行于lu和lv的交叉线的相应斜率来保持透视图这减轻了投影失真。
给定交叉线对应集{（lui，l’u i）}Si=1和{（lvj，l’v j）}Tj=1，其中lui和lvj平行于从单应性扭曲先验计算的lu和lv，然后我们用Li和Kj点{pu，ik}Lik=1和{pv，jk}Kj k=1（见图5（b）），然后对它们进行均匀采样

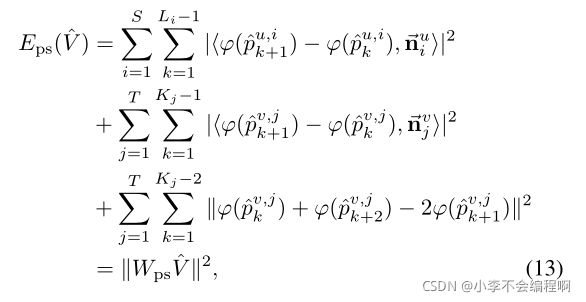
其中nui’和nvj’是l’u i和l’vj的法向量，Wps∈R(PS i=1(Li−1)+PT j=1(3Kj−5))×2n。实际上，前两项保留了l’ui和l’vj的斜率，最后一项保留了lvj的长度比。
让Ω 表示I的非重叠区域的前像，然后

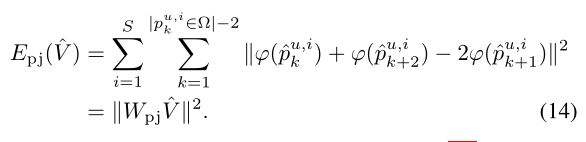
其中Wpj∈R ΣS i=12(|pu,i k∈Ω|−2)×2n。事实上，(14)在Ω中线性化了lui的尺度。

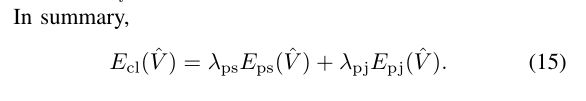
E、显著项

给定显著线集合{lsk}Qk=1，其中每个lsk∈I均采用Jk点{pkj}Jkj=1均匀采样(图5©)，则

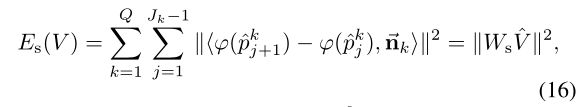
其中，nk '是l ’ sk∈I '的法向量，由单应性弯曲先验计算而w∈R ΣQ k=1(Jk−1)×2n。
图6显示了具有不同λs值的比较示例，这表明了显著性项保护显著线的能力。

F、优化

因为所有项都是二次项，所以我们将总能量函数（10）改为

任何稀疏线性解算器都可以有效地求解最小E（V’）。

五、实现

A、两幅图拼接

给定一对两幅图像，我们首先使用将目标透视变换为参考透视的点和线对应来估计单应性扭曲，然后在目标图像中均匀采样计算出的交叉线对应和检测到的线段，最后，我们优化总能量函数以获得扭曲的结果。算法1给出了一个简单的算法。

B、多幅图拼接

给定一系列多幅图像，我们的拼接策略包括三个阶段。在第一阶段中，我们选择一个参考图像作为标准透视图，以便其他图像与它保持一致。然后，我们估计每个图像的单应变形，并通过束调整在参考坐标系中进行变换。我们的束调整方法与[22]不同，因为我们将线对应作为点对应的补充，因此结果看起来更自然（见图7）。最后，我们通过同时优化一个能量函数来获得每个图像的扭曲结果。

1）束调整：

对于一组输入图像{Ik}Kk=1，我们首先选择一个参考帧I '。为简单起见，I '是从{Ik}Kk=1中的一个中选择的。然后通过单应性链将所有点和线的特征映射到I '上。在I '坐标系中，只对线特征的两个端点进行映射，并对具有相同恒等式的坐标(点和线)进行平均。这个过程得到一个集合坐标{pi '}Ni=1的点对应和一个集合坐标{qs '，ej}Mj=1的线对应。最后，我们同时最小化所有点和线对应的传递误差。具体来说，我们最小化能量函数

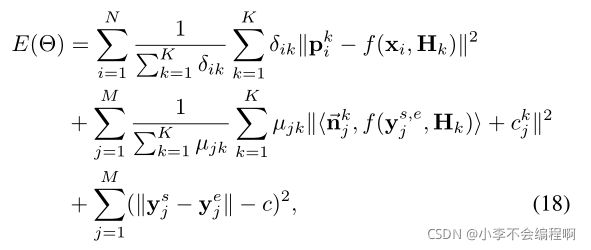
2）同时优化：

通过束平差确定单应{Hk}Kk=1后，我们可以用H−1 k将每个目标图像Ik的视角转换为参考图像I '的视角，并用H−1 k来计算跨线对应集。

六、实验

我们从两个方面证明了基于网格的扭曲的有效性。首先，我们对我们的翘曲与两种最先进的单视角翘曲(单应性和APAP[7])的对准精度进行了定量评估。其次，通过与单应性、APAP、AutoStitch[4]、SPHP[11]和GSP[14]这五种最先进的扭曲进行比较，对自然质量进行了定性评价。我们还比较了基于网格的扭曲与单应、APAP、SPHP、GSP和QH[13]的时间效率。
在实验中，我们使用VLFeat[24]提取并匹配SIFT[25]特征，使用RANSAC[26]去除异常值，使用LSD[27]检测线段并通过[28]进行匹配。在参数设置上，网格变形将网格尺寸设置为40×40，能量最小化将λl、λps、λpj设置为5、50、5，在实验中相对稳定。值得注意的是，显著项和投影项是竞争性的。这意味着，如果λs太小，则显著线明显弯曲；如果λs太大，则投影失真变得严重。在实验中，我们发现λs=5是一个合适的折中方案（见图6（b-d））。
代码在MATLAB中实现(为了提高效率，有些是用c++实现的)，实验是在Intel i5 2.9GHz CPU和8GB RAM的台式机上进行的。

A、对齐的定量评价

我们定量评估了我们提出的基于网格的翘曲的对准精度，该精度由一组点对应{pi，pi’}Ni=1上的均方根误差（RMSE）测量，

与APAP类似，我们将可用的SIFT特征对应随机划分为大小相同的“训练”和“测试”集。训练集用于学习翘曲，RMSE在两个训练集上进行评估。我们将我们的扭曲与单应（Homo）和APAP（使用作者提供的实现）进行比较。
我们还采用了[29]中的像素误差度量，其中I中的像素x被标记为离群值，如果在I '中的t(x)的4像素邻域内没有相似的像素(强度差小于10个灰度级)。然后将t在重叠区域产生的离群值的百分比作为翘曲误差。我们评估三个不带或带双重特征的扭曲的%异常值，这些异常值显示在“/”之前和之后。

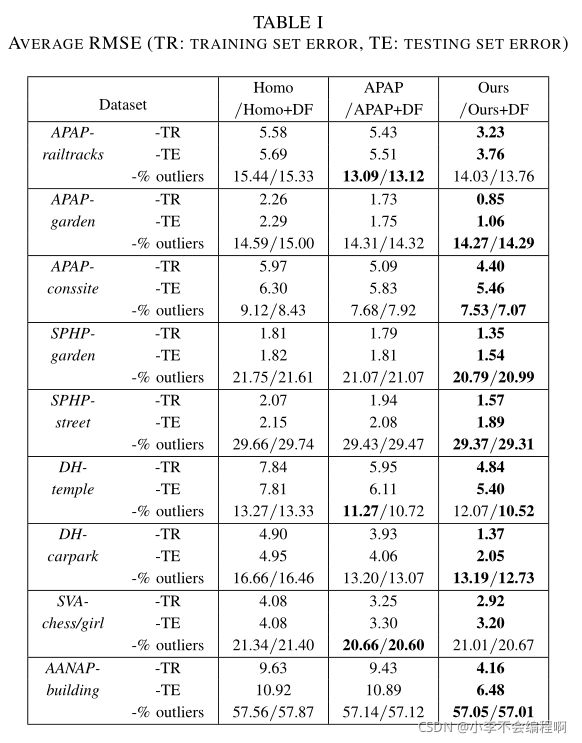
表一显示了来自APAP、SPHP、DH、SVA和AANAP的九个挑战性图像对20次重复的平均RMSE和%异常值。很明显，对于大多数对，我们的扭曲产生的误差最小（粗体值）。

B、自然性的定性评价

我们定性地比较了我们提出的基于网格的扭曲与单应、APAP、AutoStitch、SPHP和GSP的自然质量。图8和图9展示了四个比较结果，其中输入图像来自一些开放数据集。很明显，我们的扭曲在自然度、扭曲度和显著性方面创造了更自然的缝合效果。补充资料中提供了我们的数据集和其他数据集（包括DH、CAVE[30]、SPHP、AANAP、GSP和APAP）的更多总体性能比较结果。

C、时间效率

我们将我们提出的基于网格的扭曲与一些公开的扭曲、单应、APAP、SPHP、GSP和QH进行了时间效率比较。所有基于网格的方法都以相同的网格大小运行。
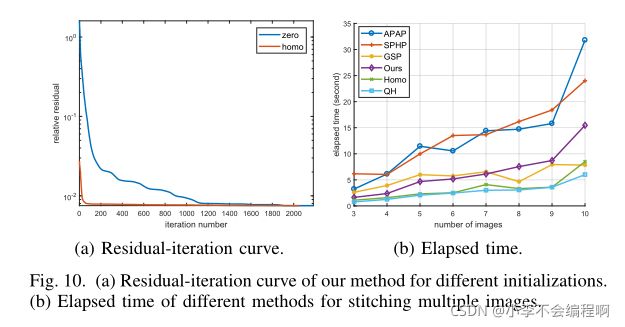
图10（a）显示了不同初始化的扭曲的剩余迭代曲线。对于单应的初始化，收敛速度要快得多。
图10(b)显示了不同的多幅图像拼接方法的耗时。除了GSP在c++中运行，其他的方法都在MATLAB中运行。记录的时间包括网格优化、纹理映射和线性混合，其中不考虑特征检测和匹配。很明显，单应性和QH是最有效的弯曲。APAP是效率最低的翘曲，因为它计算了许多局部单应翘曲。GSP和我们的扭曲是比较的，因为它们都是同时解决网格变形。

D、错误案例

如果重叠区域的视差过大，我们提出的扭曲可能会失败，这样公共主平面就不能很好地表示图像之间的透视变换。

七、总结

在本文中，我们提出了两种用于图像拼接的单透视扭曲，以使拼接结果看起来尽可能自然。第一个是参数化扭曲，它是APAP和QH通过DF的组合。第二种是基于网格的扭曲，通过优化稀疏和二次总能量函数来确定。综合评估表明，所提出的扭曲优于一些最先进的扭曲，包括单应、APAP、AutoStitch、SPHP和GSP。

完！