大数据基础与应用课程作业一：数据预处理

---

数据预处理作业题目

作业用到的数据集：
链接: churn数据集
提取码：6666
这个数据集应该是记录用户特征与是否流失的数据集，今天使用churn数据集对数据进行预处理。

---

一、总览

数据库中包含的大部分原始数据都是未经预处理、不完整且存在大量噪声的。
存在过时、冗余的字段
存在缺失值
存在异常值
数据格式不适合进行数据挖掘
数据不符合政策或者常识
因此，在进行数据挖掘之前需要进行数据清洗。
实际上，在实际操作中，数据清洗通常会占据分析过程的50%—80%的时间

二、R和Rstudio一些操作

1.R注释

R只支持单行注释，注释符号为 #

2.工作路径的设置

要打开数据集文件，可以使用绝对路径，但用过python编辑器，如pycharm或jupyter notebook就会明白，可以使用相对路径，但是使用相对路径就需要对当前工作路径搞清楚。
在Rstudio中，修改工作路径的文章already exists，please refer to the link:
Rstudio中修改工作路径的三种方法
下面展示my operation:

getwd() # output:"C:/Users/Jiacheng/Documents"

我在D盘下新建了一个文件夹用于存放数据集和代码，因此选择的是第二种global options设置

3.清除历史记录、变量等

参阅：RStudio 清除历史记录，变量，窗口
abstract:
清空控制台:

Ctrl+L

清除变量历史记录

rm(list = ls())

三、预处理工作

1.查看数据是否具有缺失值

(1)实验代码

churn=read.csv("datasets/churn.txt",stringsAsFactors=TRUE)
any(is.na(churn))

(2)原理介绍

read.csv(“datasets/churn.txt”,stringsAsFactors=TRUE)
   以CSV格式读取数据集文件，stringsAsFactors参数表示将字符串转化为factor,参见解释
is.na(churn)
   返回和churn维度相同的dataframe，里面的值为布尔值，标志churn对应位置是否是空值
any(x)
   判断表达式是否至少有一个为TRUE

(3)实验结果

(4)结果解释

出现了这个结果，说明churn里面每一个element都不是空值

2.检查state和Area.code字段的异常

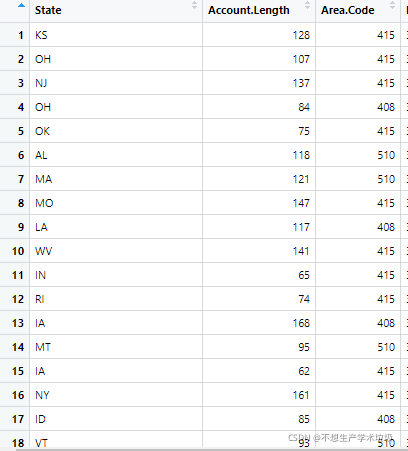
美国各州的行政区简称参阅：百度百科
美国各州的地区码对应关系参阅：美国各州区号查询
美国各州与其地区码是一对多的关系，一个州可以有多个地区码，而一个地区码只能对应一个州。
参阅链接2，可知地区码415是加利福尼亚州的一个区号，而在数据中415却对应了堪萨斯州、俄亥俄州等，这里是明显的abnormal.

3.可视化检查CustServ.Calls的离群点

(1)实验代码

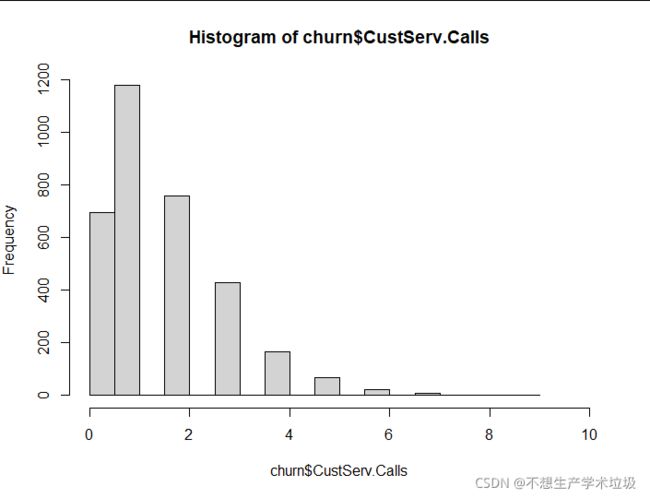
hist(churn$CustServ.Calls,xlim = c(0,10))

(2)原理介绍

hist(churn$CustServ.Calls)
   churn$CustServ.Calls表示将churn中的CustServ.Calls字段取出
   hist函数用于绘制直方图，其中可以设置绘制范围、直方图cell的大小等

(3)实验结果

(4)结果解释

根据直方图可以看出，the number of calls to customer service在5、6、7、8、9次时，是离群点

4.使用z-score、IQR方法判断CustServ.Calls离群点

(1)实验代码

churn$z_custcall=(churn$CustServ.Calls-mean(churn$CustServ.Calls))/sd(churn$CustServ.Calls)
list = which(churn$z_custcall>3 | churn$z_custcall< -3)
unique(churn[list,]$CustServ.Calls)

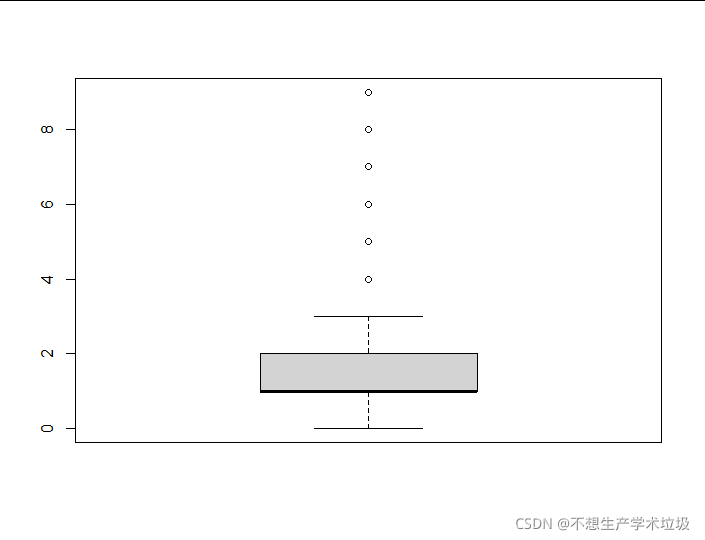
boxplot(churn$CustServ.Calls)    #  绘制箱线图

(2)原理介绍

boxplot()函数用于绘制箱线图
which()函数返回满足条件表达式的行的行号
unique()函数返回切片后取CustServ.Calls列中不重复出现的特征值

z-score的公式如下图：

在z-score标准化后，可以假定数据服从标准正态分布，根据3-σ准则，可以认为大于3或者小于-3的值是离群点。
箱线图的原理是数据的四分位数，如下图所示：
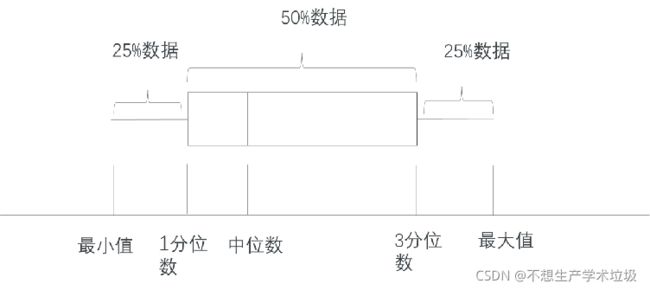在使用箱线图对离群点进行检测时，计算四分位数：Q1,Q2,Q3 分别是25%，50%，75%分位数，IQR=Q3-Q1，小于Q1的1.5* IQR或者大于Q3的1.5* IQR ，判断为离群点。

(3)实验结果

(a)z-score结果

(b)箱线图结果

(4)结果解释

z-score返回结果说明the number of calls to customer service在6、7、8、9次时是离群点。
由箱线图可知，the number of calls to customer service 在4、5、6、7、8、9次时是离群点。
根据两次结果和上一个题作比较，在上一题中得到的离群值5、6、7、8、9，其实是比较保守的主观估计，因为这里面没有引入定量的指标，完全依靠观测者的主观感受。在本题中z-score得到的离群点明显要少于上一题和箱线图的结果，这是因为离群点本身就会影响z-score中的均值的标准差，因此离群点的大小和数量是会对结果造成较大影响的。
因此，IQR方法判断离群点更加robust。

5.对day minutes属性进行z-score标准化

(1)实验代码

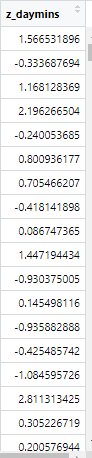
churn$z_daymins=(churn$Day.Mins-mean(churn$Day.Mins))/sd(churn$Day.Mins)

(2)原理介绍

z-score原理在上面介绍过，不再赘述。

(3)实验结果

(4)结果解释

无

6.计算倾斜度

(a)计算day minutes的倾斜度
(b)计算day minutes进行z-score后的倾斜度，与上一个计算作比较
(c)根据之前计算的倾斜度，是否能认定day minute这个属性是倾斜的或者是近乎完美对称的。

(1)实验代码

3*(mean(churn$Day.Mins)-median(churn$Day.Mins))/sd(churn$Day.Mins)
3*(mean(churn$z_daymins)-median(churn$z_daymins))/sd(churn$z_daymins)

(2)原理介绍

倾斜度的的定义为：

倾斜度大于0和小于0的两种情况如下图所示：

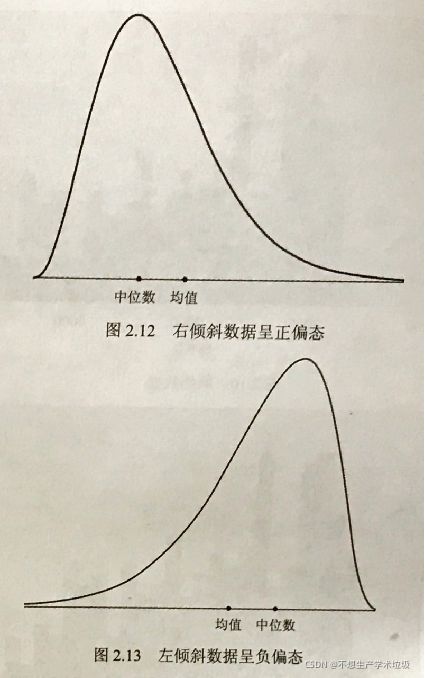
(3)实验结果

(4)结果解释

由结果可知在经过z-score前后，倾斜度的计算结果不变。由于倾斜度很小，仅为0.02左右，是可以认为它是完美对称的。

7.对day minutes属性构建正态概率图

(1)实验代码

qqnorm(churn$z_daymins,
       datax = TRUE,
       col = "red",
       #ylim = c(0.6931, 4.7875),
       #main = "对数变换后的dist的Q-Q图"
) #画QQ图
qqline(churn$z_daymins,
       col = "blue",
       datax = TRUE)#画对比直线

(2)原理介绍

QQ图是一种常见的用于衡量两个分布的相似性的方法，原理如下：

首先画出两个分布的CDF图，
如红色虚线所示，对于一个概率，得到这两个分布的分位数x0和y0，然后以(x0,y0)为坐标在QQ图中画一个点。
变化不同的概率，重复上述步骤，就可以得到不同的点，把这些点连接起来就是QQ图。
如果两个数据集的分布一致，画出的线是一条直线。

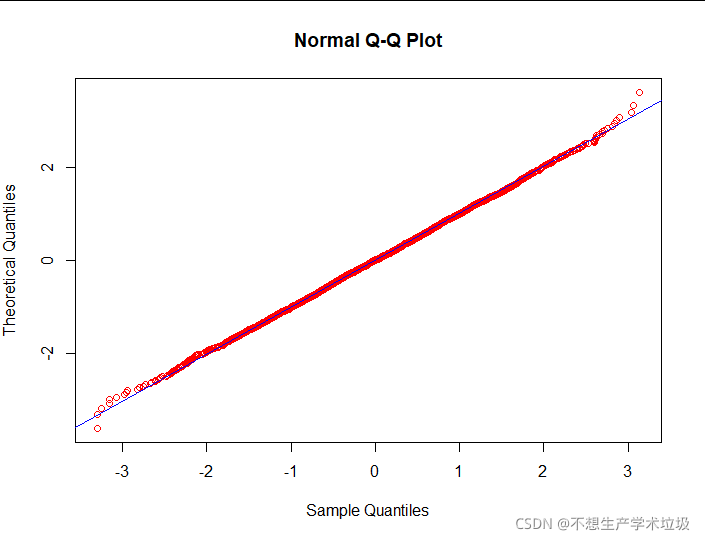
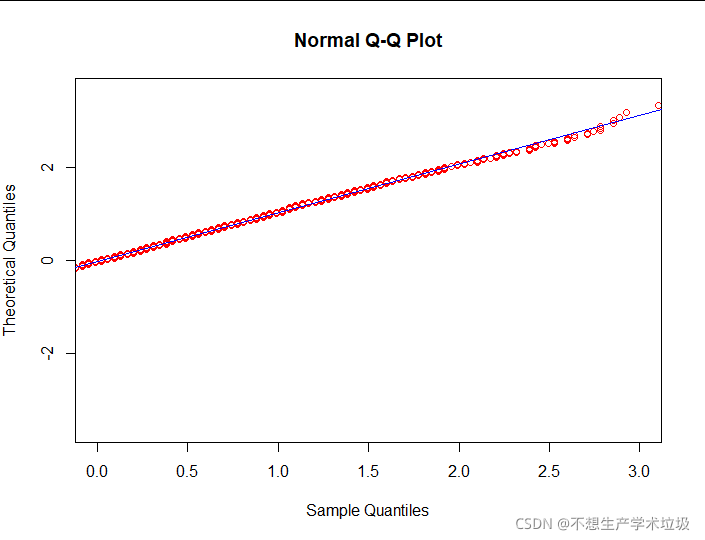
(3)实验结果

(4)结果解释

由上图可以看出，z-score后的day minutes的概率分布与标准正态分布的QQ图与一条直线很相像，故可以认为具有正态性。

8.对international minutes属性分析

(a)构建正态概率图
(b)是什么导致这个属性不服从正态分布的
(c)构建一个标志变量能够指示(b)中出现的这种情况
(d)对于非负的international minutes进行绘制正态概率图，判断其正态性

(1)实验代码

churn$z_IntlMins=(churn$Intl.Mins-mean(churn$Intl.Mins))/sd(churn$Intl.Mins)
# 进行z-score标准化
qqnorm(churn$z_daymins,
       datax = TRUE,
       col = "red",
       #ylim = c(0.6931, 4.7875),
       #main = "对数变换后的dist的Q-Q图"
) #画QQ图
qqline(churn$z_daymins,
       col = "blue",
       datax = TRUE)#画对比直线
# 以上是绘制全部的qq图
qqnorm(churn$z_daymins,
       datax = TRUE,
       col = "red",
       ylim = c(0, 3),
       #main = "对数变换后的dist的Q-Q图"
) #画QQ图
qqline(churn$z_daymins,
       col = "blue",
       datax = TRUE)#画对比直线
# 以上只对y>0的地方进行绘制

(2)原理介绍

无

(3)实验结果

对Intl.Minsz-score标准化后，绘制的QQ图如下图所示：

只对非负部分进行绘制：

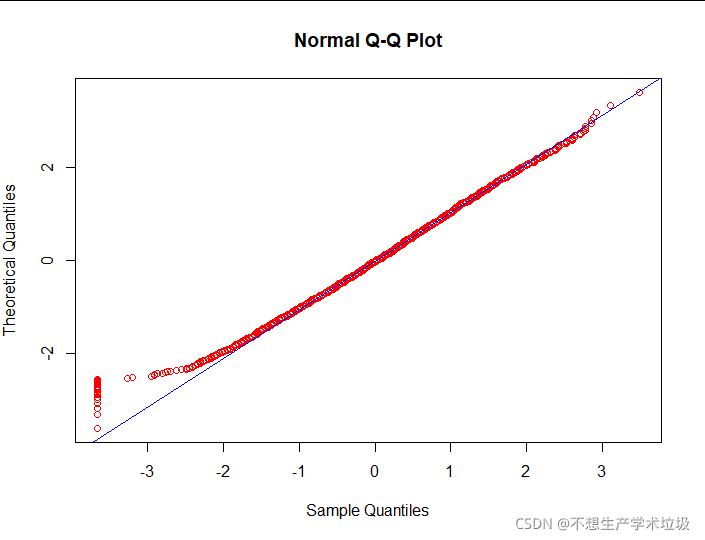
(4)结果解释

(b)可以从第一张图看出，在真实数据中有太多的离群点，造成这样的原因是有相当一部分人几乎不打国际电话。但是这种看似是“离群点”，其实它却对数据后面的部分符合正态分布做出了不小的贡献。
©可以用离群点占总点数的比例来看，根据比例来对离群点的严重情况进行处理。如可以利用3-σ准则，如果离群点的数量超过了3-σ准则所规定的，那么就要进行进一步的处理了。
(d)仅显示非负部分的QQ图可以看到数据与正态分布拟合得很好。

9.对night minutes进行z-score并用图describe标准化后得取值范围

(1)实验代码

churn$z_netmins=(churn$Night.Mins-mean(churn$Night.Mins))/sd(churn$Night.Mins)
boxplot(churn$z_netmins)

(2)原理介绍

无

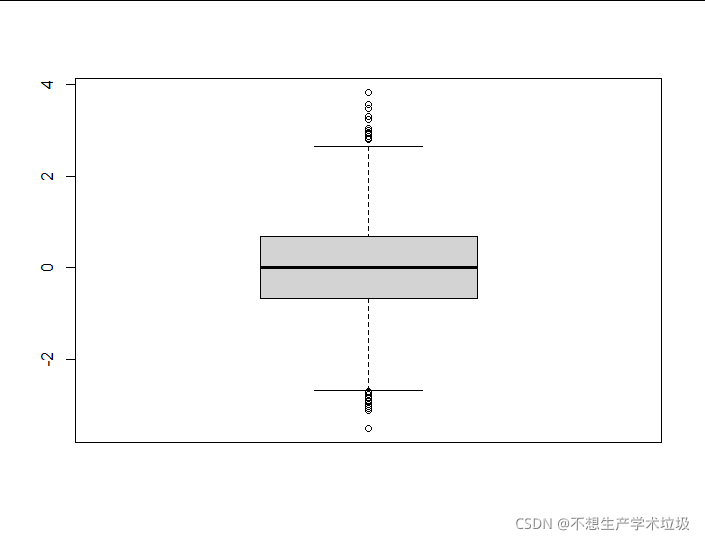
(3)实验结果

(4)结果解释

使用箱线图对标准化的值进行范围显示，按照箱线图的理论，在最上下两根线之间范围内的值为正常值，之外的都是离群值。

---