PCL 曲率计算

一、曲率

点云的曲率及计算_点云侠的博客-CSDN博客_点云曲率计算

曲率是曲线弯曲程度的一个度量。

曲率的分类：

1、主曲率、平均曲率、高斯曲率

主曲率：

主曲率计算源码：

//
template  void
pcl::PrincipalCurvaturesEstimation::computePointPrincipalCurvatures (
      const pcl::PointCloud &normals, int p_idx, const pcl::Indices &indices,
      float &pcx, float &pcy, float &pcz, float &pc1, float &pc2)
{
  EIGEN_ALIGN16 Eigen::Matrix3f I = Eigen::Matrix3f::Identity ();
  Eigen::Vector3f n_idx (normals[p_idx].normal[0], normals[p_idx].normal[1], normals[p_idx].normal[2]);
  EIGEN_ALIGN16 Eigen::Matrix3f M = I - n_idx * n_idx.transpose ();    // projection matrix (into tangent plane)

  // Project normals into the tangent plane
  Eigen::Vector3f normal;
  projected_normals_.resize (indices.size ());
  xyz_centroid_.setZero ();
  for (std::size_t idx = 0; idx < indices.size(); ++idx)
  {
    normal[0] = normals[indices[idx]].normal[0];
    normal[1] = normals[indices[idx]].normal[1];
    normal[2] = normals[indices[idx]].normal[2];

    projected_normals_[idx] = M * normal;
    xyz_centroid_ += projected_normals_[idx];
  }

  // Estimate the XYZ centroid
  xyz_centroid_ /= static_cast (indices.size ());

  // Initialize to 0
  covariance_matrix_.setZero ();

  // For each point in the cloud
  for (std::size_t idx = 0; idx < indices.size (); ++idx)
  {
    demean_ = projected_normals_[idx] - xyz_centroid_;

    double demean_xy = demean_[0] * demean_[1];
    double demean_xz = demean_[0] * demean_[2];
    double demean_yz = demean_[1] * demean_[2];

    covariance_matrix_(0, 0) += demean_[0] * demean_[0];
    covariance_matrix_(0, 1) += static_cast (demean_xy);
    covariance_matrix_(0, 2) += static_cast (demean_xz);

    covariance_matrix_(1, 0) += static_cast (demean_xy);
    covariance_matrix_(1, 1) += demean_[1] * demean_[1];
    covariance_matrix_(1, 2) += static_cast (demean_yz);

    covariance_matrix_(2, 0) += static_cast (demean_xz);
    covariance_matrix_(2, 1) += static_cast (demean_yz);
    covariance_matrix_(2, 2) += demean_[2] * demean_[2];
  }

  // Extract the eigenvalues and eigenvectors
  pcl::eigen33 (covariance_matrix_, eigenvalues_);
  pcl::computeCorrespondingEigenVector (covariance_matrix_, eigenvalues_ [2], eigenvector_);

  pcx = eigenvector_ [0];
  pcy = eigenvector_ [1];
  pcz = eigenvector_ [2];
  float indices_size = 1.0f / static_cast (indices.size ());
  pc1 = eigenvalues_ [2] * indices_size;
  pc2 = eigenvalues_ [1] * indices_size;
}

假若某点的曲率是 k1、k2，

平均曲率：表示的是弯曲测量标准，是对一个曲面嵌入周围空间（一个二维的曲面嵌入三维的欧式空间）的曲率进行了局部的描述

那么改点的平均曲率是：K=（k1+k2）/2

高斯曲率：描述的是曲面的凹凸性质的量，当两个量变化程度较大的时候表面曲面内部变化也是很大的。表示的是曲面的光滑程度。

同理该点的高斯曲率则是： K=k1*k2

2、表面曲率

表面曲率是点云数据表面的特征值来描述点云变幻程度一个概念。

二、曲率的计算

  方法一： 二次曲面拟合点云曲率

在散点的点云中随机的拿出一个点pi，然后以pi为中心点均匀的取n个点（最好是n个点能覆盖整个点云的边界和特征），然后使用最小二乘法拟合一个二次曲面方程：PCL 二次曲面拟合并计算曲率_Σίσυφος1900的博客-CSDN博客

  方法二： 利用相邻点的法向量求一个点的曲率

三、主曲率

#if 1  //  显示点云的 主曲率 

int   main()
{
            pcl::PointCloud::Ptr  m_current_cloud(new  pcl::PointCloud);
            if (-1 == pcl::io::loadPCDFile("Armadillo.pcd", *m_current_cloud))//放到与工程中的主.cpp同一位置的文件夹下
            {
                cout << "加载文件失败！" << endl;
                return -1;
            }
            cout << m_current_cloud->points.size() << endl;
            
            // 计算点云的法向量
            pcl::NormalEstimation n;
            n.setInputCloud(m_current_cloud);
            pcl::search::KdTree::Ptr tree(new pcl::search::KdTree );
            n.setSearchMethod(tree);

            n.setKSearch(20);

            // 定义一个新的点云来显示有法向量的值
            pcl::PointCloud::Ptr normals(new  pcl::PointCloud);
            n.compute(*normals);

            // 开始计算主曲率
            pcl::PrincipalCurvaturesEstimation < pcl::PointXYZ, pcl::Normal, pcl::PrincipalCurvatures > p;
            p.setInputCloud(m_current_cloud);
            p.setInputNormals(normals);   // 输入法向量
            p.setSearchMethod(tree);  //使用kd树的方法
            p.setKSearch(10);


            pcl::PointCloud::Ptr  pri(new pcl::PointCloud);
            p.compute(*pri);


            cout << "output points.size: " << pri->points.size() << endl;
            // 显示和检索第0点的主曲率。
            cout << "第0点最大主曲率;" << pri->points[0].pc1 << endl;// 输出最大曲率
            cout << "第0点最小主曲率:" << pri->points[0].pc2 << endl;// 输出最小曲率


            //输出主曲率方向（最大特征值对应的特征向量）
            cout << "第0点主曲率方向;" << endl;
            cout << pri->points[0].principal_curvature_x << endl;
            cout << pri->points[0].principal_curvature_y << endl;
            cout << pri->points[0].principal_curvature_z << endl;



            //  显示结果：
            boost::shared_ptr viewer(new pcl::visualization::PCLVisualizer("Normal viewer"));
            viewer->setBackgroundColor(0.3, 0.3, 0.3);     //设置背景颜色
            viewer->addText("Curvatures", 10, 10, "text"); //设置显示文字
            viewer->setWindowName("计算主曲率");           //设置窗口名字

            viewer->addCoordinateSystem(0.1);              //添加坐标系


            //设置点云颜色
            pcl::visualization::PointCloudColorHandlerCustom single_color(m_current_cloud, 0, 225, 0);
            //添加点云到可视化窗口
            viewer->addPointCloud(m_current_cloud, single_color, "cloud"); 
            //设置点云大小
            viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "cloud");


            //添加需要显示的点云法向。m_current_cloud为原始点云模型，normal为法向信息，20表示需要显示法向的点云间隔，即每20个点显示一次法向，2表示法向长度。
            viewer->addPointCloudNormals(m_current_cloud, normals, 20, 2, "normals");
            // 添加需要显示的点云主曲率。cloud为原始点云模型，normal为法向信息，pri为点云主曲率，
            // 10表示需要显示曲率的点云间隔，即每10个点显示一次主曲率，10表示法向长度。
            // 目前addPointCloudPrincipalCurvatures只接受和两个参数，未能实现曲率的可视化。
            viewer->addPointCloudPrincipalCurvatures(m_current_cloud, normals, pri, 10, 10, "Curvatures");

            while (!viewer->wasStopped())
            {
                viewer->spinOnce(100);
                boost::this_thread::sleep(boost::posix_time::microseconds(100000));
            }
            return 0;
   }
#endif

四、高斯曲率和平均曲率

#if 1  //  显示点云的 平均曲率  和高斯曲率
// 在这里我我们自定一个结构体来存储一个点的 高斯 和平均曲率
struct Curvature
{
    float Gaussian;
    float Mean;

};

int   main()
{
    pcl::PointCloud::Ptr  m_current_cloud(new  pcl::PointCloud);
    if (-1 == pcl::io::loadPCDFile("Armadillo.pcd", *m_current_cloud))//放到与工程中的主.cpp同一位置的文件夹下
    {
        cout << "加载文件失败！" << endl;
        return -1;
    }
    cout << m_current_cloud->points.size() << endl;

    // 计算点云的法向量
    pcl::NormalEstimation n;
    n.setInputCloud(m_current_cloud);
    pcl::search::KdTree::Ptr tree(new pcl::search::KdTree );
    n.setSearchMethod(tree);

    n.setKSearch(20);

    // 定义一个新的点云来显示有法向量的值
    pcl::PointCloud::Ptr normals(new  pcl::PointCloud);
    n.compute(*normals);

    // 开始计算主曲率
    pcl::PrincipalCurvaturesEstimation < pcl::PointXYZ, pcl::Normal, pcl::PrincipalCurvatures > p;
    p.setInputCloud(m_current_cloud);
    p.setInputNormals(normals);   // 输入法向量
    p.setSearchMethod(tree);  //使用kd树的方法
    p.setKSearch(10);


    pcl::PointCloud::Ptr  pri(new pcl::PointCloud);
    p.compute(*pri);


   
  // 输出点云中每个点的gauss  mean    min max  曲率
    float   k1 = 0.0;
    float   k2 = 0.0;
    Curvature cv = { 0.0,0.0 }; // 初始化结构体

    vector vc_kv;
    for (size_t i = 0; i < pri->points.size(); i++)
    {
        k1 = pri->points[i].pc1;  //  
        k2 = pri->points[i].pc2;
        cv.Gaussian = k1 * k2;
        cv.Mean = (k1 + k2) / 2;
        vc_kv.push_back(cv);
    }


    // 输出前10个点的高斯曲率和平均曲率
    for (size_t i = 0; i < 50; ++i)

        cout << "第" << i + 1 << "个点的高斯曲率为：" << vc_kv[i].Gaussian <<
        "\n平均曲率为：" << vc_kv[i].Mean << endl;

    //  显示结果：
    boost::shared_ptr viewer(new pcl::visualization::PCLVisualizer("Normal viewer"));
    viewer->setBackgroundColor(0.3, 0.3, 0.3);     //设置背景颜色
    viewer->addText("Curvatures", 10, 10, "text"); //设置显示文字
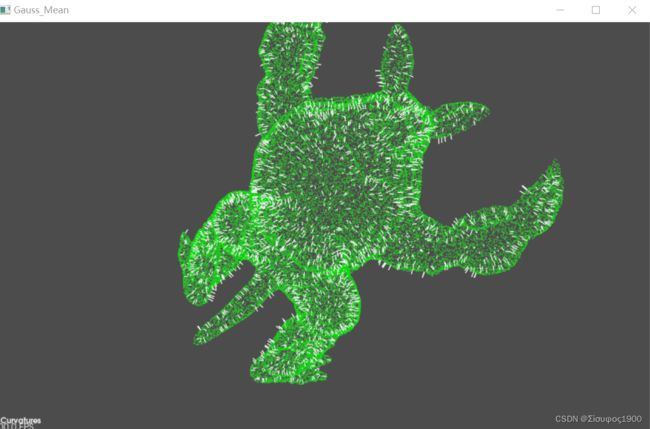
    viewer->setWindowName("Gauss_Mean");           //设置窗口名字
    viewer->addCoordinateSystem(0.1);              //添加坐标系


    //设置点云颜色
    pcl::visualization::PointCloudColorHandlerCustom single_color(m_current_cloud, 0, 225, 0);
    //添加点云到可视化窗口
    viewer->addPointCloud(m_current_cloud, single_color, "cloud");
    //设置点云大小
    viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "cloud");


    //添加需要显示的点云法向。m_current_cloud为原始点云模型，normal为法向信息，20表示需要显示法向的点云间隔，即每20个点显示一次法向，2表示法向长度。
    viewer->addPointCloudNormals(m_current_cloud, normals, 20, 2, "normals");
    // 添加需要显示的点云主曲率。cloud为原始点云模型，normal为法向信息，pri为点云主曲率，
    // 10表示需要显示曲率的点云间隔，即每10个点显示一次主曲率，10表示法向长度。
    // 目前addPointCloudPrincipalCurvatures只接受和两个参数，未能实现曲率的可视化。
    viewer->addPointCloudPrincipalCurvatures(m_current_cloud, normals, pri, 10, 10, "Curvatures");

    while (!viewer->wasStopped())
    {
        viewer->spinOnce(100);
        boost::this_thread::sleep(boost::posix_time::microseconds(100000));
    }
    return 0;
   }
#endif

 最大，最小， 高斯  平均 曲率：

49791
第1个点的高斯曲率为：4.06178e-07
平均曲率为：0.00161614
第2个点的高斯曲率为：0.00706714
平均曲率为：0.118564
第3个点的高斯曲率为：0.000544364
平均曲率为：0.033619
第4个点的高斯曲率为：0.00477594
平均曲率为：0.102736
第5个点的高斯曲率为：3.9182e-06
平均曲率为：0.00534493
第6个点的高斯曲率为：2.87925e-06
平均曲率为：0.00232935
第7个点的高斯曲率为：0.00516027
平均曲率为：0.0751841
第8个点的高斯曲率为：8.13437e-07
平均曲率为：0.00145573
第9个点的高斯曲率为：0.0160201
平均曲率为：0.13726
第10个点的高斯曲率为：0.00434192
平均曲率为：0.0998214
第11个点的高斯曲率为：9.45795e-06
平均曲率为：0.0107193
第12个点的高斯曲率为：0.00115901
平均曲率为：0.0643258
第13个点的高斯曲率为：0.00872426
平均曲率为：0.119462
第14个点的高斯曲率为：0.0029446
平均曲率为：0.0737549
第15个点的高斯曲率为：0.00332806
平均曲率为：0.0693298
第16个点的高斯曲率为：0.00296655
平均曲率为：0.0778702
第17个点的高斯曲率为：0.00510475
平均曲率为：0.0865642
第18个点的高斯曲率为：0.00122556
平均曲率为：0.0397958
第19个点的高斯曲率为：3.13014e-06
平均曲率为：0.00241366
第20个点的高斯曲率为：0.00324422
平均曲率为：0.0615579
第21个点的高斯曲率为：3.18268e-06
平均曲率为：0.00562428
第22个点的高斯曲率为：0.000986595
平均曲率为：0.0485682
第23个点的高斯曲率为：0.00713579
平均曲率为：0.0886364
第24个点的高斯曲率为：0.00403163
平均曲率为：0.0697144
第25个点的高斯曲率为：0.000717951
平均曲率为：0.0371761
第26个点的高斯曲率为：3.17172e-06
平均曲率为：0.00470309
第27个点的高斯曲率为：0.000153206
平均曲率为：0.0154591
第28个点的高斯曲率为：0.00464327
平均曲率为：0.0913673
第29个点的高斯曲率为：1.30676e-06
平均曲率为：0.00133414
第30个点的高斯曲率为：0.00224555
平均曲率为：0.0599507
第31个点的高斯曲率为：5.98324e-05
平均曲率为：0.00914722
第32个点的高斯曲率为：0.00271725
平均曲率为：0.0650881
第33个点的高斯曲率为：0.00705604
平均曲率为：0.10315
第34个点的高斯曲率为：0.00111071
平均曲率为：0.0689896
第35个点的高斯曲率为：1.86115e-06
平均曲率为：0.00150633
第36个点的高斯曲率为：8.31745e-07
平均曲率为：0.00188476
第37个点的高斯曲率为：2.755e-05
平均曲率为：0.00531796
第38个点的高斯曲率为：0.0262126
平均曲率为：0.228413
第39个点的高斯曲率为：2.04287e-05
平均曲率为：0.00555236
第40个点的高斯曲率为：7.19944e-06
平均曲率为：0.00374902
第41个点的高斯曲率为：0.000202232
平均曲率为：0.0550556
第42个点的高斯曲率为：0.00172058
平均曲率为：0.107448
第43个点的高斯曲率为：0.00105404
平均曲率为：0.0562264
第44个点的高斯曲率为：0.000223625
平均曲率为：0.0302091
第45个点的高斯曲率为：0.00255065
平均曲率为：0.0645522
第46个点的高斯曲率为：4.42084e-06
平均曲率为：0.00292578
第47个点的高斯曲率为：0.00130016
平均曲率为：0.0557482
第48个点的高斯曲率为：4.4202e-09
平均曲率为：0.000209263
第49个点的高斯曲率为：0.0152398
平均曲率为：0.158841
第50个点的高斯曲率为：0.000180538
平均曲率为：0.0603573