NNDL 实验五 前馈神经网络(3)鸢尾花分类
目录
深入研究鸢尾花数据集
4.5 实践:基于前馈神经网络完成鸢尾花分类
4.5.1 小批量梯度下降法
4.5.2 数据处理
4.5.2.2 用DataLoader进行封装
4.5.3 模型构建
4.5.4 完善Runner类
4.5.5 模型训练
4.5.6 模型性价
4.5.7 模型预测
思考题
实验总结
参考文献
深入研究鸢尾花数据集
画出数据集中150个数据的前两个特征的散点分布图:
![]()
4.5 实践:基于前馈神经网络完成鸢尾花分类
在本实践中,我们继续使用第三章中的鸢尾花分类任务,将Softmax分类器替换为本章介绍的前馈神经网络。
在本实验中,我们使用的损失函数为交叉熵损失;优化器为随机梯度下降法;评价指标为准确率。
4.5.1 小批量梯度下降法
为了减少每次迭代的计算复杂度,我们可以在每次迭代时只采集一小部分样本,计算在这组样本上损失函数的梯度并更新参数,这种优化方式称为小批量梯度下降法(Mini-Batch Gradient Descent,Mini-Batch GD)。
为了小批量梯度下降法,我们需要对数据进行随机分组。
目前,机器学习中通常做法是构建一个数据迭代器,每个迭代过程中从全部数据集中获取一批指定数量的数据。
4.5.2 数据处理
实验代码如下
import numpy as np
import torch
import torch.utils.data as io
from nndl.dataset import load_data
class IrisDataset(io.Dataset):
def __init__(self, mode='train', num_train=120, num_dev=15):
super(IrisDataset, self).__init__()
# 调用第三章中的数据读取函数,其中不需要将标签转成one-hot类型
X, y = load_data(shuffle=True)
if mode == 'train':
self.X, self.y = X[:num_train], y[:num_train]
elif mode == 'dev':
self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
else:
self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]
def __getitem__(self, idx):
return self.X[idx], self.y[idx]
def __len__(self):
return len(self.y)
torch.seed()
train_dataset = IrisDataset(mode='train')
dev_dataset = IrisDataset(mode='dev')
test_dataset = IrisDataset(mode='test')
打印训练集长度
# 打印训练集长度
print ("length of train set: ", len(train_dataset))输出结果
length of train set: 1204.5.2.2 用DataLoader进行封装
# 批量大小
batch_size = 16
# 加载数据
train_loader = io.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = io.DataLoader(test_dataset, batch_size=batch_size)4.5.3 模型构建
构建一个简单的前馈神经网络进行鸢尾花分类实验。其中输入层神经元个数为4,输出层神经元个数为3,隐含层神经元个数为6。代码实现如下:
from torch import nn
# 定义前馈神经网络
class Model_MLP_L2_V3(nn.Module):
def __init__(self, input_size, output_size, hidden_size):
super(Model_MLP_L2_V3, self).__init__()
# 构建第一个全连接层
self.fc1 = nn.Linear(
input_size,
hidden_size,
)
nn.init.normal_(self.fc1.weight, mean=0, std=0.01)
nn.init.constant_(self.fc1.bias,1.0)
# 构建第二全连接层
self.fc2 = nn.Linear(
hidden_size,
output_size,
)
nn.init.normal_(self.fc2.weight, mean=0, std=0.01)
nn.init.constant_(self.fc2.bias, 1.0)
# 定义网络使用的激活函数
self.act = nn.Sigmoid()
def forward(self, inputs):
outputs = self.fc1(inputs)
outputs = self.act(outputs)
outputs = self.fc2(outputs)
return outputs
fnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size=6)4.5.4 完善Runner类
基于RunnerV2类进行完善实现了RunnerV3类。其中训练过程使用自动梯度计算,使用DataLoader加载批量数据,使用随机梯度下降法进行参数优化;模型保存时,使用state_dict方法获取模型参数;模型加载时,使用set_state_dict方法加载模型参数.
由于这里使用随机梯度下降法对参数优化,所以数据以批次的形式输入到模型中进行训练,那么评价指标计算也是分别在每个批次进行的,要想获得每个epoch整体的评价结果,需要对历史评价结果进行累积。这里定义Accuracy类实现该功能。
RunnerV3类的代码实现如下:
class RunnerV3(object):
def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric # 只用于计算评价指标
# 记录训练过程中的评价指标变化情况
self.dev_scores = []
# 记录训练过程中的损失函数变化情况
self.train_epoch_losses = [] # 一个epoch记录一次loss
self.train_step_losses = [] # 一个step记录一次loss
self.dev_losses = []
# 记录全局最优指标
self.best_score = 0
def train(self, train_loader, dev_loader=None, **kwargs):
# 将模型切换为训练模式
self.model.train()
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_steps = kwargs.get("log_steps", 100)
# 评价频率
eval_steps = kwargs.get("eval_steps", 0)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
custom_print_log = kwargs.get("custom_print_log", None)
# 训练总的步数
num_training_steps = num_epochs * len(train_loader)
if eval_steps:
if self.metric is None:
raise RuntimeError('Error: Metric can not be None!')
if dev_loader is None:
raise RuntimeError('Error: dev_loader can not be None!')
# 运行的step数目
global_step = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
# 用于统计训练集的损失
total_loss = 0
for step, data in enumerate(train_loader):
X, y = data
# 获取模型预测
logits = self.model(X)
loss = self.loss_fn(logits, y) # 默认求mean
total_loss += loss
# 训练过程中,每个step的loss进行保存
self.train_step_losses.append((global_step, loss.item()))
if log_steps and global_step % log_steps == 0:
print(
f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
# 梯度反向传播,计算每个参数的梯度值
loss.backward()
if custom_print_log:
custom_print_log(self)
# 小批量梯度下降进行参数更新
self.optimizer.step()
# 梯度归零
optimizer.zero_grad()
# 判断是否需要评价
if eval_steps > 0 and global_step > 0 and \
(global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):
dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
print(f"[Evaluate] dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")
# 将模型切换为训练模式
self.model.train()
# 如果当前指标为最优指标,保存该模型
if dev_score > self.best_score:
self.save_model(save_path)
print(
f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
self.best_score = dev_score
global_step += 1
# 当前epoch 训练loss累计值
trn_loss = (total_loss / len(train_loader)).item()
# epoch粒度的训练loss保存
self.train_epoch_losses.append(trn_loss)
print("[Train] Training done!")
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def evaluate(self, dev_loader, **kwargs):
assert self.metric is not None
# 将模型设置为评估模式
self.model.eval()
global_step = kwargs.get("global_step", -1)
# 用于统计训练集的损失
total_loss = 0
# 重置评价
self.metric.reset()
# 遍历验证集每个批次
for batch_id, data in enumerate(dev_loader):
X, y = data
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
# 累积损失
total_loss += loss
# 累积评价
self.metric.update(logits, y)
dev_loss = (total_loss / len(dev_loader))
dev_score = self.metric.compute()
# 记录验证集loss
if global_step != -1:
self.dev_losses.append((global_step, dev_loss))
self.dev_scores.append(dev_score)
return dev_score, dev_loss
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def predict(self, x, **kwargs):
# 将模型设置为评估模式
self.model.eval()
# 运行模型前向计算,得到预测值
logits = self.model(x)
return logits
def save_model(self, save_path):
torch.save(self.model.state_dict(), save_path)
def load_model(self, model_path):
state_dict = torch.load(model_path)
self.model.load_state_dict(state_dict)4.5.5 模型训练
实例化RunnerV3类,并传入训练配置,代码实现如下:
lr = 0.2
# 定义网络
model = fnn_model
# 定义优化器
optimizer = opt.SGD(model.parameters(),lr, )
# 定义损失函数。softmax+交叉熵
loss_fn = F.cross_entropy
metric = Accuracy(is_logist=True)
runner = RunnerV3(model, optimizer, loss_fn, metric)
使用训练集和验证集进行模型训练,共训练150个epoch。在实验中,保存准确率最高的模型作为最佳模型。代码实现如下:
# 启动训练
log_steps = 100
eval_steps = 50
runner.train(train_loader, dev_loader,
num_epochs=150, log_steps=log_steps, eval_steps = eval_steps,
save_path="best_model.pdparams")训练结果
[Train] epoch: 0/150, step: 0/1200, loss: 1.10467
[Evaluate] dev score: 0.26667, dev loss: 1.22231
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.26667
[Train] epoch: 12/150, step: 100/1200, loss: 1.11286
[Evaluate] dev score: 0.26667, dev loss: 1.11308
[Evaluate] dev score: 0.26667, dev loss: 1.13753
[Train] epoch: 25/150, step: 200/1200, loss: 1.11455
[Evaluate] dev score: 0.26667, dev loss: 1.12687
[Evaluate] dev score: 0.26667, dev loss: 1.11112
[Train] epoch: 37/150, step: 300/1200, loss: 1.07319
[Evaluate] dev score: 0.26667, dev loss: 1.09228
[Evaluate] dev score: 0.26667, dev loss: 1.07941
[Train] epoch: 50/150, step: 400/1200, loss: 0.96820
[Evaluate] dev score: 0.53333, dev loss: 1.02344
[Evaluate] best accuracy performence has been updated: 0.26667 --> 0.53333
[Evaluate] dev score: 0.53333, dev loss: 0.93751
[Train] epoch: 62/150, step: 500/1200, loss: 0.72586
[Evaluate] dev score: 0.60000, dev loss: 0.77080
[Evaluate] best accuracy performence has been updated: 0.53333 --> 0.60000
[Evaluate] dev score: 0.66667, dev loss: 0.67423
[Evaluate] best accuracy performence has been updated: 0.60000 --> 0.66667
[Train] epoch: 75/150, step: 600/1200, loss: 0.53801
[Evaluate] dev score: 0.86667, dev loss: 0.57472
[Evaluate] best accuracy performence has been updated: 0.66667 --> 0.86667
[Evaluate] dev score: 0.80000, dev loss: 0.56176
[Train] epoch: 87/150, step: 700/1200, loss: 0.38122
[Evaluate] dev score: 0.86667, dev loss: 0.50781
[Evaluate] dev score: 0.93333, dev loss: 0.46224
[Evaluate] best accuracy performence has been updated: 0.86667 --> 0.93333
[Train] epoch: 100/150, step: 800/1200, loss: 0.43660
[Evaluate] dev score: 0.93333, dev loss: 0.43534
[Evaluate] dev score: 1.00000, dev loss: 0.40225
[Evaluate] best accuracy performence has been updated: 0.93333 --> 1.00000
[Train] epoch: 112/150, step: 900/1200, loss: 0.33995
[Evaluate] dev score: 0.93333, dev loss: 0.38908
[Evaluate] dev score: 0.93333, dev loss: 0.36191
[Train] epoch: 125/150, step: 1000/1200, loss: 0.28941
[Evaluate] dev score: 1.00000, dev loss: 0.33070
[Evaluate] dev score: 1.00000, dev loss: 0.31569
[Train] epoch: 137/150, step: 1100/1200, loss: 0.27491
[Evaluate] dev score: 1.00000, dev loss: 0.30810
[Evaluate] dev score: 1.00000, dev loss: 0.28763
[Evaluate] dev score: 1.00000, dev loss: 0.26681
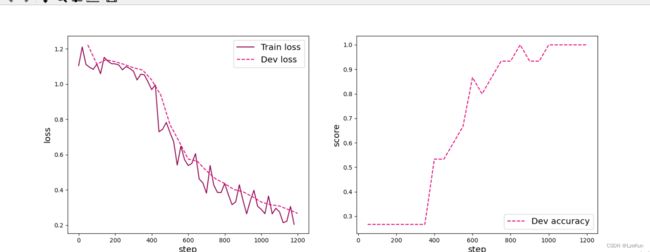
[Train] Training done!# 绘制训练集和验证集的损失变化以及验证集上的准确率变化曲线
def plot_training_loss_acc(runner, fig_name,
fig_size=(16, 6),
sample_step=20,
loss_legend_loc="upper right",
acc_legend_loc="lower right",
train_color="#e4007f",
dev_color='#f19ec2',
fontsize='large',
train_linestyle="-",
dev_linestyle='--'):
plt.figure(figsize=fig_size)
plt.subplot(1, 2, 1)
train_items = runner.train_step_losses[::sample_step]
train_steps = [x[0] for x in train_items]
train_losses = [x[1] for x in train_items]
plt.plot(train_steps, train_losses, color=train_color, linestyle=train_linestyle, label="Train loss")
if len(runner.dev_losses) > 0:
dev_steps = [x[0] for x in runner.dev_losses]
dev_losses = [x[1] for x in runner.dev_losses]
plt.plot(dev_steps, dev_losses, color=dev_color, linestyle=dev_linestyle, label="Dev loss")
# 绘制坐标轴和图例
plt.ylabel("loss", fontsize=fontsize)
plt.xlabel("step", fontsize=fontsize)
plt.legend(loc=loss_legend_loc, fontsize='x-large')
# 绘制评价准确率变化曲线
if len(runner.dev_scores) > 0:
plt.subplot(1, 2, 2)
plt.plot(dev_steps, runner.dev_scores,
color=dev_color, linestyle=dev_linestyle, label="Dev accuracy")
# 绘制坐标轴和图例
plt.ylabel("score", fontsize=fontsize)
plt.xlabel("step", fontsize=fontsize)
plt.legend(loc=acc_legend_loc, fontsize='x-large')
plt.savefig(fig_name)
plt.show()从输出结果可以看出准确率随着迭代次数增加逐渐上升,损失函数下降。
4.5.6 模型性价
使用测试数据对在训练过程中保存的最佳模型进行评价,观察模型在测试集上的准确率以及Loss情况。代码实现如下:
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))[Test] accuracy/loss: 1.0000/0.15644.5.7 模型预测
同样地,也可以使用保存好的模型,对测试集中的某一个数据进行模型预测,观察模型效果。代码实现如下:
# 获取测试集中第一条数据
#print(test_loader)
for i_batch, batch_data in enumerate(test_loader):
print(i_batch) # 打印batch编号
print(batch_data[0].size()) # 打印该batch里面src
print(batch_data[1].size()) # 打印该batch里面trg
X, label = batch_data[0],batch_data[1],
logits = runner.predict(X)
pred_class = torch.argmax(logits[0])
label = label[0]
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))The true category is 2 and the predicted category is 2思考题
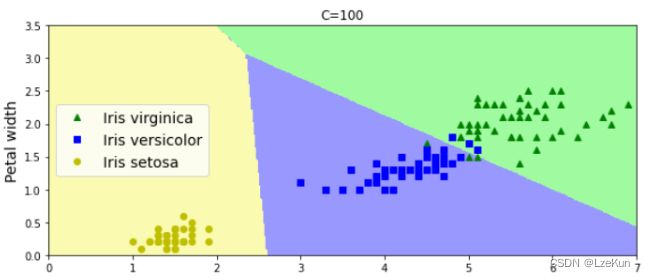
1、对比Softmax分类和前馈神经网络分类。(必做)
# coding=gbk
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from matplotlib.colors import ListedColormap
iris = datasets.load_iris() # 加载数据
list(iris.keys()) # ['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module']
X = iris["data"][:, 3:] # 花瓣长度
y = (iris["target"] == 2).astype(np.int32) # 标签,是维吉尼亚鸢尾花y就是1,否则为0
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y) # 训练模型
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 4.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
X = iris["data"][:, (2, 3)] # 花瓣长度, 花瓣宽度
y = iris["target"]
# 设置超参数multi_class为"multinomial",指定一个支持Softmax回归的求解器,默认使用l2正则化,可以通过超参数C进行控制
softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=1, random_state=42)
softmax_reg.fit(X, y)
softmax_reg.predict([[5, 2]]) # 输出:array([2])
softmax_reg.predict_proba([[5, 2]])
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(8, 3))
plt.plot(X[y == 2, 0], X[y == 2, 1], "g^", label="Iris virginica")
plt.plot(X[y == 1, 0], X[y == 1, 1], "bs", label="Iris versicolor")
plt.plot(X[y == 0, 0], X[y == 0, 1], "yo", label="Iris setosa")
custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=13)
plt.ylabel("Petal width", fontsize=13)
plt.legend(loc="center left", fontsize=13)
plt.axis([0, 7, 0, 3.5])
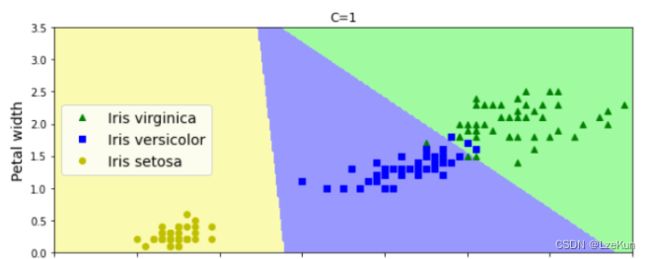
plt.title('C=1')
plt.show()
实验总结
图来自 《机器学习5:神经网络 》脑图_huoren_的博客-CSDN博客
本次实验实践了基于前馈神经网络完成鸢尾花分类任务。从paddle转化为pytorch过程中出现了一些问题,存在问题还很多,学习过程任重而道远。。。
参考文献
【统计学习方法】感知机对鸢尾花(iris)数据集进行二分类--鸢尾花散点图
《机器学习5:神经网络 》脑图