深度学习导航（一）——神经网络的定义和基本概念
文章目录
- 引子
- 1.人工神经网络的定义和基本运算
-
- 1.1人工神经网络的定义
- 1.2神经网络的基本运算
- 2.关于神经网络的一些基本概念
-
- 2.1激活函数
- 2.2正向传播与反向传播
-
- 2.2.1正向传播
- 2.2.2反向传播
- 2.3梯度下降法
- 2.4过拟合和欠拟合
-
- 2.4.1过拟合
- 2.4.2欠拟合
- 总结
- 参考
引子
接触深度学习有一段时间了，最近浅浅学习了一下神经网络相关内容，对理论有了更多的理解。这里想到做一个适合深度学习小白的导航式入门教程，让大家快速了解神经网络的最基本内容和最突出的特点，考虑到非科班出身资历尚浅，数学推导的内容基本不涉及，主要是帮助大家对各种神经网络有一个总体的认知，以我之见非科班出身的本科同学在应用层面做些小科创应该够了。
下面很多概念是普适于机器学习领域的，但也有些概念仅限于深度学习。本教程以深度学习为主要导向。
1.人工神经网络的定义和基本运算
1.1人工神经网络的定义
大家都知道人脑具有神经网络，也即生物神经网络，借助它人们可以完成思考、信息处理等重要生活内容。顾名思义，人工神经网络就是人为设定的、用数学模型实现的神经网络，它可以让计算机、没有生命的机器拥有类似于人类甚至超过人类的生物智能。
人工神经网络是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象， 建立某种简单模型，按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。
1.2神经网络的基本运算
如图所示是一个基本神经元的输入和输出。
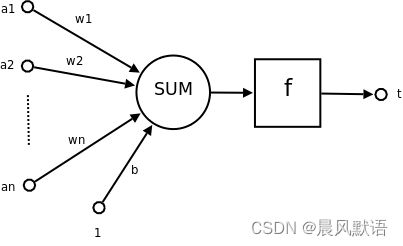
其运算分为以下几步：
1.输入值a1、a2、…an；
2.输入值乘上各自权重再求和：a1×w1 + a2×w2 + … + an×wn
3.加上偏置值b：a1×w1 + a2×w2 + … + an×wn + b
4.经过激活函数f()得到:f(a1×w1 + a2×w2 + … + an×wn + b),即输出y（图上最右边有点残缺哈）
激活函数在下一小节会具体说明。
直观的构造上是不是和生物神经元非常相似？
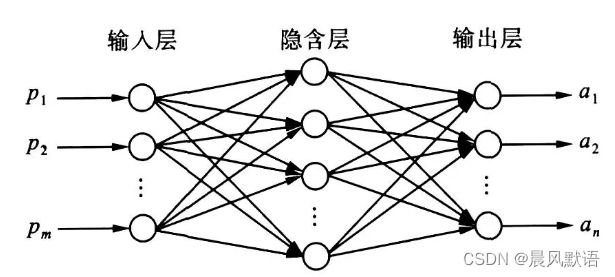
神经网络可以理解为由无数个神经元有机组合搭建成的网络，它有非常多的“层数”（一般由网络深度定义，定义为不包括输入层的层数）：
如图所示，一个神经元的输出可能作为多个神经元的输入，一个神经元的输入可能由多个神经元的输出构成。
以深度学习为例，图像分类、目标检测的相关网络就是将标注过的图像提取出输入值，输入到神经网络中，比对输出值和标注的真值差异，调整模型参数（即自监督式学习），最终达到一个参数收敛、模型正常拟合的程度。
2.关于神经网络的一些基本概念
2.1激活函数
激活函数有很多种，作为入门只讲最简单的sigmoid函数：
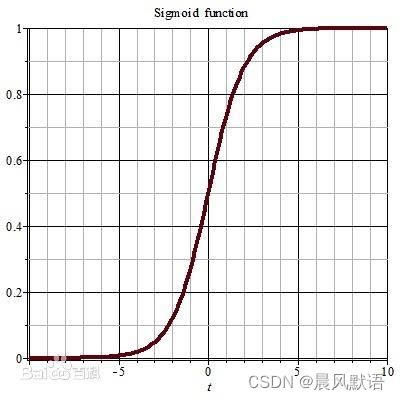
一看形状有点熟悉，其实高中就见过它了，人教版生物必修三的种群生长曲线中的“S型增长曲线”其实就是它，区别是这里的sigmoid函数值都集中在(0，1)之间。
可以想见它的作用就是把输入值压缩到（0，1）之间（又称“归一化”），这样做是为了防止某个神经元的输出值过大，作为下一个神经元的输入时将其他输入值的影响碾压得微乎其微，容易使模型过拟合。
当然激活函数还有其他作用，如减少参数计算量、加速模型收敛等。
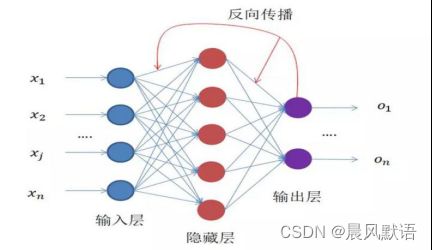
2.2正向传播与反向传播
2.2.1正向传播
简单来说，就是从输入→隐含层运算→输出的一个正向过程，深度学习训练时就是从图像中提取特征参数作为输入，经过模型初始设定的参数进行运算推理得到输出值。
2.2.2反向传播
正向传播得到输出值之后，会通过已设定好的损失值Loss计算方法（表示输出值与标注的真值之间的差异，简单可理解为误差，有多种设定方式）计算出损失值。
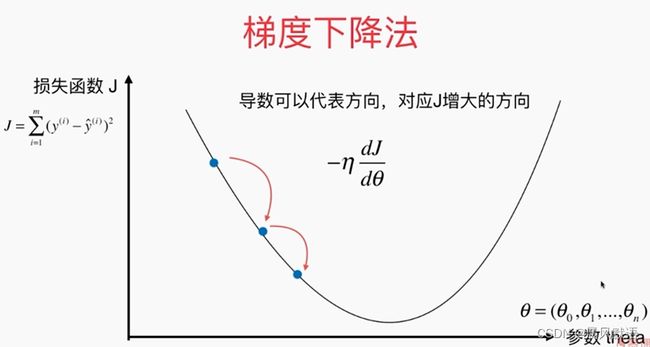
经过一定训练后，可以得到损失值关于网络参数的函数（即损失函数）：
如图是只考虑一个参数w1时的损失函数demo。
训练其实就是一个不断减小误差的过程，我们要肯定追求更小的loss值，因此产生了反向传播。我们通过一定的方法找到损失函数极小值处所对应的参数值，然后回到前面的网络中去调整这些参数来降低loss（使模型进一步收敛），这是一个由输出端返回到网络前层的过程，称为反向传播。
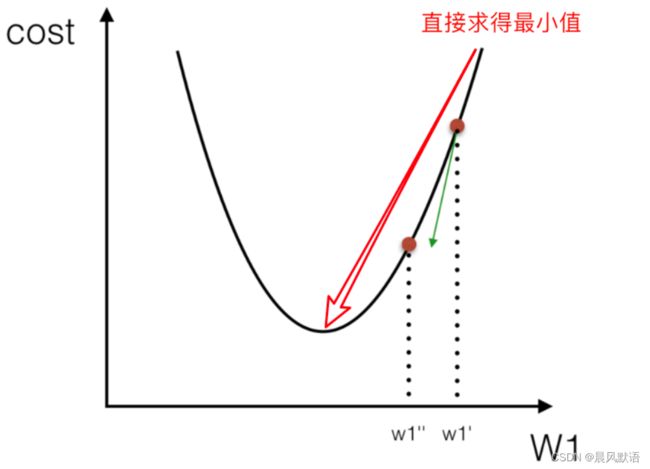
2.3梯度下降法
既然已经提到反向传播，那不得不提一嘴梯度下降法了。
上述得到损失函数Loss后，怎么求到它的极小值呢？高等数学大家都学过梯度的概念，梯度表示“函数值增加最快的方向”，那么梯度的反方向就是“函数值下降最快的方向”。想要用最快的速度去寻找极小值，当然得用最快的方式去寻找它，即沿着梯度的反向（图上直观看即是下降的最陡峭的方向）寻找，叫做“梯度下降法”。网上很多大佬的教程都以“人下山的过程”形象直观地体现梯度下降，确实就好比人沿着最陡峭的方向下山耗时最短一样。
但是我之前在学习梯度下降法时进入一个误区，这里还有一个概念是“学习率（learning rate，简称lr）下降”，我曾把学习率下降当成梯度下降…
学习率可以理解为是梯度下降的步长，即在某个点出计算出梯度，沿着梯度反方向向下走时，走一次跨多远的概念。梯度是针对某个点而言的，但下降时不可能经过每个点（loss函数本身通常是连续的），这里就涉及到了步长的选择。
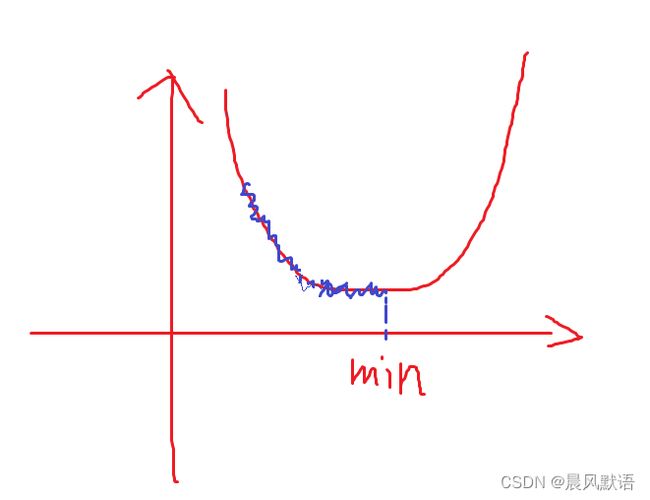
学习率如果设定得太大，那么下降时可能会直接跳过极小值点，并且在极小值附近不断震荡：
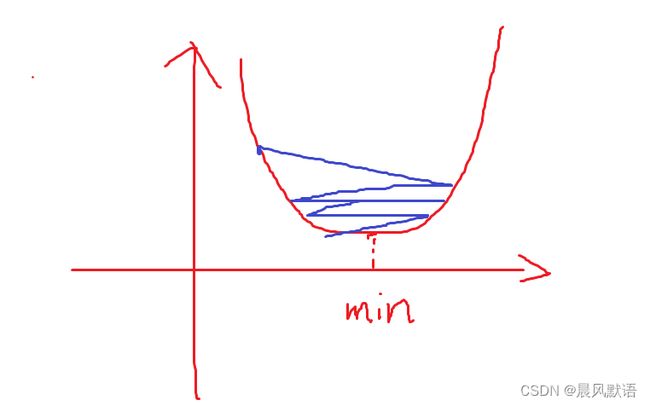
但学习率如果设定太小，极小值确实可以找到，但过程将十分缓慢：
因此我们可以选择，前期学习率设定大一些，而后学习率逐渐减小，这样可以兼得速度和准确度。
常见的梯度下降法包括随机梯度下降法（SGD）、批梯度下降法、Momentum梯度下降法、Nesterov Momentum梯度下降法、AdaGrad梯度下降法、RMSprop梯度下降法、Adam梯度下降法等。大家感兴趣的可以去仔细了解。
2.4过拟合和欠拟合
2.4.1过拟合
突然想到一张经典老图：
这里描述的就是过拟合的情况。
过拟合就是模型充分学习了训练集上的样本数据，但学的有点过头而且钻牛角尖，到真正让模型预测没见过的内容时效果就很差，即模型的泛化能力很差。好比一个学生刷题，刷的题已经完全弄懂而且很熟练，但是做新题又不会做。
过拟合有很多可能的诱因，比如数据量太少（刷题太少，题一变就不会）、网络拟合方式设定不佳（刷题方法不对）、数据集噪音太大或图像某项特征过于集中（刷的题质量不行或考察知识点非常有限）等。
2.4.2欠拟合
欠拟合更加严重，即不仅预测效果差，本身训练时的loss值也居高不下，模型参数并没有收敛到一个合适的值。
这一般是神经网络复杂度、深度不够导致的，当然也有可能是数据集成分过于复杂，给神经网络整不会了属于是，还有训练时间过短。一般来说，如果选择官方深度学习平台（pytorch、tensorflow、paddlepaddle等）给出的现成Architecture是不会出现欠拟合的问题的。
总结
这一节简单介绍了神经网络的基本定义、运算方法和一些常用基本概念，下一节讲解DNN、RNN、CNN等网络结构的各自特点。
如有讲的不对的地方，恳请大佬批评指正。
一些细节可以参考下面的链接：
参考
人工神经网络的概念：
https://baike.baidu.com/item/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/382460?fr=aladdin
神经网络的基本运算方法：
https://www.sohu.com/a/303882774_100254309
Sigmoid函数：
https://baike.baidu.com/item/Sigmoid%E5%87%BD%E6%95%B0/7981407?fr=aladdin
梯度下降法：
https://zhuanlan.zhihu.com/p/112416130?ivk_sa=1024320u
过拟合和欠拟合：
https://blog.csdn.net/qq_43211132/article/details/106937846