python 实现Fisher线性判别实例
基于Fisher准则的线性分类器设计
已知有两类数据和二者的先验概率,已知P(w1)=0.6,P(w2)=0.4。
W1和W2类数据点的对应坐标分别为:
x1=0.23 1.52 0.65 0.77 1.05 1.19 0.29 0.25 0.66 0.56 0.90 0.13 -0.54 0.94 -
0.21 0.05 -0.08 0.73 0.33 1.06 -0.02 0.11 0.31 0.66
y1=2.34 2.19 1.67 1.63 1.78 2.01 2.06 2.12 2.47 1.51 1.96 1.83 1.87 2.29 1.77
2.39 1.56 1.93 2.20 2.45 1.75 1.69 2.48 1.72
x2=1.40 1.23 2.08 1.16 1.37 1.18 1.76 1.97 2.41 2.58 2.84 1.95 1.25 1.28 1.26
2.01 2.18 1.79 1.33 1.15 1.70 1.59 2.93 1.46
y2=1.02 0.96 0.91 1.49 0.82 0.93 1.14 1.06 0.81 1.28 1.46 1.43 0.71 1.29 1.37
0.93 1.22 1.18 0.87 0.55 0.51 0.99 0.91 0.71
1)利用上面数据确定并画出Fisher判别准则下的最优投影方向,给出分类阈值。
2)根据所得结果判断(1,1.5)(1.2,1.0),(2.0,0.9),(1.2,1.5),(0.23,
2.33),属于哪类,并画出数据分类相应的结果图,要求画出其在W上的投影。
公式参考模式识别(张学工第三版)


最佳投影方向

分类阈值考虑先验概率
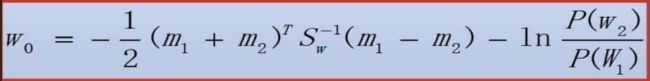
决策规则

在程序中修改为与w0作比较,就是移一下项。
具体代码如下
import numpy as np
import math
import matplotlib.pyplot as plt
x1=[0.23,1.52,0.65,0.77,1.05,1.19,0.29,0.25,0.66,0.56,0.90,0.13,-0.54,0.94,-0.21,0.05,-0.08,0.73,0.33,1.06,-0.02,0.11,0.31,0.66]
y1=[2.34,2.19,1.67,1.63,1.78,2.01,2.06,2.12,2.47,1.51,1.96,1.83,1.87,2.29,1.77,2.39,1.56,1.93,2.20,2.45,1.75,1.69,2.48,1.72]
x2=[1.40,1.23,2.08,1.16,1.37,1.18,1.76,1.97,2.41,2.58,2.84,1.95,1.25,1.28,1.26,2.01,2.18,1.79,1.33,1.15,1.70,1.59,2.93,1.46]
y2=[1.02,0.96,0.91,1.49,0.82,0.93,1.14,1.06,0.81,1.28,1.46,1.43,0.71,1.29,1.37,0.93,1.22,1.18,0.87,0.55,0.51,0.99,0.91,0.71]
#将矩阵整合为w1、w2
w1=[[0 for i in range(2)]for i in range(24)]
w2=[[0 for i in range(2)]for i in range(24)]
for i in range(24):
w1[i][0]=x1[i]
w1[i][1]=y1[i]
w2[i][0]=x2[i]
w2[i][1]=y2[i]
print('整合矩阵w1 w2')
print(w1)
print(w2)
#计算两类均值向量
m1=np.mean(w1,0)#mean(matrix,axis=0),matrix填写一个矩阵,axis 0代表:压缩行,对各列求均值
m2=np.mean(w2,0)#axis 1代表:压缩列,对各行求均值
print('计算两类均值向量')
print(m1)
print(m2)
#计算总的类内离散度矩阵Sw=s1+s2
s10=[0,0]
s20=[0,0]
s1=[[0 for i in range(2)]for j in range(2)]#2*2
s2=[[0 for i in range(2)]for j in range(2)]
for i in range(24):#这里要注意矩阵的转置
s10[0]=(w1[i][0]-m1[0])
s10[1]=(w1[i][1]-m1[1])
s11=np.mat(s10)#将list变为矩阵
s1+=np.mat((s11.T)*s11)#这里和书上公式相反,因为设置的时候和书上不一样,想到得到2*2的矩阵就必须换个方向
s20[0]=(w2[i][0]-m2[0])
s20[1]=(w2[i][1]-m2[1])
s22=np.mat(s20)
s2+=np.mat((s22.T)*s22)
print('s1')
print(s1)
print('s2')
print(s2)
sw=s1+s2
print('sw')
print(sw)
#计算投影方向和阈值
w_new=(np.mat(sw)).I*(np.mat((m1-m2)).T)
print('w_new')
print(w_new)
#这里因为考虑先验概率
m1_new=m1*w_new#这里的顺序很重要,因为前面设置的时候没有注意,所以写的时候要注意一下
m2_new=m2*w_new
pw1=0.6
pw2=0.4
w0=(m1_new+m2_new)/2-math.log(pw1/pw2)/(24+24-2)
print('w0')
print(w0)
#对测试数据进行分类判别
x=[[1,1.5],[1.2,1.0],[2.0,0.9],[1.2,1.5],[0.23,2.33]]
result1=[]
result2=[]
for i in range(5):
y=np.mat(x[i])*w_new#这里的顺序依然要小心
if y>w0[0][0]:
result1.append(x[i])
else:
result2.append(x[i])
print('result1')
print(result1)
print('result2')
print(result2)
#计算试验点在w_new方向上的点
w_k=np.mat(np.zeros((2,1)))#归一化
w_k[0]=w_new[0]/(np.linalg.norm(w_new,ord=2,axis=None,keepdims=False))#使用二范数进行归一化
w_k[1]=w_new[1]/(np.linalg.norm(w_new,ord=2,axis=None,keepdims=False))
print(w_k)
wd=np.mat(np.zeros((2,5)))
for i in range(5):
wd[:,i]=(np.mat(x[i])*(w_k*w_k.T)).T
print('wd')
print(wd)
#显示分类结果
mw1=np.mat(w1)
mw2=np.mat(w2)
mr1=np.mat(result1)
mr2=np.mat(result2)
p1=plt.scatter(mw1[:,0].tolist(),mw1[:,1].tolist(),c='red',marker='+')#画出w1类的各点
p2=plt.scatter(mw2[:,0].tolist(),mw2[:,1].tolist(),c='green',marker='s')#画出w2类的各点
p3=plt.scatter(mr1[:,0].tolist(),mr1[:,1].tolist())#画出测试集中属于w1的各点
p4=plt.scatter(mr2[:,0].tolist(),mr2[:,1].tolist())#画出测试集中属于w2的各点
p5=plt.plot([0,10*w_new[0]],[0,10*w_new[1]])#画出最佳投影方向
p6=plt.scatter(wd.T[:,0].tolist(),wd.T[:,1].tolist(),c='g',marker='*')#画出测试集各点在投影方向上的投影点
plt.legend([p1,p2,p3,p4,p6],['w1','w2','result1','result2','lx'])
#plt.legend([p5],['line'])
plt.show()

