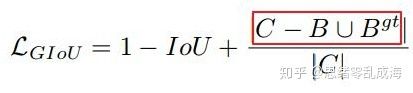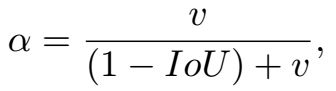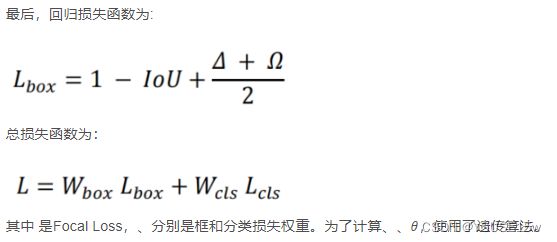目标检测中的损失函数

和图像分割中将损失函数分为基于分布，基于区域以及基于边界的损失函数不一样，目标检测经常可以认为由2类最基础的损失，分类损失(类别损失）和回归损失（位置损失）组成。

分类损失
CE loss，交叉熵损失

CE/BCE（cross entropy/ binary cross entropy）
交叉熵损失，二分类损失（binary CE loss）是它的一种极端情况. 在机器学习部分就有介绍它。
如下图所示,y是真实标签，a是预测标签，一般可通过sigmoid，softmax得到，x是样本，n是样本数目，和对数似然等价。

对于二分类来说

focal loss, 

focal loss出于论文Focal Loss for Dense Object Detection，主要是为了解决one-stage目标检测算法中正负样本比例严重失衡的问题，降低了大量简单负样本在训练中所占的比重，可理解为是一种困难样本挖掘。focal loss是在交叉熵损失函数上修改的。具体改进：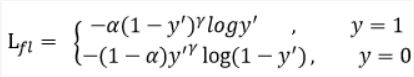

其中γ>0(文章中取2）使得减少易分类样本的损失，更关注困难的、错分的样本。例如γ为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的γ次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。
此外加入平衡因子α，用来平衡正负样本本身的比例不均，文中取值为0.25，即正样本比负样本占比小，这是因为负例易分。

 用改变loss的方式来缓解样本的不平衡，因为改变loss只影响train部分的过程和时间，而对推断时间影响甚小，容易拓展。
focal loss就是把CE里的p替换为pt，当预测正确的时候，pt接近1，在FL(pt)中，其系数越小（只要γ > 0 ）；简而言之，就是简单的样例比重越小，难的样例比重相对变大

 

 

Rankings类型的损失
在这有两类，DR(Distributional Ranking) Loss和AP Loss

DR Loss, 分布排序损失， Qian et al., 2020, DR loss: Improving object detection by distributional ranking
DR loss的研究背景和focal loss一样，one-stage方法中样本不平衡。它进行分布的转换以及用ranking作为loss。将分类问题转换为排序问题，从而避免了正负样本不平衡的问题。同时针对排序，提出了排序的损失函数DR loss。具体流程可参考：知乎链接

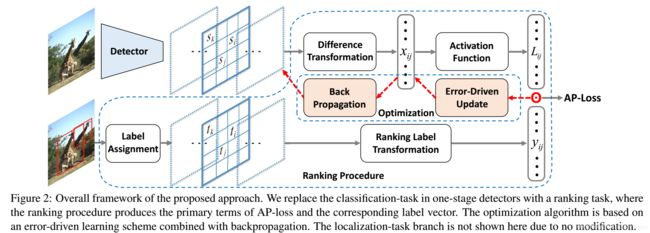
AP Loss, Chen et al., 2019, Towards Accurate One-Stage Object Detection with AP-Loss
AP loss也是解决one-stage方法中样本不平衡问题,同时也和DR loss类似，是一种排序loss。将单级检测器中的分类任务替换为排序任务，并采用平均精度损失(AP-loss)来处理排序问题。由于AP-loss的不可微性和非凸性，使得APloss不能直接优化。因此，本文开发了一种新的优化算法，它将感知器学习中的错误驱动更新方案和深度网络中的反向传播机制无缝地结合在一起。具体可参见：CSDN链接

 

目标检测的预测框回归损失函数由Classificition Loss和Bounding Box Regeression Loss两部分构成，本文介绍Bounding Box Regeression Loss。

Smooth L1 Loss-> IoU Loss（2016）-> GIoU Loss（2019）-> DIoU Loss（2020）->CIoU Loss（2020）

回归损失

0.MSE， RMSE，同样在机器学习中也会用来做回归损失。
常用在回归任务中，MSE的特点是光滑连续，可导，方便用于梯度下降。因为MSE是模型预测值 f(x) 与样本真实值 y 之间距离平方的平均值，故离得越远，误差越大，即受离群点的影响较大

 

1. L1 loss
L1 loss也称为平均绝对误差MAE （mean average error），即真实值和预测值差值的绝对值(计算得到的是各个样本输入得到的结果相对于对应的标签的差的绝对值，这也是计算误差最直观最简单的方法，输出结果和标签差了多少，我们就记多少误差。)：

从数学计算角度看，MAE的结果就是残差的平均值。例如有3个西瓜样本的数据x1，x2，x3，每个样本都是一个5维的数据，即：[大小，花纹宽度，重量，颜色深度，拍击是否有回响] ，标签分别为30%，60%，90%将他们输入一个神经网络，希望该神经网络输出的信息为西瓜的甜度；那么，假设该网络对应三个输入的输出值分别为25%，55%，96%，计算其MAE就得到损失值为16/3=5.33。从损失函数这个取名我们也可以看出，其含义就是对于每一个和标签不同的输出，将会产生多少的误差（损失）。

对于目标检测网络，我们要输出目标框的位置（x,y,w,h）和分类，因此标签也需要有对应的5个值。若采用MAE来计算损失函数，那么就是在一个batch结束后，分别统计每个待估值（需要得到的预测值）对于该batch各个样本的平均绝对误差，让损失函数对xi求偏导再将得到的结果作为反向传播的初始值，进行BP训练。分类只有是和不是，因此是一个二元的损失，但你仍然可以使用MAE作为分类损失函数，虽然它不是太好用。MAE还有一个缺点，就是在原点处不可导。

 设y-f(x)为横轴，MAE值为纵轴，函数图像如下：

 由图可知，L1损失函数对y-f(x)的导数为常数，在训练后期，即y与f(x)接近时，也即y-f(x)很小时，假设learning rate不变，损失函数会在稳定值附近波动，由于梯度的稳定，不利于模型收敛，很难收敛到更高的精度。

2. L2 loss

L2 loss也称为均方误差，即真实值和预测值差值的平方：

• RMSE和MAE的区别就在于，他会将误差求平方之后再求平均并在最后开方。

我们之前已经提到过，设计不同的、有针对性的损失函数是神经网络改进的关键，那么RMAE相对MAE又有什么改进呢？可以看到，MAE对于不同的样本的损失采取的策略是“一视同仁”，即不论单个样本产生的损失值有多大，最后都是获得相同的权重。对于那些损失小的样本，我们会认为该样本网络已经学习得比较好，不需要在这些样本上花费过多的精力；而对于损失值较大的样本，更应该“照顾有加”。那么有没有什么办法实现这种操作？铺垫了这么多，RMAE肯定就是一种能实现该需求的损失函数。每个样本在最终损失中的贡献会随着该样本损失的增大而增大（取了平方，不再是线性关系，相当于y=x^2和y=x比较）。因此RMAE会对训练得不好得样本施以更大的惩罚。但是同样，对于离群值（在这里是特别大的异常值）将会有一个巨大的损失，这将会误导模型的训练，MAE就没有这个问题。

设y-f(x)为横轴，MSE值为纵轴，函数图像如下：

由图可知，L2 loss函数处处可导，由于存在平方运算，当损失值大于1时，误差将会被放大；损失小于1时，误差将会被缩小，L2损失函数对y-f(x)的导数在y-f(x)值很大时，其导数也非常大，在训练前期不稳定，会造成模型的最终效果不太好。

缺点：
a、L1 Loss对x的导数为常数，由于 x 代表真实值与预测值的差值，故在训练后期x 很小时，如果学习率不变收敛很慢。
b、L2 Loss 在 x 值很大时，其导数非常大，故在训练初期不稳定。

3. smooth L1 loss

Smooth L1 由微软rgb大神提出，完美避开了L1和L2损失函数的缺点。
总结上述两种loss的缺点，smooth L1 loss改善L1 loss中的不可导点和梯度过于稳定的情况以及L2 loss中y-f(x)过大时梯度也很大的问题：

 其中，为真实值与预测值的差值，Smooth L1对x的导数为：

实际使用时：

其中，表示真实框坐标，表示预测的框坐标，即分别求出4个点的loss然后相加作为Bounding Box Regression Loss；

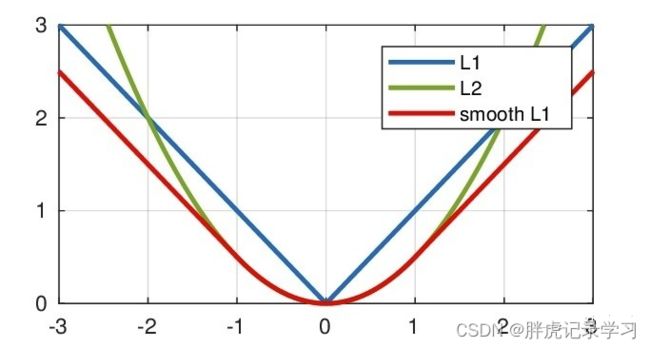
L1、L2、smooth l1三者的函数图像如下：

由图可知，smooth L1分别继承了L1和L2的优点：在损失大即当预测框与ground truth差别过大时的情况下，梯度不至于太大，损失小即当预测框与ground truth差别过小时的情况下，梯度足够小， 相比于L1损失函数，smooth L1可以收敛得更快，相比于L2损失函数，smooth L1对离散点、异常值不敏感，梯度变化相对更小；

Smooth L1 Loss在计算目标检测的bbox loss时，都是独立的求出4个点的loss然后相加得到最终的bbox loss，即默认4个点是相互独立的，假设坐标之间是没有相关性的，这与实际情况不符，例如当(x,y)位于图片右上角时，此时w=0，h=c。

缺点：
1、评价检测框的指标是使用的是IOU，但是和Smooth L1并不等价，多个检测框可能有相同的Loss但是IOU差异很大，此时引入了IOU Loss。
2、L1、L2、smooth Loss在计算bbox loss时，都是独立的求出4个点的loss，然后相加得到bbox loss。这种做法默认是4个点相互独立的。
 

4. IoU（Intersection over Union，交并比） loss

论文地址：

《UnitBox: An Advanced Object Detection Network (ACM-MM2016)》

在2016年由旷视提出，考虑重叠面积，归一化坐标尺度
IOU Loss：预测框和真实框之间的交集并集之比，用来确定正样本和负样本，评价预测框和真实框之间的距离。

针对Smooth L1没有考虑box四个坐标之间相关性的缺点：

图(a)中的L2损失值都是8.41，但是具有不同的IoU，图b中的L1损失值都是9.07，同样具有不同的IoU，可以得出，L1与L2的loss并不能衡量回归任务，不能等价于最后用于评测目标检测指标的IoU；

通过4个坐标来回归框并没有引入box四个顶点之间的相关性，IoU loss将4个坐标当作一个整体进行回归，IoU Loss的定义是先求出预测框和真实框之间的交集和并集之比，再求负对数，但是在实际使用中我们常常将IoU Loss写成1-IoU。如果两个框重合则交并比等于1，Loss为0说明重合度非常高，IoU满足非负性、同一性、对称性、三角不等性，相比于L1、L2等损失函数还具有尺度不变性，不论box的尺度大小，输出的IoU损失总是在0-1之间，所以能够较好的反映预测框与真实框的检测效果：

IoU loss定义如下，IoU Loss在设计损失时为规范化的坐标值/尺度建立了联系，可以直接反映预测框的检测效果，同时IoU对尺度也不敏感：

上图中的红色点表示目标检测网络结构中Head部分上的点（i,j），绿色的框表示Ground truth框, 蓝色的框表示Prediction的框，IoU loss的定义如上，先求出2个框的IoU，然后实际使用时IoU Loss =1-IoU；

伪代码如下：

其中，是预测Bounding box的面积，是真实Bounding box的面积，是两个区域的交集，是两个区域的并集，是对IOU的交叉熵损失函数；

 box位置的修正是通过对loss的反向传播迭代计算的。关于IOU Loss的反向传播具体推到过程可以移步到论文中，这里摘出结论部分如下：

 

从这个公式可以看出惩罚来自两个部分，预测框四个变量和预测框和真实框相交区域：

1 .损失函数和 成正比，因此预测的面积越大，损失越多； 

2 .同时损失函数和成反比，因此我们希望交集尽可能的大； 

根据求导公式为了减小IOU Loss，会尽可能增大相交面积同时预测更小的框。

缺点：
1、当loss=0时，如果两个框没有相交根据定义，此时不可导，不能反映两者之间的距离，可能距离很远。
2、当两者重合的时候，无法准确的反映两者的重合度大小，如下图所示。

IOU Loss虽然解决了Smooth L1系列变量相互独立和不具有尺度不变性的两大问题

但是它也存在两个问题：

1. 预测框和真实框不相交时（IoU(A,B)=0，此时损失函数不可导），不能反映出两个框的距离的远近。根据IOU定义loss等于0，没有梯度的回传无法进一步学习训练。
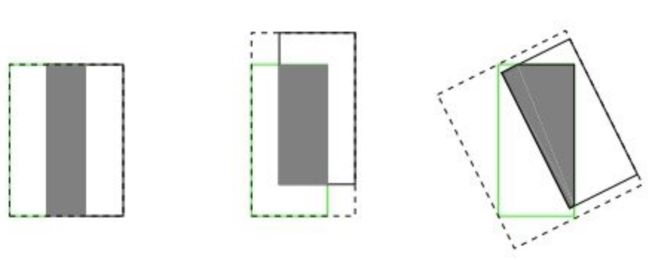
2. 预测框和真实框无法反映重合度大小。假设预测框和目标框的大小都确定，只要两个框的相交值是确定的，其IoU值是相同时，IoU值不能反映两个框是如何相交的。上图中三者具有相同的IOU，但是不能反映两个框是如何相交的，从直观上感觉第三种重合方式是最差的。

如上图所示，三种不同相对位置的框拥有相同的值IoU=0.33，但IoU值不能反映两个框是如何相交的，但直观上判断回归的效果是：左>中>右；

5. GIoU loss

上面指出IOU Loss的两大缺点：无法优化两个框不相交的情况；无法反映两个框如何相交的。

GIOU（Generalized Intersection over Union，）在2019年由斯坦福学者提出，考虑重叠面试，基于IOU解决了边框不相交时loss等于0的问题。
GIOU loss:先计算两个框的最小闭包面积，同时包括预测框和真实框的最小框面积，再计算出IOU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU。
 

《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression (CVPR2019)》

为解决上述IoU loss的问题，有学者提出了GIoU loss：

 

其中，是两个框之间的最小闭包框面积，即能同时包含两个框的最小框面积；

当时，表明两个框不重叠，且GIoU越小，两框的距离越远，时表明相距无穷远；

当时，表明两个框重叠，且GIoU越大，两框的重合程度越好，时表明完全重合；

GIoU取值范围为 [-1, 1]，在两框重合时取最大值1，在两框无限远的时候取最小值-1，同时与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度；

伪代码如下： 

其中C为包含A和B的外接矩形，用C减去A和B的并集除以C得到一个数值，然后再用框A和B的IoU减去这个数值即可得到GIoU的值；

GIoU采用距离度量损失函数，并且对尺度不敏感，依旧对具体的坐标值/尺度不敏感，上图中的GIoU(从左到右)：0.33，0.24，-0.1，其GIoU值同时反映了重叠方式。

缺点：
1、收敛速度很慢。
2、水平方向和垂直方向上这种情况，GIoU损失几乎退化为IoU损失。
3、当真实框完全被预测框包住（两框属于包含关系时）时，GIOU和IOU一样，如下图所示。

当真实框完全包裹预测框的时候，IoU和GIoU的值都一样，此时GIoU退化为IoU, 无法区分其相对位置关系，GIoU在考虑不重叠的情况时，只度量了距离却忽视了框的尺度：

GIoU Loss相同，但直觉上显然第三种情况回归更好；

由于GIOU仍然严重依赖IOU，因此在两个垂直方向，误差很大，基本很难收敛，这就是GIoU不稳定的原因。借用下图来说：红框内部分：C为两个框的最小外接矩形，此部分表征除去两个框的其余面积，预测框和真实框在相同距离的情况下，水平垂直方向时，此部分面积最小，对loss的贡献也就越小，从而导致在垂直水平方向上回归效果较差。

6. DIoU Loss

DIOU（Distance-IoU，距离），在2020年提出，考虑重叠面积和中心点距离，基于IOU解决了CIOU收敛慢的问题。
DIOU Loss：将目标与anchor之间的距离，重叠率以及尺度都考虑进去，其中代表的是计算两个中心点间的欧式距离。 代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。
 

论文地址：

《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (AAAI2020)》

针对上述GIoU的问题，（即预测框和真实框是包含关系的情况或者处于水平/垂直方向上，GIOU损失几乎已退化为IOU损失，即 |C−A∪B|→0 ,导致收敛较慢），有学者将GIOU中引入最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程；

 

 

其中，绿色框为真实框，黑色框为预测框，灰色框为两者的最小外界矩形框，b和分别是预测框和真实框的中心点，度量了两点之间的欧式距离，c是预测框和真实框的最小闭包框的对角线距离；

【当目标框包裹时，因为加入了位置信息，DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。
对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失】

DIoU跟GIoU一样，能在两框不重叠时为训练提供方向，DIoU在两框不重叠时既考虑了距离，也考虑了尺度，在两框处于水平或垂直方向上时，DIoU依旧能为训练网络做出不错的贡献，DIoU直接最小化两框的距离，拥有更加平滑的损失曲面，因此收敛比GIoU更快；

7. CIoU Loss

CIoU（Complete-IoU，）考虑重叠面积、中心点距离、纵横比，基于DIOU提升回归精度问题。
CIOU Loss：考虑到bbox回归三要素中的长宽比还没被考虑到计算中，因此，进一步在DIoU的基础上提出了CIoU，加入了一个惩罚影响因子，这个因子把预测框长宽比拟合目标框的长宽比考虑进去。
论文地址：

《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (AAAI2020)》

在DIoU Loss的基础上，论文继续引入长宽比（纵横比）的惩罚得到CIoU Loss。CIOU的惩罚项是在DIOU的惩罚项基础上加了一个影响因子 ，这个因子把预测框纵横比拟合真实框的纵横比考虑进去。惩罚项公式如下：

其中是用于做trade-off的参数：

v是用来衡量长宽比一致性的参数，，完全相等时v=0：

完整的CIoU损失函数：

 

然而在CIoU的定义中，衡量长宽比过于复杂，从以下两个方面减缓了收敛速度：

长宽比不能取代单独的长宽，比如、都会导致v=0；

 从v的导数可以得到，说明和在优化时意义相反；

YOLOv4的location_loss使用了ciou。ciou在iou的基础上考虑了边框的重合度、中心距离和宽高比的尺度信息。

 8. EIoU Loss
CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。针对这一问题，有学者在CIOU的基础上将纵横比拆开，提出了EIOU Loss，并且加入Focal聚焦优质的锚框，该方法出自于2021年的一篇文章。

论文地址：

《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》

解决CIoU定义中的不足，引入了解决样本不平衡问题的Focal Loss思想，将CIoU的取代为

EIoU Loss的定义为：

EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIOU中的方法，但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小，使得收敛速度更快。惩罚项公式如下：

其中 Cw 和 Ch 是覆盖两个Box的最小外接框的宽度和高度。

考虑到BBox的回归中也存在训练样本不平衡的问题，即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本，质量较差的样本会产生过大的梯度影响训练过程。作者在EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss，梯度的角度出发，把高质量的锚框和低质量的锚框分开，惩罚项公式如下：

其中 Cw 和 Ch 是覆盖两个Box的最小外接框的宽度和高度。

考虑到BBox的回归中也存在训练样本不平衡的问题，即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本，质量较差的样本会产生过大的梯度影响训练过程。作者在EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss，梯度的角度出发，把高质量的锚框和低质量的锚框分开，惩罚项公式如下：

其中IOU = |A∩B|/|A∪B|， 为控制异常值抑制程度的参数。该损失中的Focal与传统的Focal Loss有一定的区别，传统的Focal Loss针对越困难的样本损失越大，起到的是困难样本挖掘的作用；而根据上述公式：IOU越高的损失越大，相当于加权作用，给越好的回归目标一个越大的损失，有助于提高回归精度。

9. IoU loss
论文地址：

《Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression》

将现有的基于IoU的Loss推广到一个新的PowerIoU系列的Loss，它具有一个幂次IoU项和一个附加的幂次正则项，可以显著的超过现有的基于IoU的损失，通过调节α，使探测器更灵活地实现不同水平的bbox回归精度，对小数据集和噪声的鲁棒性更强；

并且通过实验发现，在大多数情况下，取α=3的效果最好。 

10. SIoU loss
论文地址：

《SIoU Loss: More Powerful Learning for Bounding Box Regression》

好的目标框回归损失应该考虑三个重要的几何因素：重叠面积，中心点距离，长宽比；还应该考虑真实框与期望框不匹配的方向，所以提出了一个新的损失函数SIoU，其中惩罚度量被重新定义考虑中心点向量之间的期望角度回归；

SIoU损失函数由4个cost函数组成：

将角度成本贡献转化为损失函数，收敛的过程首先尽量最小化 if， ， others：

10.1 Angle cost

添加这种角度感知损失函数（LF） 组件背后的想法是最大限度地减少与距离相关的“奇妙”中的变量数量。基本上，模型将尝试首先将预测带到 X 或 Y 轴（以最接近者为准），然后沿着相关轴继续接近。

 Angle cost的曲线如图2所示：

10.2 Distance cost

考虑到上面定义的Angle cost，重新定义了Distance cost：

10.3 Shape cost

Shape cost(形状cost)的定义为：

的值定义了每个数据集的Shape cost及其值是唯一的。 的值是这个等式中非常重要的一项，它控制着对Shape cost的关注程度。如果 的值设置为 1，它将立即优化一个Shape，从而损害Shape的自由移动。为了计算 的值，作者将遗传算法用于每个数据集，实验上 的值接近 4，文中作者为此参数定义的范围是 2 到 6。

 

10.4 IoU Cost

IoU cost的定义为：

其中，

10.5 SIoU Loss

loss function：

随后，我将基于YOLO系列给出的损失函数作为实例，因为它包括了多数情况。
YOLO系列的损失包括三个部分: 回归框loss, 置信度loss, 分类loss.

从最重要的部分开始: 回归框loss.
        从 v1 to v3, 回归框loss更像是MSE，v1是(x-x’)^2 + (y-y’)^2，而对w和h分别取平方根做差，再求平方，用以消除一些物体大小不均带来的不利。
        v2和v3则利用(2 - w * h)[(x-x’)^2 + (y-y’)^2 + (w-w’)^2 + (h-h’)^2], 将框大小的影响放在前面作为系数，连x和y部分也一块考虑了进去。
        v4作者认为v1-v3建立的类MSE损失是不合理的。因为MSE的四者是需要解耦独⽴的，但实际上这四者并不独⽴，应该需要⼀个损失函数能捕捉到它们之间的相互关系。因此引入了IOU系列。经过其验证，GIOU，DIOU, CIOU，最终作者发现CIOU效果最好。注意，使用的时候是他们的loss，应该是1-IOUs，因为IOU越大表示重合越好，而loss是越小越好，因此前面加1-，令其和平常使用规则一致。
        v5作者采用了GIOU，具体还需要等他论文出现。

IOU, A与B交集 / A与B并集，在这一般是ground truth和predict box之间的相交面积/他们的并面积

 置信度损失和分类Loss.
这里先给出v1-v3的损失函数，可以看出，v1-v2中置信度误差和分类误差均使用的是MSE；

从v2到v3, 不同的地⽅在于，对于类别和置信度的损失使⽤交叉熵。

 

 

 v4在v3的基础上对回归框进行的loss回归预测，就是基于CIOU的回归函数

边界框回归的三大几何因素：重叠面积、中心点距离、纵横比

• IOU Loss：考虑了重叠面积，归一化坐标尺度；
• GIOU Loss：考虑了重叠面积，基于IOU解决边界框不相交时loss等于0的问题；
• DIOU Loss：考虑了重叠面积和中心点距离，基于IOU解决GIOU收敛慢的问题；
• CIOU Loss：考虑了重叠面积、中心点距离、纵横比，基于DIOU提升回归精确度；
• EIOU Loss：考虑了重叠面积，中心点距离、长宽边长真实差，基于CIOU解决了纵横比的模糊定义，并添加Focal Loss解决BBox回归中的样本不平衡问题。

	IOU Loss	GIOU Loss	DIOU Loss	CIOU Loss
优点	IOU算法是目标检测中最常用的指标，具有尺度不变性，满足非负性；同一性；对称性；三角不等性等特点。	GIOU在基于IOU特性的基础上引入最小外接框解决检测框和真实框没有重叠时loss等于0问题。	DIOU在基于IOU特性的基础上考虑到GIOU的缺点，直接回归两个框中心点的欧式距离，加速收敛。	CIOU就是在DIOU的基础上增加了检测框尺度的loss，增加了长和宽的loss，这样预测框就会更加的符合真实框。	EIOU在CIOU的基础上分别计算宽高的差异值取代了纵横比，同时引入Focal Loss解决难易样本不平衡的问题。
缺点	1.如果两个框不相交，不能反映两个框距离远近 2.无法精确的反映两个框的重合度大小	1.当检测框和真实框出现包含现象的时候GIOU退化成IOU 2.两个框相交时，在水平和垂直方向上收敛慢	回归过程中未考虑Bounding box的纵横比，精确度上尚有进一步提升的空间	1. 纵横比描述的是相对值，存在一定的模糊 2. 未考虑难易样本的平衡问题	待定

参考：
代码实现

Python代码

细数目标检测中的损失函数

目标检测回归损失函数总结_胖虎

遵循CC 4.0 BY-SA版权协议，转载

仅为学习记录，侵删！
————————————————

原文链接：https://blog.csdn.net/senbinyu/article/details/108310976

五、目标检测：损失函数的设计和改进 - 知乎 (zhihu.com)

原文链接：https://blog.csdn.net/panghuzhenbang/article/details/125276230

原文链接：https://blog.csdn.net/threestooegs/article/details/122594287