2022年数维杯数学建模B题 大规模新型冠状病毒疫情最优应对策略研究求解全过程文档及程序

2022年数维杯数学建模

A题 大规模新型冠状病毒疫情最优应对策略研究

原题再现：

  无论是 2022 年 3 月初在吉林省长春市大规模爆发的新型冠状病毒疫情（COVID-19），还是 4 月初在上海及 5 月初在北京大规模爆发的疫情，均显示出了一些普遍存在的难点问题。考虑到近期或未来仍然有部分省份存在潜在的大规模爆发风险，因此非常有必要引进更为科学的 COVID-19 应对策略，并努力为有效降低大规模疫情防控成本、缩短疫情防控周期及保障各省经济的稳定可持续发展方面提供可靠的依据。
  在 COVID-19 疫情应对方面所面临的主要问题包括疫情大规模爆发期间医疗资源的合理分配与调度问题、科学核算监测方案的制定问题、居民基本生活物资的保障问题及后期的复工复产方案设计等问题。
  请大家结合数学建模的方法，解决如下的五个问题：
  1、试分析长春市、上海市及北京市疫情传播的基本规律及其关键性因素，并预测出上海疫情和北京疫情预计社会面清零的时间节点；
  2、在疫情爆发期间医疗资源的合理分配与调度是至关重要的，你能否提出充分考虑不同区域人口、面积与经济发展水平的医疗物资的合理指派方案，同时在此方案中你需要充分考虑因未能得到及时治疗所导致的非确诊病例的伤亡损失；
  3、在疫情爆发期间合理的核酸检测方案的设计是至关重要的，某大型小区具有 103 栋楼，封闭人数 18326 人。其中最高 6 层、3 个单元、36 户及平均入住率 70%的楼 60 栋，最高 11 层、2 个单元、44 户及平均入住率 75%的楼 20 栋，最高 18 层、3 个单元、126 户及平均入住率 80%的楼 23 栋。你能否结合上述数据提供考虑不同类型楼栋特征的最优核算监测分组方案、时间间隔及其具体的时间节点？
  4、在疫情管控期间居民生活物资的订购与发放也同样非常关键，在基本生活物资供给有限的情况下你能否提供一个更为科学的生活物资订购与指派方案？在模型中请你需要明确考虑因生活物资交互而产生的疫情传播风险。
  5、在疫情得到有效的控制情况下，逐步的复工复产方案的设计也是非常有必要的。你能否提供考虑不同行业和每日新增确诊人数的复工复产计划？

整体求解过程概述(摘要)

  当前大规模爆发的新型冠状病毒疫情可以看出我国疫情防控仍普遍存在的一些难点问题，同时考虑到近期或未来仍有部分省份存在潜在的大规模疫情爆发风险。本文通过建立 Gaussian-SIRD 模型、SEIAPHR 模型及生活物资订购与分配模型，以解决当前COVID-19 在疫情应对方面所主要面临的五个问题。
  针对问题一，首先，基于三市疫情情况总结传播基本规律为传播力强与隐匿性强，现阶段处于流行高峰、流行奥密克戎变异株、开学复工以及思想松懈是关键性因素。其次，建立 SIRD 模型与 Gaussian-SIRD 模型，利用 Matlab 进行求解。最后，进行综合分析可预测上海在 2022 年 5 月 24 日至 5 月 30 日期间实现确诊病例零新增，北京疫情预计在 5 月 20 日左右就会陆续解封恢复正常。
  针对问题二，首先，本文基于 SEIR 模型增加无症状感染者 A、确诊并治疗 H 等参数建立 SEIAPHR 模型。其次，以上海 16 个行政区 127 个发热门诊为例，结合多个场景对各行政区医疗资源日需求量进行评估，根据上海市卫生系统最大承载力与医疗物资最大生产力得出初步分配方案。最后，在最低非确诊病例死亡损失比的前提下，对分配方案进行二次优化，得出上海市各行政区每日医疗资源分配方案。
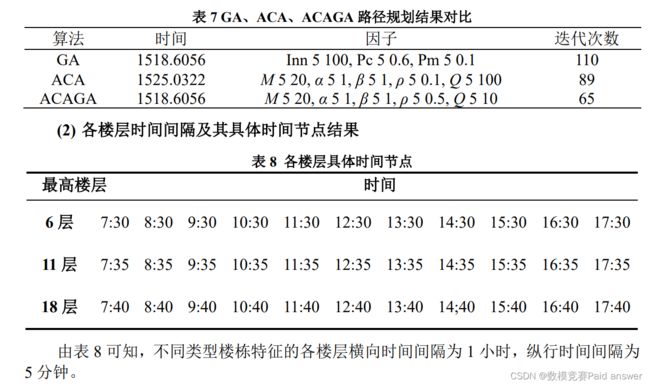
  针对问题三，首先，基于已知数据分析确定核酸检测位点定为 20 个，记最高 6 层的楼型为 A，最高 11 层的楼型为 B，最高 18 层的楼型为 C。其次，以检测时间最短，路径最短为目标，运用多目标混合遗传算法 -蚁群优化算法的任务分配技术，得出最佳的核酸检测位点坐标为 (310,40)。最后，利用MATLAB 计算出最优核酸检测分组方案为每隔 30 分钟对 A 型楼层住户单独检测，每组 135 人，具体的时间节点及最终核酸检测分组策略见表 9 所示。
  针对问题四，首先，建立了生活物资订购模型，将生活物资根据 ABC 分类法进行分类，得出重要性生活物资、稀缺性生活物资、时效性生活物资。其次，对三类物资分别建立模型，最终得出重要性生活物资的订购方案为：公式(5-44)，稀缺性生活物资的订购方案为：公式(5-45)，时效性生活物资的订购方案为：公式(5-46)。最后，考虑到生活物资的交互次数与运输时间对疫情传播的影响，建立了三方应急生活物资指派模型，将交互次数与运输时间设为约束条件，求得指派方案为∑=,其中<=，且满足∑最小。
  针对问题五，基于国务院颁发的复工复产相关政策，根据不同地区实际情况提出不同行业和每日新增确诊人数复工复产计划。首先，每日新增确诊在 0-15 人之间的河南地区，提出制造业企业分区、分级复工，实现闭环管理，建造智能车间复工等计划。其次，每日新增确诊在 15-30 人的北京地区，餐饮业分别实施菜品调整、外卖消毒配送等复工计划。最后，每日新增确诊在 300 人以上的上海地区，物流业制定创新经营复工、减少批次等计划。有效降低在传递生活必需品等物资时产生的交叉感染风险，为打赢实现疫情动态化、常态化全面清零政策战役做足充分准备。

问题分析：

  针对问题一，首先，收集三市疫情传播速度等相关信息，计算无症状感染者比例等数据，总结疫情传播基本规律与关键性因素。其次，收集全部感染病例、每日住院病例、累计康复病例以及死亡病例等数据，建立 SIRD 模型与 Gaussian-SIRD 模型，计算疫情传染率，预测人口规模和感染高峰日方面的敏感性。最后，根据预测确诊人数确定社会清零时间节点。
  针对问题二，为探究各地区在不同场景下的最优医疗资源配给方案。以上海市为例，将上海市各行政区地区、人口与面积进行统筹分析，计算各行政区医疗资源日最大需求量。以最低非确诊病例死亡损失比为前提，对配给方案进行优化得到最优方案。
  针对问题三，首先基于已知数据与收集到的北京市某小区居民规模数据分析确定出该小区内不同类型楼栋的核酸检测位点定，标记不同层高的楼型。其次以检测时间最短，路径最短为目标，运用一种基于多目标混合遗传算法-蚁群优化算法的任务分配技术，基于响应时间、完成时间和吞吐量得出最佳的核酸检测位点坐标。最后，结合不同类型楼栋特征，利用 MATLAB 进行算法迭代计算出最优核酸检测分组方案，得出不同类型楼层每组检测人数和检测时间节点。
  对于问题四，本文需要解决的问题是在疫情管控期间制定一个科学的生活物资订购与指派方案，首先对生活物资的订购模型进行建立，对于应急事件，疫情下的生活物资种类繁多，数量巨大，对于库存物资的管理与控制有非常大的要求，这时常用到的控制分类方法为 ABC 分类法，将生活物资分为三种不同类。然后对三种不同类型的物资分别建模，得到订购方案。最后考虑到生活物资的交互次数与运输时间对疫情传播的影响，将交互次数与运输时间设为约束条件，建立三方应急生活物资指派模型，求出指派方案。
  针对问题五，首先，由于行业和每日新增确诊人数的不同，对各地区各行业复工复产的计划存在较大差异，本文选取代表性地区进行制定复工复产计划。其次，将新增确诊人数划分为三个等级，针对各个等级制定不同程度的防疫措施。最后，本文选取制造业、餐饮业、物流业，结合各个行业特征提出具体措施。

模型假设：

模型的建立与求解

疫情传播基本规律与关键性因素分析

  (1)疫情传播基本规律
  一是传播力强：国内外的研究表明，奥密克戎变异株的传播力要大于流感和此前的新冠病毒的其他变异株。如果在没有防护措施的情况下，一个人平均可以传播 9.5 个人，在上海市的一些人口密度大、人员容易密集的劳动作业场所所发生的聚集性疫情中，就呈现出这一典型的特征。
  二是隐匿性强：在上海市疫情中，无症状感染者比例达到 90%左右，以近 10 天公布的数据为例，高的有 93%，低的也有 85%；而即便是有症状的病例，其症状也相对较轻，主要是流鼻涕、打喷嚏、喉咙痛等，患者往往会误以为这是普通感冒或者是季节性流感，导致未及时就医，这也会使得在疫情的早期，医疗机构能够及时发现的病例数大幅减少，甚至是较长时间后才会发现疫情，即容易造成隐匿性传播。归纳起来，正是由于奥密克戎变异株自身的特点，所以在本轮疫情的早期，等我们发现阳性感染者的时候，疫情其实已经在一定范围内发生了隐匿性传播，然后又进一步通过批发市场、菜市场、集体单位等人群聚集场所快速扩散，直至在较短时间内进一步引发了社区的广泛传播，从而导致目前的疫情状况。
  (2)关键性因素
  主要的原因有 4 个方面：
  一是从 2021 年 12 月开始，全球新冠肺炎进入了第四波的流行高峰，现在已经连续11 周，每周报告的病例数都超过了 1000 万，目前仍然是处于高位流行的水平。特别是今年以来，我们周边的国家和地区疫情快速上升，与我国疫情水平的“压力差”不断增大。今年 1-2 月，每天输入的感染者数日均是 91 例，远高于 2020 年的 22 例和 2021 年的 32 例。今年 3 月以来，日均输入感染者数超过 200 例，单日最高能超过 300 例。可以说，近期疫情输入的压力明显增加。
  二是近期全球主要流行的奥密克戎变异株，特别是 BA.2 亚分支，较以往病毒株的传播性和隐匿性都更强，早期发现难度确实更大了，导致疫情发现时往往已经波及了一定的范围，可以说疫情处置、控制的难度也更加大了。
  三是今年2月下旬恰逢我国春节假期结束，学生春季学期开学，企业工人复工等等，带来了人员的大规模流动，加之会议培训、婚丧嫁娶等各类人员聚集性的活动增加，可以说成为了疫情的“传播器”和“放大器”，导致疫情迅速扩散，甚至是跨区域的传播。四是有的地方认为奥密克戎变异株症状轻，流感化，思想松懈麻痹，有“歇歇脚、缓一缓”的心态，各方面准备不足，常态化防控和应急处置放松了要求。

SIRD 模型与 Gaussian-SIRD 模型的建立

  疫情反复，预测方法应该同时拟合尽可能多的数据，以进行有效的预测。在对疫情趋势进行预测时数据量普遍较大，其中包括全部感染病例、每日住院病例、累计康复病例以及死亡病例等，因此需考虑预测方法对数据量的精度和敏感性。在这些方面，我们对标准 SIRD 模型进行了评价，观察到 SIRD 模型具有快速抓取 COVID-19 主要发展趋势的能力。
  但由于 SIRD 模型在对暴露人群规模的预测不是很准确，而 Gaussian-SIRD 模型则在此方面具有一定优势，能提供较长时期内的精确预测，因此考虑建立 Gaussian-SIRD模型，结合上述建立的 SIRD 模型，综合两种不同数据处理方法进行预测。

SIRD 模型与 Gaussian-SIRD 模型的求解

  利用 Matlab 对 SIRD 模型记忆 Gaussian-SIRD 模型求解，以上海 3 月 10 日之后 20天、40 天、50 天的 COVID-19 数据，研究 SIRD 和高斯-SIRD 模型在预测人口规模和感染高峰日方面的敏感性，图 1 给出了优化的 SIRD 和高斯-SIRD 模型的结果，并对易感群体、感染群体、康复群体和死亡群体进行了比较。

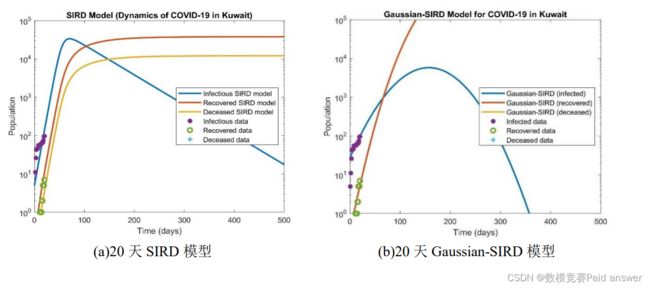
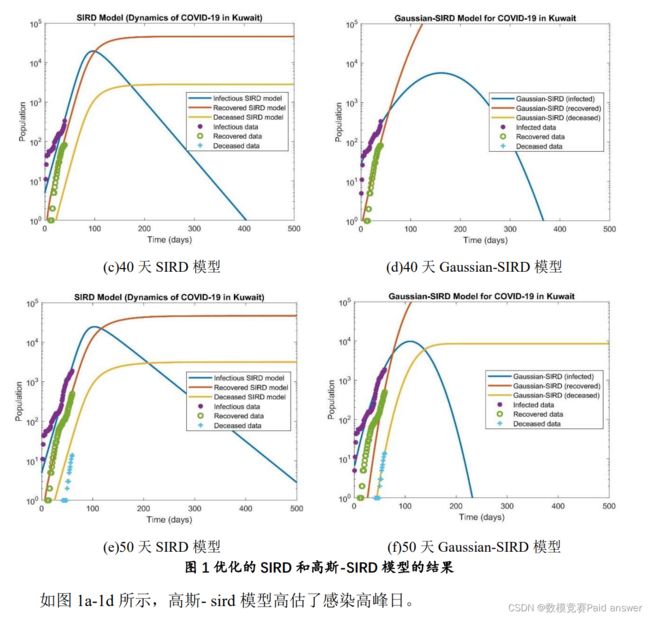
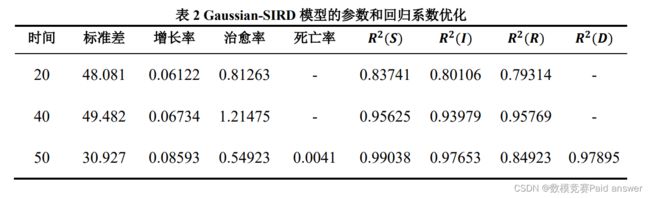
  上海市预测结果
  使用上海市 4 月 27 日预测的本轮疫情感染数值和 5 月 4 日、5 日、6 日的实际新型冠状病毒确诊人数，在基于 4 月 27 日预测上海市新型冠状病毒确诊人数的基础上，通过建立的 SIRD 模型与 Gaussian-SIRD 模型，利用 Matlab 进行求解，进行综合分析可预测在 2022 年 5 月 24 日至 5 月 30 日期间实现确诊病例零新增。
  北京市预测结果
  同理可得，北京疫情预计在 5 月 20 日左右就会陆续解封恢复正常，但具体还要看后续疫情新增情况。若是北京在五月十几号能实现社会面清零，到月底就能差不多陆续恢复正常。若是在 5 月 20 日之后社会面还有零散新增，那预计到六月份左右才能恢复正常。而北京居民生活恢复正常，是按照“三区”划分相关要求，逐步、分批有序开放社会面人员流动和生产生活，直至完全恢复常态。

SEIAPHR 模型的建立

  基于新冠病毒流行的不同状态与传播机理，在SEI仓库模型基础上，增加确诊患者，形成“易感染-潜性感染-传染者-住院/隔离者-移除者”5 个仓储，将隔离 14 天无症状的感染者同时引入各仓储，构建 SEIHAPHR 模型。首先，采用作业成本法统筹计算各地区人口、面积以及各医疗机构各项医疗服务所需要的时间1，统计各地区直接医疗成本2（诊断检测费、健康检测费、药物治疗费用、治疗相关费用与住院费用）。

SEIAPHR 模型的求解

将数据中的异常值进行剔除后得到各地区数据如表 3 所示的上海各地区数据表。

  从上海市全市来观察，将上海市分为城市中心区与城郊区，发热门诊分布如下。结合上海市各行政区不同医疗设施与地区状况分析，整合疫情发生的预期风险要素，并将不同状况下疫情发生过程、防控策略纳入模型参考因素，得到如下表 4 场景因素。

  由上表计算并对各地区消耗资源进行预估，并通过优化函数进行二次计算优化预估。根据抗击新冠疫情现状实际需求，结合新冠疫情得发现、追踪、检测、诊断等多个防控流程，将医疗资源分为三类：临床治疗、实验室分析检测使用、流行病学防控。临床治疗医疗资源包括临床执业医师、护士、护工、普通病床、隔离病床、ICU 病床、呼吸机、吸氧设备。实验室分析检测医疗资源包括：核算检测采样人员、核算采样保障人员、检测设备、个人防护物资等。
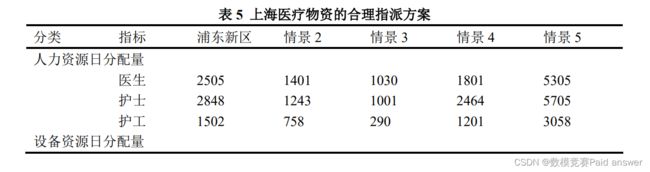
  流调防控资源包括消杀人员、社区防空人员、社区志愿者以及个人防护用品消耗等。卫生资源的供需平衡与医疗卫生系统的最大承载力相关，患者病例大于最大承载力则会导致部分患者得不到及时有效的治疗，进而出现死亡率上升等事件。将优化后的情景进行比较同时参考上海市各资源每日最大生产量得到结果如表 5 所示。

数据整理与分析

  将问题中的所给数据进行整理，得到如表 6 所示的某大型小区不同类型楼栋特征信息表。

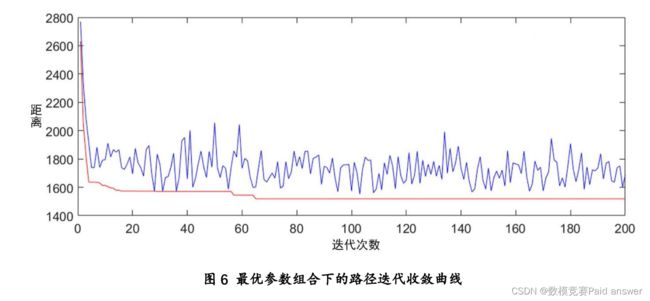
  样本的时间顺序安排以确保每轮时间最短。本文提出了一种基于多目标混合遗传算法-蚁群优化算法(HGA-ACO)的任务分配技术。算法将遗传算法和蚁群优化算法结合在一起，利用遗传算法初始化蚁群优化的有效信息素。提出的路径规划与调度模型可为提高医院物流效率提供可靠的参考。本研究在算法的早期使用蚁群算法来获得最佳路径作为良好的父代，然后在后期使用 GA 融合将 GA 的启发式遗传信息添加到蚁群算法中。首先，通过ACA 的每次迭代得到最优解，并将其视为精英个体。精英群体由多个精英个体组成，作为遗传算法的初始种群。这样，遗传算法就有了一个高质量的解空间，其效率和精度可以大大提高。然后，遗传算法通过复制、交叉和变异过程生成的较好解更新了蚁群算法中的较差解，并以此作为当前的最优路径更新蚁群算法，有效地避免了蚁群算法陷入局部最优。实验结果表明，该框架在任务分配和服务质量参数保证方面具有较好的性能。

遗传算法-蚁群优化算法

遗传算法-蚁群优化算法的求解

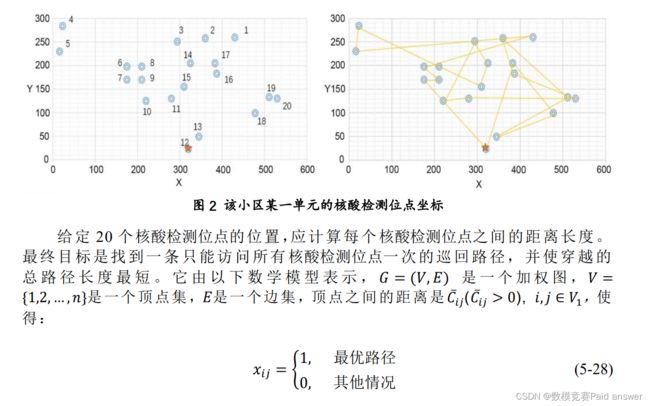
  根据实际距离，在该小区的西南角选择一个原点，以建立二维坐标系，并通过该小区的俯视图标记支持人员需要到达的点的实际位置。对于一些占地面积较大的建筑，选择每栋建筑的入口作为计算的收集点。如果一个单元包含多个点，则应根据注释选择具体坐标，每层楼的每户人家都需要自行下楼到核酸检测点，可采取重复路径到核算检测点收集样本，每个核酸检测点的最长路径只允许同一时间段覆盖一个单元，不允许重复（循环移位）。假设每两点都可以通过一条直线到达，如图 2 该小区某一单元的核酸检测位点坐标所示。在实际场景的路径中必须有一条虚线，一单元内不同楼配备的核算检测点及路径如图 3 所示。但是，整个小区区域的规模不是很大，折线距离和近似直线距离以及时间之间几乎没有差异。

生活物资订购与指派模型的建立

  ABC 分类法作为常用的控制分类方法，主要对生活物资的占用资金比例与占用仓库总数目的比例来划分为三个不同类别，分别为特别重要的库存（A 类库存）、一般重要的库存（B 类库存）和不重要的库存（C 类库存）根据三类物资的不同特点，分别采取重点、次要和一般三种不同程序的管理，以达到最经济和最有效地使用物资的目的。其中三个分类等级及占比如表 10 所示。

  在疫情发生期间，生活物资的具体特征会对物资的库存模式和储备方案产生影响，因此需要针对疫情对生活物资进行符合应急事件需求的分类管理。对于不同属性的生活物资在库存管理和控制上采取不同的策略。将生活物资这三个方面的属性作为基础，对单一物资的应急属性特征建立如表 11 所示的生活物资分类体系。


  本文从中选取十种应急物资为例进行说明 。采用以上的评价标准对上面的每一种生活物资进行量化评价，可以对不同的生活物资进行分类，分类结果如表 12 所示。

  采用 ABC 分类法的思想对疫情管控期间所需的生活物资进行分类，将其按照应急物资的作用和用途分为重要性、稀缺性和时效性，在库存管理工作中使用不同订购模型实现区别化管理，有利于发挥不同属性生活物资在应急事件中的作用。

重要性生活物资订购模型的建立

  对于重要性生活物资，需要一定的库存数量，实际的情况中，库存数量、占用资金一集存储空间是相互制约的，因此可以采用存储地有限的经济订购模型。由于仓库存储空间有限，因此考虑在确定不同类型物资的最优库存时，还需要考虑存储场地的制约。

稀缺性生活物资订购模型的建立

  对于稀缺性生活物资，其主要的特点为难以实现大量的筹备，市场此时的存储量较少以及生产的效率较低，当疫情爆发时，这类物资往往变得难以获取，采购、调运困难，供货能力较弱以及难以囤积大量此类物资导致库存的缺失率较高。鉴于这类物资的特点，在稀缺类的库存策略方面要认真考虑其特殊属性，在库存管理策略上采取保持一定的库存的战略，适当的增加安全库存的数量，建立科学的管理模型，尽力降低该类物资的缺货成本，充分发挥其作用。
  定期订货法的基本原理是按照预先明确的订货时间间隔按时间周期进行订货以补充库存的库存控制方法，定期订货发是基于时间控制的订货方式。实际生活中，定期订货需要设定相应的订货周期和最高库存量来达到控制合理的库存量的目的，在定期订货法的具体应用中，只需要设置合理的订货间隔和最高库存量，就能够实现保障需求和节省库存成本的目的，图 8 给出了定期订货法的原理模型：

  定期订货法的原理描述中需要按照固定间隔期进行订货，其缺点在于没有充分考虑到库存水平 IIP 的实际情况，也就是说不论库存水平下降多少（甚至库存消耗极小而无须订货）都要按时间周期发出订货要求。因此对定期订货法进行修正，修正后的定期订货法称为最大最小定期订货法，其原理图如图 9 所示：

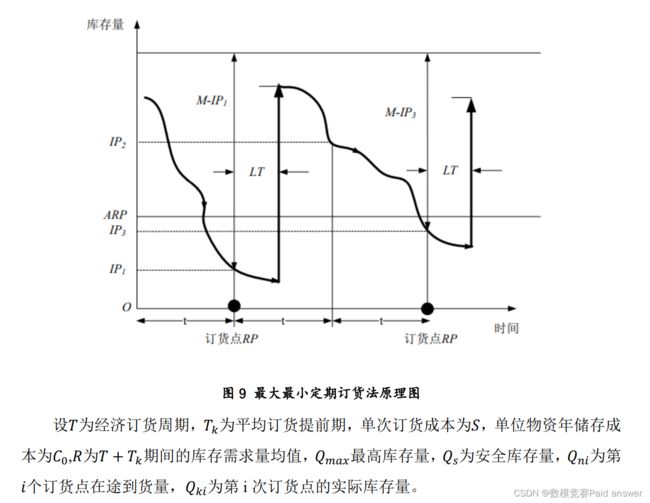
重要性生活物资订购模型求解

稀缺性生活物资订购模型求解

生活物资指派模型求解

论文缩略图：

程序代码：

matlab程序：

citys=[[1304,2312];[3639,1315];[4177,2244];[3712,1399];[3488,1535];[3326,1556];[3238,12
29];[4196,1004];[4312,790];[4386,570];[3007,1970];[2562,1756];[2788,1491];[2381,1676];[
1332,695];[3715,1678];[3918,2179];[4061,2370];[3780,2212];[3676,2578];[4029,2838];[426
3,2931];[3429,1908];[3507,2367];[3394,2643];[3439,3201];[2935,3240];[3140,3550];[2545,2
357];[2778,2826];[2370,2975]];
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
 for j = 1:n
 if i ~= j
 D(i,j) = sqrt(((citys(i,1) - citys(j,1))^2)+((citys(i,2) - citys(j,2))^2));
 else
 D(i,j) = 0;
 end
 end
end
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数（信息素释放量）
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
while iter <= iter_max
 % 随机产生各个蚂蚁的起点城市
 start = zeros(m,1);
 for i = 1:m
 temp = randperm(n);
 start(i) = temp(1);
 end
 Table(:,1) = start;
 % 构建解空间
 citys_index = 1:n;
 % 逐个蚂蚁路径选择
 for i = 1:m
 % 逐个城市路径选择
 for j = 2:n
 tabu = Table(i,1:(j - 1))； % 已访问的城市集合
 allow_index = ~ismember(citys_index,tabu);
 allow = citys_index(allow_index);% 待访问的城市集合
 P = allow;
 % 计算城市间转移概率
 for k = 1:length(allow)
 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
 end
 P = P/sum(P);
  % 轮盘赌法选择下一个访问城市
 Pc = cumsum(P);
 target_index = find(Pc >= rand);
 target = allow(target_index(1));
 Table(i,j) = target;
 end
 end
 % 计算各个蚂蚁的路径距离
 Length = zeros(m,1);
 for i = 1:m
 Route = Table(i,:);
 for j = 1:(n - 1)
 Length(i) = Length(i) + D(Route(j),Route(j + 1));
 end
 Length(i) = Length(i) + D(Route(n),Route(1));
 end
 % 计算最短路径距离及平均距离
 if iter == 1
 [min_Length,min_index] = min(Length);
 Length_best(iter) = min_Length;
 Length_ave(iter) = mean(Length);
 Route_best(iter,:) = Table(min_index,:);
 else
 [min_Length,min_index] = min(Length);
 Length_best(iter) = min(Length_best(iter - 1),min_Length);
 Length_ave(iter) = mean(Length);
 if Length_best(iter) == min_Length
 Route_best(iter,:) = Table(min_index,:);
 else
 Route_best(iter,:) = Route_best((iter-1),:);
 end
 end
 % 更新信息素
 Delta_Tau = zeros(n,n);
 % 逐个蚂蚁计算
 for i = 1:m
 % 逐个城市计算
 for j = 1:(n - 1)
 Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + 
Q/Length(i);
 end
 Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + 
Q/Length(i);
 end
  Tau = (1-rho) * Tau + Delta_Tau;
 % 迭代次数加 1，清空路径记录表
 iter = iter + 1;
 Table = zeros(m,n);
end
 tabu = Table(i,1:(j - 1))% 已访问的城市集合
 ↑
错误: 输入字符不是 MATLAB 语句或表达式中的有效字符。
while iter <= iter_max
 % 随机产生各个蚂蚁的起点城市
 start = zeros(m,1);
 for i = 1:m
 temp = randperm(n);
 start(i) = temp(1);
 end
 Table(:,1) = start;
 % 构建解空间
 citys_index = 1:n;
 % 逐个蚂蚁路径选择
 for i = 1:m
 % 逐个城市路径选择
 for j = 2:n
 tabu = Table(i,1:(j - 1)); % 已访问的城市集合
 allow_index = ~ismember(citys_index,tabu);
 allow = citys_index(allow_index);% 待访问的城市集合
 P = allow;
 % 计算城市间转移概率
 for k = 1:length(allow)
 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
 end
 P = P/sum(P);
 % 轮盘赌法选择下一个访问城市
 Pc = cumsum(P);
 target_index = find(Pc >= rand);
 target = allow(target_index(1));
 Table(i,j) = target;
 end
 end
 % 计算各个蚂蚁的路径距离
 Length = zeros(m,1);
 for i = 1:m
 Route = Table(i,:);
 for j = 1:(n - 1)
 Length(i) = Length(i) + D(Route(j),Route(j + 1));
 end
 Length(i) = Length(i) + D(Route(n),Route(1));
 end
 % 计算最短路径距离及平均距离
 if iter == 1
 [min_Length,min_index] = min(Length);
 Length_best(iter) = min_Length;
 Length_ave(iter) = mean(Length);
 Route_best(iter,:) = Table(min_index,:);
 else
 [min_Length,min_index] = min(Length);
 Length_best(iter) = min(Length_best(iter - 1),min_Length);
 Length_ave(iter) = mean(Length);
 if Length_best(iter) == min_Length
 Route_best(iter,:) = Table(min_index,:);
 else
 Route_best(iter,:) = Route_best((iter-1),:);
 end
 end
 % 更新信息素
 Delta_Tau = zeros(n,n);
 % 逐个蚂蚁计算
 for i = 1:m
 % 逐个城市计算
 for j = 1:(n - 1)
 Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + 
Q/Length(i);
 end
 Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + 
Q/Length(i);
 end
 Tau = (1-rho) * Tau + Delta_Tau;
 % 迭代次数加 1，清空路径记录表
 iter = iter + 1;
 Table = zeros(m,n);
end
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
最短距离:15828.7082
最短路径:15 14 12 13 11 23 16 4 2 5 6 7 8 9 10 3 18 
17 19 24 25 20 21 22 26 28 27 30 31 29 1 15
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
 [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
 text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

绘图程序：

function createfigure(cdata1)
%CREATEFIGURE(CDATA1)
% CDATA1: image cdata
% 由 MATLAB 于 08-May-2022 17:17:55 自动生成
% 创建 figure
figure1 = figure;
% 创建 axes
axes1 = axes('Parent',figure1,...
 'Position',[0.0604727522902636 0.127405098695899 0.877872619829284 
0.823712948517941]);
axis off
hold(axes1,'on');
% 创建 image
image(cdata1,'Parent',axes1);
% 取消以下行的注释以保留坐标轴的 X 范围
% xlim(axes1,[0.5 2005.5]);
% 取消以下行的注释以保留坐标轴的 Y 范围
% ylim(axes1,[0.5 792.5]);
box(axes1,'on');
axis(axes1,'ij');
% 设置其余坐标轴属性
set(axes1,'DataAspectRatio',[1 1 1],'Layer','top','TickDir','out');

function createfigure(cdata1)
%CREATEFIGURE(CDATA1)
% CDATA1: image cdata
% 由 MATLAB 于 08-May-2022 17:19:36 自动生成
% 创建 figure
figure1 = figure;
% 创建 axes
axes1 = axes('Parent',figure1,...
 'Position',[0.0683234434258691 0.0936544360826505 0.862017804154303 
0.870412844036697]);
axis off
hold(axes1,'on');
% 创建 image
image(cdata1,'Parent',axes1);
% 取消以下行的注释以保留坐标轴的 X 范围
% xlim(axes1,[0.5 2323.5]);
% 取消以下行的注释以保留坐标轴的 Y 范围
% ylim(axes1,[0.5 1517.5]);
box(axes1,'on');
axis(axes1,'ij');
% 设置其余坐标轴属性
set(axes1,'DataAspectRatio',[1 1 1],'Layer','top','TickDir','out');

function createfigure(cdata1)
%CREATEFIGURE(CDATA1)
% CDATA1: image cdata
% 由 MATLAB 于 08-May-2022 17:21:03 自动生成
% 创建 figure
figure1 = figure;
% 创建 axes
axes1 = axes('Parent',figure1,...
 'Position',[0.0931243698059368 0.224977047559425 0.811931243680485 
0.68870523415978]);
axis off
hold(axes1,'on');
% 创建 image
image(cdata1,'Parent',axes1);
% 取消以下行的注释以保留坐标轴的 X 范围
% xlim(axes1,[0.5 803.5]);
% 取消以下行的注释以保留坐标轴的 Y 范围
% ylim(axes1,[0.5 250.5]);
box(axes1,'on');
axis(axes1,'ij');
% 设置其余坐标轴属性
set(axes1,'DataAspectRatio',[1 1 1],'Layer','top','TickDir','out');

function createfigure(cdata1)
%CREATEFIGURE(CDATA1)
% CDATA1: image cdata
% 由 MATLAB 于 08-May-2022 17:22:22 自动生成
% 创建 figure
figure1 = figure;
% 创建 axes
axes1 = axes('Parent',figure1,...
 'Position',[0.0663544681110025 0.135884639374494 0.865994236311239 
0.81198003327787]);
axis off
hold(axes1,'on');
% 创建 image
image(cdata1,'Parent',axes1);
% 取消以下行的注释以保留坐标轴的 X 范围
% xlim(axes1,[0.5 1202.5]);
% 取消以下行的注释以保留坐标轴的 Y 范围
% ylim(axes1,[0.5 488.5]);
box(axes1,'on');
axis(axes1,'ij');
% 设置其余坐标轴属性
set(axes1,'DataAspectRatio',[1 1 1],'Layer','top','TickDir','out');