【笔记6-1】数据挖掘:推荐算法
【笔记6-1】数据挖掘:推荐算法
- (一)推荐算法概述
- (二)推荐相关算法介绍
-
- 1. TF-IDF
- 2. 向量空间模型(Vector Space Model)
- 3. 隐含语义分析(LSA, Latent Semantic Analysis)
- 4. PageRank
- 5. 协同过滤
清华大学【数据挖掘:推荐算法】
https://www.bilibili.com/video/av38554878
(一)推荐算法概述
- 为什么需要推荐算法
当前人们生活的社会信息含量巨大,称为信息过载(information overload)在这样的背景下,人们需要从海量的数据中高效的获取与自己最相关的部分,就需要借助推荐算法。
- 什么是推荐系统
用来预测用户对商品的排序和偏好的系统,是数据挖掘技术中最常见的应用实例。一个好的推荐算法甚至能为用户推荐他从来没有见过或者想过要搜索的商品,且该商品是用户感兴趣的或者是能为用户提供帮助的。
- 推荐系统的种类
基于内容的过滤:关注商品本身的特点,根据用户以往喜欢的商品,推荐类似的商品。
协同过滤:基于用户之间的相似性进行推荐
- 实例
精准广告投放(target advertisement,根据用户信息进行精准推荐)
精准音乐推荐(根据用户行为习惯分析用户喜好)
(二)推荐相关算法介绍
1. TF-IDF
- 应用场景:给定一个搜索关键词以及一系列内容,计算两者之间的相关度
- TF:term frequency,词频,表示词汇在文档中出现的频率
t f ( t , d ) = n t , d ∑ k n k , d tf(t,d)=\frac{n_{t,d}}{\sum_k n_{k,d}} tf(t,d)=∑knk,dnt,d - IDF:inverse document frequency,逆文档频率,利用词汇在不同文档中出现的次数计算词汇重要性。分母表示词汇在不同文档中出现过的文档数,分子为文档总数,分母越大说明词汇在多个文档中都有出现,对应的词汇重要性越低,逆文档频率也就越低。
i d f ( t , D ) = l o g ∣ D ∣ ∣ { d ∈ D : t ∈ d } ∣ idf(t,D)=log \frac{|D|}{|\{d\in D:t\in d\}|} idf(t,D)=log∣{d∈D:t∈d}∣∣D∣ - TF-IDF:同时取决于TF和IDF,说明词汇在文档中出现频率高的同时,要在其他文档中出现地少,才属于重要词汇。一般会构建 term-document matrix 来进行计算。 t f − i d f ( t , d , D ) = t f ( t , d ) ∗ i d f ( t , D ) tf-idf(t,d,D)=tf(t,d)*idf(t,D) tf−idf(t,d,D)=tf(t,d)∗idf(t,D)
2. 向量空间模型(Vector Space Model)
计算机无法直接对文本进行处理,往往需要将文本进行向量形式的表示: p = ( w 1 , p , w 2 , p , . . . , w t , p ) p=(w_{1,p},w_{2,p},...,w_{t,p}) p=(w1,p,w2,p,...,wt,p)向量中的每一维代表一个关键词,可以用0,1代表该关键词在文中是否出现,也可以用关键词出现的次数,或者直接用词汇的tf-idf。
在得到每个文档的向量表示之后,就可以利用向量的一些运算方法来计算文本之间的余弦相似度: s i m ( p , q ) = c o s ( θ ) = p ⋅ q ∣ p ∣ ⋅ ∣ q ∣ sim(p,q)=cos(\theta)=\frac{p\cdot q}{|p|\cdot|q|} sim(p,q)=cos(θ)=∣p∣⋅∣q∣p⋅q两个文本越相似,其向量表示之间的夹角越小,对应的余弦相似度就越大。
但是,直接利用tf-idf来计算文本相似性存在一定的缺陷,对于同义词或者多义词的情况,就会对计算的结果产生影响。(同义词可能导致召回率低,多义词则可能导致准确率低)为了解决这一问题,提出了新的解决方法如SVD,矩阵分解对文本进行降维表示。
3. 隐含语义分析(LSA, Latent Semantic Analysis)
X = T S D T X : m ∗ n ; T : m ∗ r ; S : r ∗ r ; D : n ∗ r ; r = r a n k ( X ) X=TSD^T \\ X: m*n; \ T: m*r; \ S: r*r; \ D:n*r; \ r=rank(X) X=TSDTX:m∗n; T:m∗r; S:r∗r; D:n∗r; r=rank(X)上式意味着文本的矩阵表示可以进行矩阵分解,得到正交矩阵 T , D T,D T,D 和对角矩阵 S S S,其中 T T T 可以理解为Term, D D D 则可以理解为Document。对矩阵分解得到的结果进行运算,可以得到词汇 term 和文档 document 的一些相关性质: X X T = ( T S D T ) ( T S D T ) T = T S D T D S T T T = T ( S S T ) T T XX^T=(TSD^T)(TSD^T)^T=TSD^TDS^TT^T=T(SS^T)T^T XXT=(TSDT)(TSDT)T=TSDTDSTTT=T(SST)TT首先将 X X X 与 X T X^T XT 求点积,即词汇 term 的点积,得到的结果可以解释为对 X X T XX^T XXT 进行特征分解的结果,对应的 T T T 为 X X T XX^T XXT 的特征向量, T S TS TS 的每一行则为每个 term 的坐标。
X T X = ( T S D T ) T ( T S D T ) = D S T T T T S D T = D ( S T S ) D T X^TX=(TSD^T)^T(TSD^T)=DS^TT^TTSD^T=D(S^TS)D^T XTX=(TSDT)T(TSDT)=DSTTTTSDT=D(STS)DT类似的,将 X T X^T XT 与 X X X 求点积,即文档 document 的点积,得到的结果可以解释为对 X T X X^TX XTX 进行特征分解的结果,对应的 D D D 为 X T X X^TX XTX 的特征向量, D S DS DS 的每一行则为每个 document 的坐标。
用一个实际的例子来对上述过程进行更直观的解释:

上述为本例中所使用的文本集,其中前五个样本为一类,剩下四个样本为一类。将其提取关键词并整理成 term-document matrix 可得:

对上述矩阵进行正交分解 X = T S D T X=TSD^T X=TSDT 可以得到前述, T , S , D T,S,D T,S,D 矩阵(该部分可以用MATLAB进行求解,直接得到对应的矩阵运算结果):
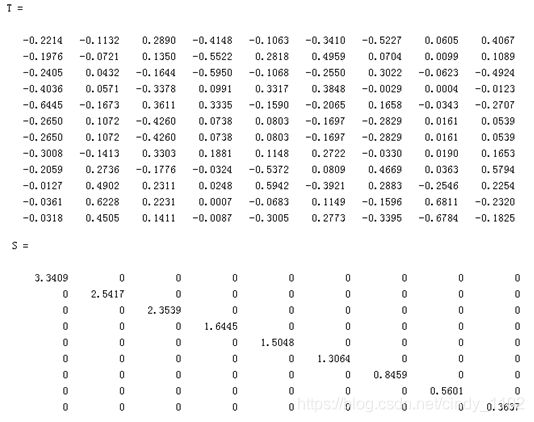

可以检验得到上述三个矩阵相乘确实是原来的 term-document matrix。观察上述 S 矩阵可以发现矩阵对角线上的元素按照从大到小的顺序进行排列,这和PCA降维的原理是类似的,前述较大的元素可以反映原始矩阵较多的信息,此外,为了方便可视化,选取前两维进行分析:

上述选取的前两维 T 和 D 进行可视化可以分别表示 term 和 document 在二维空间中的位置,对二维空间中各样本的位置求余弦相似度可以得到各个 term 以及 document 之间的相似度,可视化结果表明相似的文本确实会被聚集到一起:

4. PageRank
PageRank 是一种用于评估包含超链接的网页的重要性的方法,该方法将指向某一网页的超链接视为肯定该网页内容的一次有效投票,最终网页的重要性评估将同时取决于网页的 PageRank 以及网页包含的外指超链接数量。
需要注意的是,PageRank 看重的是指向某一网页的超链接数量,而不是该网页指向其他网页的超链接数量,因为前者是网页本身不可控制的,而后者则是可以操纵的。
网页的 PageRank 计算方法可以表示为: P R ( p i ) = ∑ p j ∈ M ( p i ) P R ( p j ) L ( p j ) PR(p_i)=\sum_{p_j\in M(p_i)}\frac{PR(p_j)}{L(p_j)} PR(pi)=pj∈M(pi)∑L(pj)PR(pj) 其中 L ( p j ) L(p_j) L(pj) 表示由网页 p j p_j pj 指向其他网页的链接数, M ( p i ) M(p_i) M(pi) 表示指向 p i p_i pi 的网页的集合,更具体地,用下述例子来解释上述计算过程:
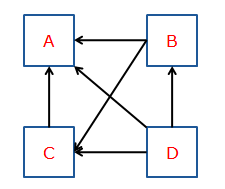
由上图可知,指向网页A的有B,C,D三个网页,其中由B指出的网页有2个,由C指出的有1个,由D指出的有三个,因此A的PageRank可以表示为: P R ( A ) = P R ( B ) 2 + P R ( C ) 1 + P R ( D ) 3 PR(A)=\frac{PR(B)}{2}+\frac{PR(C)}{1}+\frac{PR(D)}{3} PR(A)=2PR(B)+1PR(C)+3PR(D)考虑输入网址进行跳转的情况,假设用户继续浏览某一网页的概率为 d,输入网址直接进行网页跳转的概率则为 1-d,于是,上述计算方法可以转换为: P R ( p i ) = 1 − d N + d ∑ p j ∈ M ( p i ) P R ( p j ) L ( p j ) PR(p_i)=\frac{1-d}{N}+d\sum_{p_j\in M(p_i)}\frac{PR(p_j)}{L(p_j)} PR(pi)=N1−d+dpj∈M(pi)∑L(pj)PR(pj)直观解释则为用户直接输入网址的概率为 1-d,总共有N个网址,因此跳转到 p i p_i pi 的概率为 1 − d N \frac{1-d}{N} N1−d,其他情况下则为用户浏览网页之后点击链接完成网页跳转。
5. 协同过滤
核心思想:相似用户之间的推荐
一般步骤:构造评分/购买矩阵 --> 通过评分对相似用户进行匹配 --> 向用户推荐其他相似用户评分高的产品
类别:
- 基于记忆的协同过滤:基于用户 vs 基于内容
- 基于模型的协同过滤
协同过滤中的难点:
- gray sheep:存在某些用户与其他任何用户都不相似,无法进行类似用户之间的推荐
- shilling attack:评分水军导致真实数据缺失
- cold start:冷启动问题,对于新用户和新商品难以获得相关评分信息
基于用户的协同过滤:
w u , v = ∑ i ∈ I ( r u , i − r ˉ u ) ( r v , i − r ˉ v ) ∑ i ∈ I ( r u , i − r ˉ u ) 2 ∑ i ∈ I ( r v , i − r ˉ v ) 2 w_{u,v}=\frac{\sum_{i\in I}(r_{u,i}-\bar r_u)(r_{v,i}-\bar r_v)}{\sqrt{\sum_{i \in I}(r_{u,i}-\bar r_u)^2}\sqrt{\sum_{i\in I}(r_{v,i}-\bar r_v)^2}} wu,v=∑i∈I(ru,i−rˉu)2∑i∈I(rv,i−rˉv)2∑i∈I(ru,i−rˉu)(rv,i−rˉv) P a , i = r ˉ a + ∑ u ∈ U ( r u , i − r ˉ u ) ⋅ w a , u ∑ u ∈ U ∣ w a , u ∣ P_{a,i}=\bar r_a+\frac{\sum_{u \in U}(r_{u,i}-\bar r_u)\cdot w_{a,u}}{\sum_{u\in U}|w_{a,u}|} Pa,i=rˉa+∑u∈U∣wa,u∣∑u∈U(ru,i−rˉu)⋅wa,u示例:
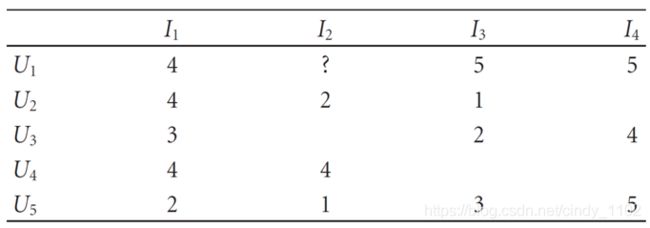
如果我们需要预测上述情况下用户1对于商品2的评分,就可以借助上面提供的公式进行计算。
需要注意的是,在计算当前客户的平均评分时,只考虑该客户有评分的部分,而在计算两个用户之间的相关变量计算时,只考虑两个用户都有评分的部分,比如下列步骤:
P 1 , 2 = r ˉ 1 + ∑ u ( r u , 2 − r ˉ u ) ⋅ w 1 , u ∑ u ∣ w 1 , u ∣ = r ˉ 1 + ( r 2 , 2 − r ˉ 2 ) w 1 , 2 + ( r 4 , 2 − r ˉ 4 ) w 1 , 4 + ( r 5 , 2 − r ˉ 5 ) w 1 , 5 ∣ w 1 , 2 ∣ + ∣ w 1 , 4 ∣ + ∣ w 1 , 5 ∣ = 4.67 + ( 2 − 2.5 ) ( − 1 ) + ( 4 − 4 ) 0 + ( 1 − 3.33 ) 0.756 1 + 0 + 0.756 = 3.95 \begin{aligned} P_{1,2}&=\bar r_1+\frac{\sum_u(r_{u,2}-\bar r_u)\cdot w_{1,u}}{\sum_u |w_{1,u}|}\\&=\bar r_1+\frac{(r_{2,2}-\bar r_2)w_{1,2}+(r_{4,2}-\bar r_4)w_{1,4}+(r_{5,2}-\bar r_5)w_{1,5}}{|w_{1,2}|+|w_{1,4}|+|w_{1,5}|}\\&=4.67+\frac{(2-2.5)(-1)+(4-4)0+(1-3.33)0.756}{1+0+0.756}\\&=3.95 \end{aligned} P1,2=rˉ1+∑u∣w1,u∣∑u(ru,2−rˉu)⋅w1,u=rˉ1+∣w1,2∣+∣w1,4∣+∣w1,5∣(r2,2−rˉ2)w1,2+(r4,2−rˉ4)w1,4+(r5,2−rˉ5)w1,5=4.67+1+0+0.756(2−2.5)(−1)+(4−4)0+(1−3.33)0.756=3.95更具体的计算步骤如下: r ˉ 1 = 4 + 5 + 5 3 = 4.67 \bar r_1=\frac{4+5+5}{3}=4.67 rˉ1=34+5+5=4.67 r ˉ 2 = 4 + 1 2 \bar r_2=\frac{4+1}{2} rˉ2=24+1 w 1 , 2 = ∑ i ∈ I ( r 1 , i − r ˉ 1 ) ( r 2 , i − r ˉ 2 ) ∑ i ∈ I ( r 1 , i − r ˉ 1 ) 2 ∑ i ∈ I ( r 2 , i − r ˉ 2 ) 2 = ( 4 − 4.5 ) ( 4 − 2.5 ) + ( 5 − 4.5 ) ( 1 − 2.5 ) ( 4 − 4.5 ) 2 + ( 5 − 4.5 ) 2 ( 4 − 2.5 ) 2 ( 1 − 2.5 ) 2 = ( − 0.5 ) ( 1.5 ) + ( 0.5 ) ( − 1.5 ) 2 ∗ 0.5 ∗ 1.5 = − 1 \begin{aligned} w_{1,2}&=\frac{\sum_{i\in I}(r_{1,i}-\bar r_1)(r_{2,i}-\bar r_2)}{\sqrt{\sum_{i \in I}(r_{1,i}-\bar r_1)^2}\sqrt{\sum_{i\in I}(r_{2,i}-\bar r_2)^2}} \\&=\frac{(4-4.5)(4-2.5)+(5-4.5)(1-2.5)}{\sqrt{(4-4.5)^2+(5-4.5)^2}\sqrt{(4-2.5)^2(1-2.5)^2}}\\&=\frac{(-0.5)(1.5)+(0.5)(-1.5)}{2*0.5*1.5}=-1 \end{aligned} w1,2=∑i∈I(r1,i−rˉ1)2∑i∈I(r2,i−rˉ2)2∑i∈I(r1,i−rˉ1)(r2,i−rˉ2)=(4−4.5)2+(5−4.5)2(4−2.5)2(1−2.5)2(4−4.5)(4−2.5)+(5−4.5)(1−2.5)=2∗0.5∗1.5(−0.5)(1.5)+(0.5)(−1.5)=−1
基于内容的协同过滤:
w i , j = ∑ u ∈ U ( r u , i − r ˉ i ) ( r u , j − r ˉ j ) ∑ u ∈ U ( r u , i − r ˉ i ) 2 ∑ u ∈ U ( r u , j − r ˉ j ) 2 w_{i,j}=\frac{\sum_{u\in U}(r_{u,i}-\bar r_i)(r_{u,j}-\bar r_j)}{\sqrt{\sum_{u\in U}(r_{u,i}-\bar r_i)^2}\sqrt{\sum_{u \in U}(r_{u,j}-\bar r_j)^2}} wi,j=∑u∈U(ru,i−rˉi)2∑u∈U(ru,j−rˉj)2∑u∈U(ru,i−rˉi)(ru,j−rˉj)其中, U U U 表示同时对商品 i 和 j 进行了打分的用户集合。 P a , i = ∑ j ∈ I w i , j ⋅ r a , j ∑ j ∈ I ∣ w i , j ∣ P_{a,i}=\frac{\sum_{j \in I}w_{i,j}\cdot r_{a,j}}{\sum_{j \in I}|w_{i,j}|} Pa,i=∑j∈I∣wi,j∣∑j∈Iwi,j⋅ra,j其中, I I I 表示所有被用户 a 进行过评分的商品集合。
P a , i = r ˉ a + 1 ∣ U ∣ ∑ u ∈ U ( r u , i − r ˉ u ) P_{a,i}=\bar r_a+\frac{1}{|U|}\sum_{u\in U}(r_{u,i}-\bar r_u) Pa,i=rˉa+∣U∣1u∈U∑(ru,i−rˉu)其中, U U U 表示所有对商品 i 进行过打分的用户集合。 d e v i , j = 1 ∣ U ∣ ∑ u ∈ U ( r u , i − r u , j ) dev_{i,j}=\frac{1}{|U|}\sum_{u \in U}(r_{u,i}-r_{u,j}) devi,j=∣U∣1u∈U∑(ru,i−ru,j)其中, U U U 表示对商品 i 和 j 都进行过打分的用户集合。 P a , i = 1 ∣ I ∣ ∑ j ∈ I ( d e v i , j + r a , j ) P_{a,i}=\frac{1}{|I|}\sum_{j \in I}(dev_{i,j}+r_{a,j}) Pa,i=∣I∣1j∈I∑(devi,j+ra,j)其中, I I I 是用户评过分且具有 dev 值的商品集合。
示例:
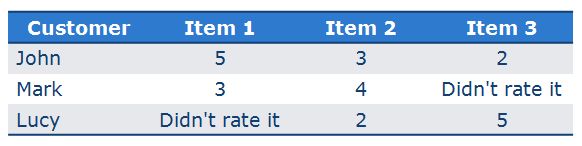
根据用户对平均分的偏离进行预测: P L u c y , 1 = 2 + 5 2 + 5 − 2.5 + 3 − 4 2 = 4.25 P_{Lucy,1}=\frac{2+5}{2}+\frac{5-2.5+3-4}{2}=4.25 PLucy,1=22+5+25−2.5+3−4=4.25比较商品之间的评分差距进行预测: d e v 1 , 2 = 2 − 1 2 = 0.5 , d e v 1 , 3 = 3 1 = 3 dev_{1,2}=\frac{2-1}{2}=0.5 ,\ dev_{1,3}=\frac{3}{1}=3 dev1,2=22−1=0.5, dev1,3=13=3 P L u c y , 1 = 1 2 ( 0.5 + 2 + 3 + 5 ) = 5.25 P_{Lucy,1}=\frac{1}{2}(0.5+2+3+5)=5.25 PLucy,1=21(0.5+2+3+5)=5.25考虑打分的人数作为权重: P L u c y , 1 = 2 ∗ 2.5 + 1 ∗ 8 2 + 1 = 4.33 P_{Lucy,1}=\frac{2*2.5+1*8}{2+1}=4.33 PLucy,1=2+12∗2.5+1∗8=4.33
基于模型的协同过滤:
基于模型的协同过滤可以将有打分的部分作为训练集,将需要预测的部分作为测试集。模型的输入为其他用户的打分,输出则为目标用户的打分(可以视为分类问题)。在具体的计算过程中可以训练多种分类器,如基于朴素贝叶斯的分类器。

