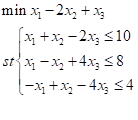线性与非线性规划——单纯形法python实现
线性与非线性规划——单纯形法python实现
单纯形法原理及python实现，时间：2022/1/11
本文不对单纯形方法进行讲解，若有需要请参照《最优化理论与算法第二版》（陈宝林著），或参照下方链接了解单纯形的基本概念简单易懂的单纯形法理解
代码实现是参照单纯形表，先把表放这待会可以对比来看：
上图是单纯形表各个位置所代表的数的计算方法，单纯形法将A矩阵分为[B,N]，B一般为单位阵，cB表示xB前的系数，cN为xN前的系数，下面用实际算例进行说明。
- 读取数据
#这里的A1为约束左边自变量系数，b1为约束右边，c1为目标函数中x前系数，格式如下
matrix_A = np.loadtxt('./A1.txt')
matrix_b = np.loadtxt('./b1.txt')
matrix_c = np.loadtxt('./c1.txt')
2. 标准化并生成单纯形表
将上式标准化后得到：
基于上述式子得到单纯形表：
def convert_save(matrix_A,matrix_b,matrix_c): # matrix_A:{n,m},matrix_b:{1,n},matrix_c:{1,m}
add = np.diag(np.ones(len(matrix_A)))
matrix_b = matrix_b.reshape(-1,1)
matrix_A = np.hstack((matrix_A,add,matrix_b)) #补充松弛变量建立系数矩阵
matrix_sigma = np.hstack((-matrix_c,np.zeros(matrix_A.shape[1]-matrix_c.shape[0]))) # 检验数向量
final_matrix =np.vstack((matrix_A,matrix_sigma))
np.save('./matrix',final_matrix)
print('successfu; create matrix') #保存单纯形表
输出为：
3. 进行单纯形法流程迭代（直接上代码！）
首先是单纯形表进行一次计算的程序（包括找基变量以及消元操作）
def calcu(M): #M为单纯形表
(m,n) = M.shape
l = list(M[-1,:-1])
target_n = l.index(max(l)) #列编号
# 确定主元
A = np.array([M[x,-1] for x in range(m-1) if M[x,target_n]>=0])/(np.array([x for x in M[:-1,target_n] if x >=0])+0.00001)
label = [l for l in range(m-1) if M[l,target_n]>=0]
target_m = label[np.argmin(A)] #行编号
# 进行消元操作
r = M[target_m][target_n]
M[target_m] /= r #主元系数变为1
for i in [x for x in range(m) if x!= target_m]:
r = M[i][target_n]
M[i] -= r* M[target_m]
下面是进行循环迭代
def solve(M):
flag = True
while flag:
if max(list(M[-1][:-2])) <= 0: #找到最终解
flag = False
else:
calcu(M)
- 最终代码
下面代码有求最大值和最小值两种情况，注释中已清楚表明。
# -*- coding: utf-8 -*-
"""
Created on Mon Dec 13 11:22:12 2021
@author: nanase
"""
import numpy as np
def convert_save(matrix_A,matrix_b,matrix_c): # matrix_A:{n,m},matrix_b:{1,n},matrix_c:{1,m}
add = np.diag(np.ones(len(matrix_A)))
matrix_b = matrix_b.reshape(-1,1)
matrix_A = np.hstack((matrix_A,add,matrix_b)) #补充松弛变量建立系数矩阵
matrix_sigma = np.hstack((-matrix_c,np.zeros(matrix_A.shape[1]-matrix_c.shape[0]))) # 检验数向量
final_matrix =np.vstack((matrix_A,matrix_sigma))
np.save('./matrix',final_matrix)
print('successfu; create matrix')
def calcu(M):
(m,n) = M.shape
l = list(M[-1,:-1])
target_n = l.index(max(l))
# 确定主元
A = np.array([M[x,-1] for x in range(m-1) if M[x,target_n]>=0])/(np.array([x for x in M[:-1,target_n] if x >=0])+0.00001)
label = [l for l in range(m-1) if M[l,target_n]>=0]
target_m = label[np.argmin(A)] #行编号
# 进行消元操作
r = M[target_m][target_n]
M[target_m] /= r #主元系数变为1
for i in [x for x in range(m) if x!= target_m]:
r = M[i][target_n]
M[i] -= r* M[target_m]
def solve(M):
flag = True
while flag:
if max(list(M[-1][:-2])) <= 0:
flag = False
else:
calcu(M)
def printRe(M):
(m,n) = M.shape
result = np.zeros(n-1)
#找最优值，注意一一对应
for i in range(m-1):
target_n = [j for j in range(n) if M[i,j] == 1 and M[-1,j] == 0]
# target_n = list(M[i]).index(1)
result[target_n] = M[i,-1]
print(f'最终结果为：{result},最优值为：{M[-1,-1]}')
#算例1
matrix_A = np.loadtxt('./A1.txt')
matrix_b = np.loadtxt('./b1.txt')
matrix_c = np.loadtxt('./c1.txt')
#算例2
# matrix_A = np.loadtxt('./A2.txt')
# matrix_b = np.loadtxt('./b2.txt')
# matrix_c = np.loadtxt('./c2.txt')
mode = 1 #1为求最小值，2为求最大值
if mode == 1:
convert_save(matrix_A,matrix_b,matrix_c)
M = np.load('./matrix.npy')
solve(M)
printRe(M)
elif mode == 2:
matrix_c = -matrix_c
convert_save(matrix_A,matrix_b,matrix_c)
M = np.load('./matrix.npy')
solve(M)
M[-1,-1] = -M[-1,-1]
printRe(M)
欢迎大佬们批评指正。