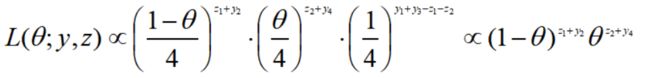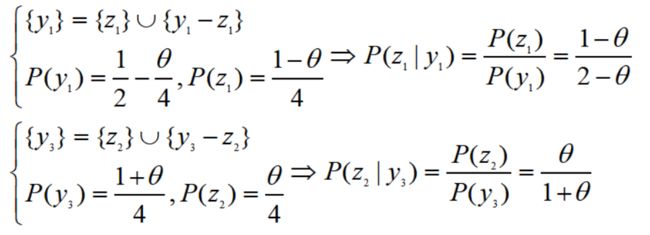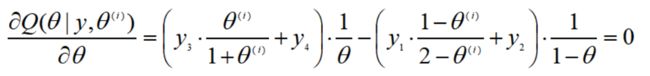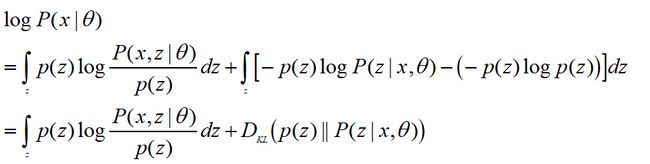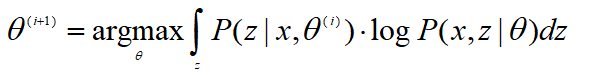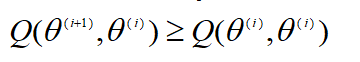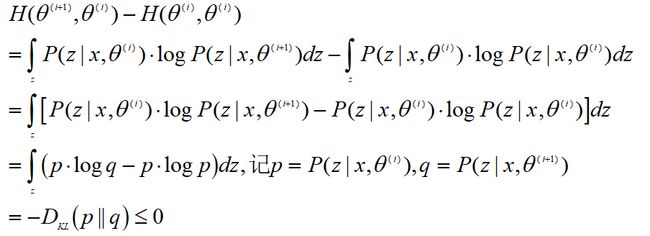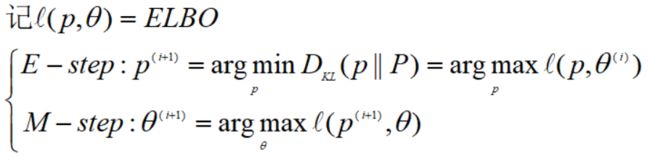EM算法

1.EM算法，称为期望-最大化，它用于求解MLE的一种迭代算法

2.它的主要思想是把一个难于处理的似然函数最大化问题用一个易于最大化的序列取代，而其极限是原始问题的解

3.EM算法分两步走：E步求期望，对隐变量进行积分；M步求参数最大值

4.推导出EM算法有两个途径：ELBO+KL散度和ELBO+Jensen不等式

5.一般情况下，EM算法是收敛的

6.E步本质是求隐变量z的后验分布p(z|x,θ)，但很多情况无法直接求解，这就引出广义EM算法

7.广义EM的E步是求KL散度最小值的p(z)，M步求似然函数最大值的参数θ

8.广义EM算法也无法求解所有最优化问题，这时会有变种的EM算法，比如变分推断、蒙特卡洛采样等

EM算法（Expectation-Maximization），中文是期望-最大化。它是求解估计量的一种方法，用于保证收敛到MLE（最大似然估计）。主要用于求解包含隐变量的混合模型，主要思想是把一个难于处理的似然函数最大化问题用一个易于最大化的序列取代，而其极限是原始问题的解。

注：MLE传送门——最大似然估计

我们从一个例子介绍EM算法的思想。

例子引入

设一次试验可能有四个结果，其发生的概率分别为1/2-θ/4,(1-θ)/4,(1+θ)/4,θ/4,其中θ∈(0,1)。现进行了197次试验，四种结果发生的次数分别为75，18，70，34.试求θ的MLE.

利用MLE求解其参数，以y1,y2,y3,y4表示四种结果发生的次数，此时总体分布为多项分布，故其似然函数为：

直接求解θ的MLE显然比较麻烦，因为其对数似然方程是一个三次多项式.

我们通过引入2个变量z1,z2使得求解变得容易。现假设第一种结果分成两部分，其发生概率分别为(1-θ)/4和1/4，令z1和y1-z1是落入这两部分的次数：

P(概率)	(1-θ)/4	1/4
N(发生次数)	z1	y1-z1

第三种结果也分成两部分，发生概率分别为θ/4和1/4，令z2和y3-z2是落入这两部分的次数：

P(概率)	θ/4	1/4
N(发生次数)	z2	y3-z2

其中，z1和z2称为潜变量（隐变量）,它是不可观测的。称（y,z)为完全数据，能观测到的y为不完全数据。此时，完全数据的似然函数为：

其对数似然：

现在，我们仅知道y，而无法得知z。注意到当给定θ和y时，z1和z2服从二项分布：

因为，

根据这个信息，天才数学家想出了求解θ的方法，这就是EM算法，它分两步走。

E步：在已有观测数据y及第i步估计值θ=θi的条件下，求基于完全数据的对数似然函数的期望（把有关z的部分积分掉）

M步：求基于第i步期望的最大化参数θ(i+1)，也就是

重复上面的E步和M步，直至收敛，即完成了θ的MLE估计。

对于本例，E步为：

M步为对上式求导并置为0：

最终解得

取初始值0.5，我们迭代12次左右参数θ收敛。于是得到θ的MLE解为0.60675

算法定义

这一节我们正式推导EM算法，先直接给结论，EM算法迭代公式：

其中，E步和M步分别是：

我们把(x,z)称为完全数据，x是可观测的变量，z是隐变量，θ是要估计的参数

推导出该公式有两个角度，一个是KL散度角度，一个是Jensen不等式角度，我们分别介绍。

• ELBO+KL散度

根据MLE，我们有对数似然函数：

引入隐变量z，我们得到：

看不懂？计算过程如下：

等式两边同时乘以p(z)：

做积分与恒等变换有：

化简一下：

这里利用了KL散度(交叉熵-熵)的公式，散度必定大于等于0。不熟悉的伙伴请回顾文章：WOE编码与IV值、机器学习之模型评估（损失函数）

所以我们有：

把不等式右边部分称为ELBO(evidence lower bound).

等号成立的条件是散度为0，即要满足：

这个是z的后验，记第i次迭代的后验

则有：

要求ELBO的最大值：

于是我们推导出了参数迭代公式：

• ELBO+Jensen
  

我们利用Jensen不等式也可以推出EM公式。

Jensen不等式：

若f(x)是凸函数，则下面不等式成立：

根据联合概率分布求边缘概率，我们有

仔细观测一下，不等式右边就是ELBO，于是

ELBO为似然函数的下确界，要使得似然函数最大，只要保证等号成立且ELBO取得最大，即：

做个变换有：

于是p(z)为后验。后面求最值与前面一样，不再赘述。

收敛性证明

最后我们不是特别严格的证明一下EM算法收敛性问题。根据上一小节我们得到：

假设第i步我们得到参数θ值，根据已有观测数据，我们有：

等式两边同时对z求积分，有：

为了方便，我们记

假设

那么有

这个显然成立，同时，

因此，我们有：

最终我们得到

这个称为EM算法的收敛性证明

广义EM算法

根据前面的推导，我们知道似然函数等于ELBO+KL散度：

其迭代公式为:

E步与M步是：

由上面可知，EM算法的E步的关键是对隐变量求积分，求解其后验分布p(z):

本文开头的例子，我们知道隐变量z1和z2的分布，故容易求解其后验。但在现实中，很多情况无法直接求解后验分布。这个时候就需要用到近似推断的方法，比如变分推断和蒙特卡洛采样。

我们把适用更一般情况的EM算法称为广义EM算法，用数学符号表达为：

这里一开始把θi固定，那么ELBO+KL为常数，要使得ELBO最大，只需要KL最小，也即找到使得KL最小的p(z)，这是E步；接着固定p(z)，找到使得ELBO最大的θ(i+1)。

这种思想先固定一个，再求一个参数的方法叫做坐标上升法，也就是我们在支持向量机系列讲到的SMO算法。

最后，E步和M步有时候都很难求解，我们会引出更多EM算法的变种，主要是变分推断和蒙特卡洛采样方法。以后小编会出文章专门介绍。

参考资料：

《概率论与数理统计第二版》