回归算法-线性回归分析

回归算法-线性回归分析

线性关系模型----一个通过属性的线性组合来进行预测的函数：

线性回归：

通过一个或者多个自变量与因变量之间进行建模的回归分析。

其中特点为一个或多个回归系数的模型参数的线性组合

一元线性回归：涉及到的变量只有一个

多元线性回归：涉及到的变量两个或两个以上

损失函数(误差大小)

注：损失函数，用来度量预测值和实际值之间的差异，它是一个非负实值函数，从而作为模型性能参考依据。

损失值越小，说明预测输出和实际结果之间的差值就越小，也就说明构建的模型越好，反之说明模型越差。

如何去求模型当中的W，使得损失（误差）最小？

1）最小二乘法之正规方程（只适用于简单的线性回归）

2）最小二乘法之梯度下降

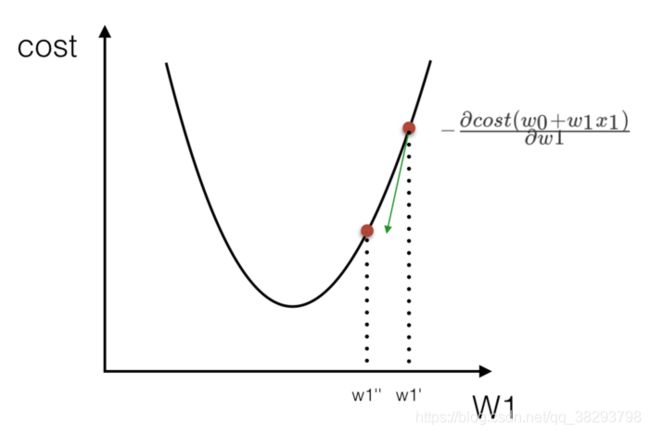
sklearn线性回归正规方程、梯度下降API：

sklearn.linear_model.LinearRegression----正规方程

sklearn.linear_model.SGDRegressor----梯度下降

语法：

sklearn.linear_model.LinearRegression()

普通最小二乘线性回归

coef_：回归系数

sklearn.linear_model.SGDRegressor( )

通过使用SGD最小化线性模型

coef_：回归系数

回归性能评估

(均方误差(Mean Squared Error)MSE) 评价机制：

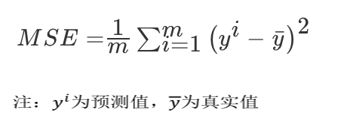
sklearn回归评估API: sklearn.metrics.mean_squared_error

方法：

mean_squared_error(y_true, y_pred)-----均方误差回归损失

y_true:真实值

y_pred:预测值

return:浮点数结果

注：真实值，预测值为标准化之前的值

LinearRegression与SGDRegressor评估

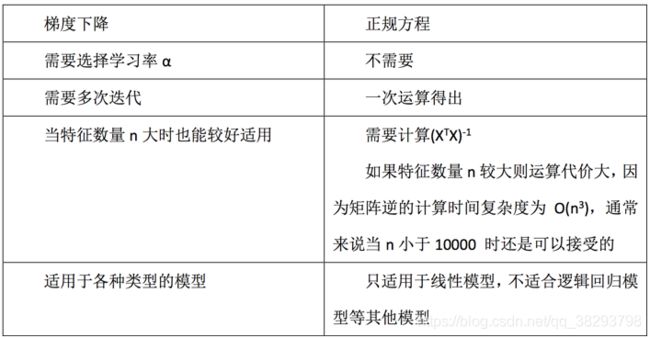
特点：线性回归器是最为简单、易用的回归模型。从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

小规模数据：LinearRegression(不能解决拟合问题)以及其它

大规模数据：SGDRegressor

案例–波士顿房价数据案例

分析流程：

1.波士顿地区房价数据获取

2.波士顿地区房价数据分割

3.训练与测试数据标准化处理

4.使用最简单的线性回归模型LinearRegression和梯度下降估计SGDRegressor对房价进行预测

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
def mylinner():
    """线性回归直接预测房子价格"""
    # 获取数据
    lb = load_boston()
    # 分割数据集为训练集和测试集 x:特征值 y:目标值
    x_train,x_test,y_train,y_test = train_test_split(lb.data,lb.target,test_size=0.25)
    # 进行标准化处理----特征值和目标值都必须进行标准化处理
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1,1))
    y_test = std_y.transform(y_test.reshape(-1,1))

    # estimator预测
    # 1.正规方程求解方式预测结果
    lr = LinearRegression()
    lr.fit(x_train,y_train)
    print("正规方程求解方式回归系数为：",lr.coef_)
    # 预测 测试集 房子价格
    y_lr_predict = lr.predict(x_test)
    y_lr_predict = std_y.inverse_transform(y_lr_predict)
    # y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    print("正规方程求解方式-测试集里每个房子的预测价格：",y_lr_predict)
    print("lr的均方误差为：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))

    # 2.使用梯度下降进行预测
    sgd = SGDRegressor()
    sgd.fit(x_train,y_train)
    print("梯度下降求解方式回归系数为：",sgd.coef_)
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print("使用梯度下降预测的房子价格：", y_sgd_predict)
    print("SGD的均方误差为：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

if __name__ == '__main__':
    mylinner()