【机器学习基础】判别函数
本系列为《模式识别与机器学习》的读书笔记。
一,分类线性模型概述
分类的⽬标是将输⼊变量 x \boldsymbol{x} x 分到 K K K 个离散的类别 C k \mathcal{C}_k Ck 中的某⼀类。 最常见的情况是, 类别互相不相交, 因此每个输⼊被分到唯⼀的⼀个类别中。因此输⼊空间被划分为不同的决策区域(decision region),它的边界被称为决策边界(decision boundary)或者决策⾯(decision surface)。
分类线性模型是指决策⾯是输⼊向量 x \boldsymbol{x} x 的线性函数,因此被定义为 D D D 维输⼊空间中的 ( D − 1 ) (D − 1) (D−1) 维超平⾯。如果数据集可以被线性决策⾯精确地分类,那么我们说这个数据集是线性可分的(linearly separable)。
在线性回归模型中,使⽤⾮线性函数 f ( ⋅ ) f(·) f(⋅) 对 w \boldsymbol{w} w 的线性函数进⾏变换,即
y ( x ) = f ( w T x + w 0 ) (4.1) y(\boldsymbol{x})=f(\boldsymbol{w}^{T}\boldsymbol{x}+w_0)\tag{4.1} y(x)=f(wTx+w0)(4.1)
在机器学习的⽂献中, f ( ⋅ ) f(·) f(⋅) 被称为激活函数(activation function),⽽它的反函数在统计学的⽂献中被称为链接函数(link function)。决策⾯对应于 y ( x ) = 常 数 y(\boldsymbol{x}) = 常数 y(x)=常数,即 w T x + w 0 = 常 数 \boldsymbol{w}^{T}\boldsymbol{x} + w_0 = 常数 wTx+w0=常数,因此决策⾯是 x \boldsymbol{x} x 的线性函数,即使函数 f ( ⋅ ) f(·) f(⋅) 是⾮线性函数也是如此。因此,由公式(4.1)描述的⼀类模型被称为推⼴的线性模型(generalized linear model)(McCullagh and Nelder, 1989)。
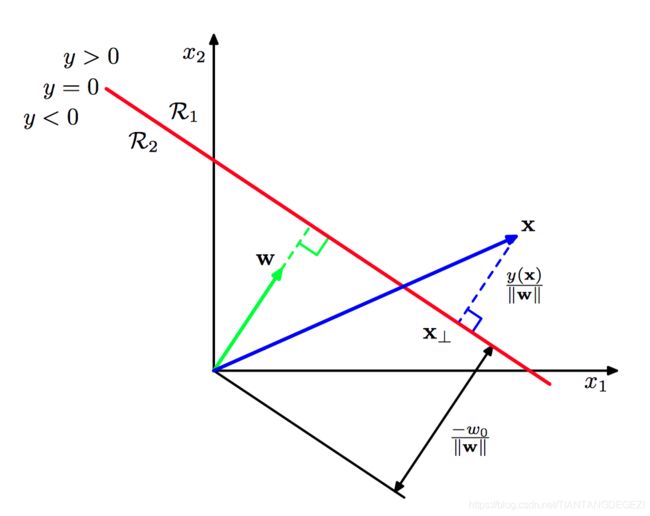
如图4.1,⼆维线性判别函数的⼏何表⽰。决策⾯(红⾊)垂直于 w \boldsymbol{w} w ,它距离原点的偏移量由偏置参数 w 0 w_0 w0 控制。
二,判别函数
判别函数是⼀个以向量 x \boldsymbol{x} x 为输⼊,把它分配到 K K K 个类别中的某⼀个类别(记作 C k \mathcal{C}_k Ck )的函数。
1,⼆分类
线性判别函数的最简单的形式是输⼊向量的线性函数,即
y ( x ) = w T x + w 0 (4.2) y(\boldsymbol{x})=\boldsymbol{w}^{T}\boldsymbol{x}+w_0\tag{4.2} y(x)=wTx+w0(4.2)
其中 w \boldsymbol{w} w 被称为权向量(weight vector), w 0 w_0 w0 被称为偏置(bias)。偏置的相反数有时被称为阈值(threshold)。
考虑两个点 x A \boldsymbol{x}_A xA 和 x B \boldsymbol{x}_B xB ,两个点都位于决策⾯上。 由于 y ( x A ) = y ( x B ) = 0 y(\boldsymbol{x}_A)=y(\boldsymbol{x}_B)=0 y(xA)=y(xB)=0,我们有 w T ( x A − x B ) = 0 \boldsymbol{w}^{T}(\boldsymbol{x}_A-\boldsymbol{x}_B) = 0 wT(xA−xB)=0,因此向量 w \boldsymbol{w} w 与决策⾯内的任何向量都正交,从⽽ w \boldsymbol{w} w 确定了决策⾯的⽅向。类似地,如果 x \boldsymbol{x} x 是决策⾯内的⼀个点,那么 y ( x ) = 0 y(\boldsymbol{x}) = 0 y(x)=0 ,因此从原点到决策⾯的垂直距离为
w T x ∥ w ∥ = − w 0 ∥ x ∥ (4.3) \frac{\boldsymbol{w}^{T}\boldsymbol{x}}{\|\boldsymbol{w}\|}=-\frac{w_0}{\|\boldsymbol{x}\|}\tag{4.3} ∥w∥wTx=−∥x∥w0(4.3)
其中,偏置参数 w 0 \boldsymbol{w}_0 w0 确定了决策⾯的位置。
记任意⼀点 x \boldsymbol{x} x 到决策⾯的垂直距离 r r r ,在决策⾯上的投影 x ⊥ \boldsymbol{x}_{\perp} x⊥ ,则有
x = x ⊥ + r w ∥ w ∥ (4.4) \boldsymbol{x}=\boldsymbol{x}_{\perp}+r \frac{\boldsymbol{w}}{\|\boldsymbol{w}\|}\tag{4.4} x=x⊥+r∥w∥w(4.4)
利用已知公式和 y ( x ⊥ ) = 0 y(\boldsymbol{x}_{\perp})=0 y(x⊥)=0 可得
r = y ( x ) ∥ w ∥ (4.5) r=\frac{y(\boldsymbol{x})}{\|w\|}\tag{4.5} r=∥w∥y(x)(4.5)
为方便简洁,引⼊“虚”输⼊ x 0 = 1 x_0=1 x0=1 ,并且定义 w ~ = ( w 0 , w ) \tilde{\boldsymbol{w}} = (w_0,\boldsymbol{w}) w~=(w0,w) 以及 x ~ = ( x 0 , x ) \tilde{\boldsymbol{x}} = (x_0,\boldsymbol{x}) x~=(x0,x) ,从⽽
y ( x ) = w ~ T x ~ (4.6) y(\boldsymbol{x})=\tilde{\boldsymbol{w}}^{T}\tilde{\boldsymbol{x}}\tag{4.6} y(x)=w~Tx~(4.6)
在这种情况下, 决策⾯是⼀个 D D D 维超平⾯, 并且这个超平⾯会穿过 D + 1 D+1 D+1 维扩展输⼊空间的原点。
2,多分类
考虑把线性判别函数推⼴到 K > 2 K>2 K>2 个类别。
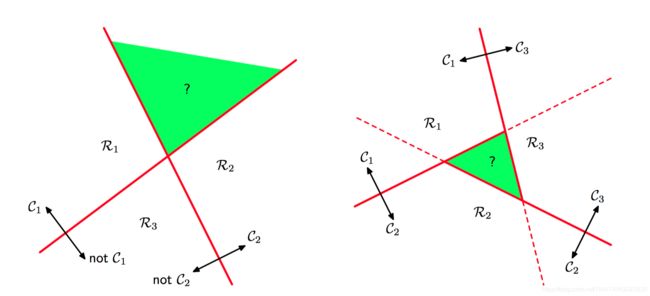
方法一,使⽤ K − 1 K − 1 K−1 个分类器,每个分类器⽤来解决⼀个⼆分类问题,把属于类别 C k \mathcal{C}_k Ck 和不属于那个类别的点分开。这被称为“1对其他”(one-versus-the-rest)分类器。此方法的缺点在于产⽣了输⼊空间中⽆法分类的区域。
方法二,引⼊ K ( K − 1 ) 2 \frac{K(K−1)}{2} 2K(K−1) 个⼆元判别函数, 对每⼀对类别都设置⼀个判别函数。 这被称为“1对1”(one-versus-one)分类器。每个点的类别根据这些判别函数中的⼤多数输出类别确定,但是,这也会造成输⼊空间中的⽆法分类的区域。
如图4.2,尝试从⼀组两类的判别准则中构建出⼀个 K K K 类的判别准则会导致具有奇异性的区域, ⽤绿⾊表⽰。
方法三,通过引⼊⼀个 K K K 类判别函数,可以避免上述问题。这个 K K K 类判别函数由 K K K 个线性函数组成,形式为
y k ( x ) = w k T x + w k 0 (4.7) y_{k}(\boldsymbol{x})=\boldsymbol{w}_{k}^{T}\boldsymbol{x}+w_{k0}\tag{4.7} yk(x)=wkTx+wk0(4.7)
对于点 x \boldsymbol{x} x ,如果对于所有的 j ≠ k j \ne k j=k 都 有 y k ( x ) > y j ( x ) y_{k}(\boldsymbol{x})\gt y_{j}(\boldsymbol{x}) yk(x)>yj(x) ,那么就把它分到 C k \mathcal{C}_k Ck 。 于是类别 C k \mathcal{C}_k Ck 和 C j \mathcal{C}_j Cj 之间的决策⾯为 y k ( x ) = y j ( x ) y_{k}(\boldsymbol{x})=y_{j}(\boldsymbol{x}) yk(x)=yj(x),并且对应于⼀个 ( D − 1 ) (D − 1) (D−1) 维超平⾯,形式为
( w k − w j ) T x + ( w k 0 − w j 0 ) = 0 (4.8) (\boldsymbol{w}_{k}-\boldsymbol{w}_{j})^{T}\boldsymbol{x}+(w_{k0}-w_{j0})=0\tag{4.8} (wk−wj)Tx+(wk0−wj0)=0(4.8)
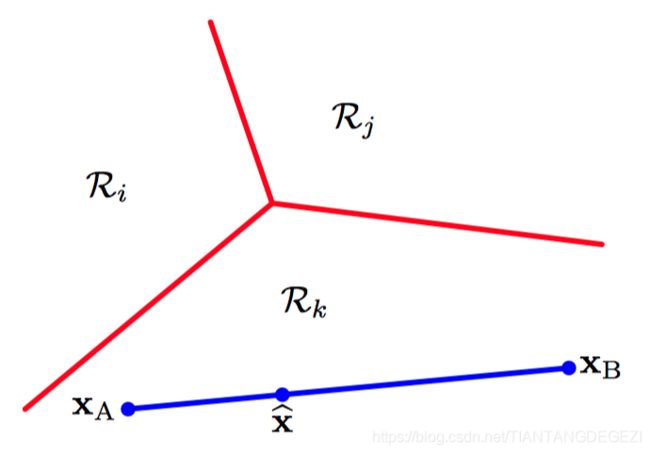
考虑两个点 x A \boldsymbol{x}_A xA 和 x B \boldsymbol{x}_B xB ,两个点都位于决策区域 R k \mathcal{R}_k Rk 中, 任何位于连接 x A \boldsymbol{x}_A xA 和 x B \boldsymbol{x}_B xB 的线段上的点都可以表⽰成下⾯的形式
x ^ = λ x A + ( 1 − λ ) x B (4.9) \hat{\boldsymbol{x}}=\lambda \boldsymbol{x}_{A}+(1-\lambda)\boldsymbol{x}_{B}\tag{4.9} x^=λxA+(1−λ)xB(4.9)
其中, 0 ≤ λ ≤ 1 0\le\lambda\le1 0≤λ≤1 。根据判别函数的线性性质,有
y k ( x ^ ) = λ y k ( x A ) + ( 1 − λ ) y k ( x B ) (4.10) y_{k}(\hat{\boldsymbol{x}})=\lambda y_{k}(\boldsymbol{x}_{A})+(1-\lambda)y_{k}(\boldsymbol{x}_{B})\tag{4.10} yk(x^)=λyk(xA)+(1−λ)yk(xB)(4.10)
由于 x A \boldsymbol{x}_A xA 和 x B \boldsymbol{x}_B xB 位于 R k \mathcal{R}_k Rk 内部,因此对于所有 j ≠ k j \ne k j=k , 都有 y k ( x A ) > y j ( x A ) y_{k}(\boldsymbol{x}_{A})\gt y_{j}(\boldsymbol{x}_{A}) yk(xA)>yj(xA) 以及 y k ( x B ) > y j ( x B ) y_{k}(\boldsymbol{x}_{B})\gt y_{j}(\boldsymbol{x}_{B}) yk(xB)>yj(xB) ,因此 y k ( x ^ ) > y j ( x ^ ) y_{k}(\hat{\boldsymbol{x}})\gt y_{j}(\hat{\boldsymbol{x}}) yk(x^)>yj(x^) ,从⽽ x ^ \hat{\boldsymbol{x}} x^ 也位于 R k \mathcal{R}_k Rk 内部,即 R k \mathcal{R}_k Rk 是单连通的并且是凸的。
如图4.3,多类判别函数的决策区域的说明, 决策边界⽤红⾊表⽰。
3,⽤于分类的最⼩平⽅⽅法
每个类别 C k \mathcal{C}_k Ck 由⾃⼰的线性模型描述,即公式(4.7),其中 k = 1 , … , K k = 1, \dots , K k=1,…,K 。使⽤向量记号表⽰,即
y ( x ) = W ~ T x ~ (4.11) \boldsymbol{y}(\boldsymbol{x})=\tilde{\boldsymbol{W}}^{T}\tilde{\boldsymbol{x}}\tag{4.11} y(x)=W~Tx~(4.11)
其中 W ~ \tilde{\boldsymbol{W}} W~ 是⼀个矩阵,第 k k k 列由 D + 1 D + 1 D+1 维向量 w ~ k = ( w k 0 , w k T ) T \tilde{\boldsymbol{w}}_k=(w_{k0},w_{k}^{T})^{T} w~k=(wk0,wkT)T 组成, x ~ \tilde{\boldsymbol{x}} x~ 是对应的增⼴输⼊向量 ( 1 , x T ) T (1, \boldsymbol{x}^{T})^{T} (1,xT)T, 它带有⼀个虚输⼊ x 0 = 1 x_0 = 1 x0=1 。
现在通过最⼩化平⽅和误差函数来确定参数矩阵 W ~ \tilde{\boldsymbol{W}} W~ ,考虑⼀个训练数据集 { x n , t n } \{\boldsymbol{x}_n, \boldsymbol{t}_n\} {xn,tn},其中 $n = 1,\dots , N $,然后定义⼀个矩阵 T \boldsymbol{T} T ,它的第 n n n ⾏是向量 t n T \boldsymbol{t}_{n}^{T} tnT ,定义⼀个矩阵 X ~ \tilde{\boldsymbol{X}} X~ ,它的第 n n n ⾏是 x ~ n T \tilde{\boldsymbol{x}}_{n}^{T} x~nT 。这样,平⽅和误差函数可以写成
E D ( W ~ ) = 1 2 Tr { ( X ~ W ~ − T ) T ( X ~ W ~ − T ) } (4.12) E_{D}(\tilde{\boldsymbol{W}})=\frac{1}{2}\text{Tr}\{(\tilde{\boldsymbol{X}}\tilde{\boldsymbol{W}}-\boldsymbol{T})^{T}(\tilde{\boldsymbol{X}}\tilde{\boldsymbol{W}}-\boldsymbol{T})\}\tag{4.12} ED(W~)=21Tr{(X~W~−T)T(X~W~−T)}(4.12)
令关于 W ~ \tilde{\boldsymbol{W}} W~ 的导数等于零,整理,可以得到 W ~ \tilde{\boldsymbol{W}} W~ 的解,形式为
W ~ = ( X ~ T W ~ ) − 1 X ~ T T = X ~ † T (4.13) \tilde{\boldsymbol{W}}=(\tilde{\boldsymbol{X}}^{T}\tilde{\boldsymbol{W}})^{-1}\tilde{\boldsymbol{X}}^{T}\boldsymbol{T}=\tilde{\boldsymbol{X}}^{\dagger}\boldsymbol{T}\tag{4.13} W~=(X~TW~)−1X~TT=X~†T(4.13)
其中 X ~ † \tilde{\boldsymbol{X}}^{\dagger} X~† 是矩阵 X ~ \tilde{\boldsymbol{X}} X~ 的伪逆矩阵。即得判别函数,形式为
y ( x ) = W ~ T x ~ = T T ( X ~ † ) T x ~ (4.14) y(\boldsymbol{x})=\tilde{\boldsymbol{W}}^{T}\tilde{\boldsymbol{x}}=\boldsymbol{T}^{T}(\tilde{\boldsymbol{X}}^{\dagger})^{T}\tilde{\boldsymbol{x}}\tag{4.14} y(x)=W~Tx~=TT(X~†)Tx~(4.14)
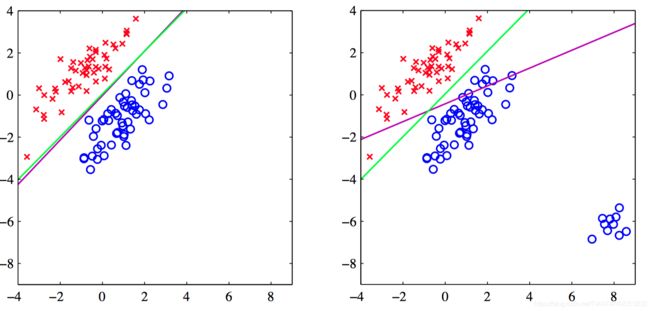
如图4.4,左图给出了来⾃两个类别的数据,⽤红⾊叉形和蓝⾊圆圈表⽰。同时给出的还有通过最⼩平⽅⽅法找到的决策边界(洋红⾊曲线)以及logistic回归模型给出的决策边界(绿⾊曲线);右图给出了当额外的数据点被添加到左图的底部之后得到的结果,这表明最⼩平⽅⽅法对于异常点很敏感,这与logistic回归不同。
多⽬标变量的最⼩平⽅解的⼀个重要的性质是:如果训练集⾥的每个⽬标向量都满⾜某个线性限制
a T t n + b = 0 (4.15) \boldsymbol{a}^{T}\boldsymbol{t}_{n}+b=0\tag{4.15} aTtn+b=0(4.15)
其中 a \boldsymbol{a} a 和 b b b 为常量,那么对于任何 x \boldsymbol{x} x 值,模型的预测也满⾜同样的限制,即
a T y ( x ) + b = 0 (4.16) \boldsymbol{a}^{T}\boldsymbol{y}(\boldsymbol{x})+b=0\tag{4.16} aTy(x)+b=0(4.16)
因此如果使⽤ K K K 分类的“1-of-K ”表达⽅式,那么这个模型做出的预测会具有下⾯的性质:对于任意的 x \boldsymbol{x} x 的值, y ( x ) \boldsymbol{y}(\boldsymbol{x}) y(x) 的元素的和等于1。
举例,由三个类别组成的⼈⼯数据集,训练数据点分别⽤红⾊(×)、绿⾊(+)、蓝⾊(◦)标出。 直线表⽰决策边界, 背景颜⾊表⽰决策区域代表的类别。
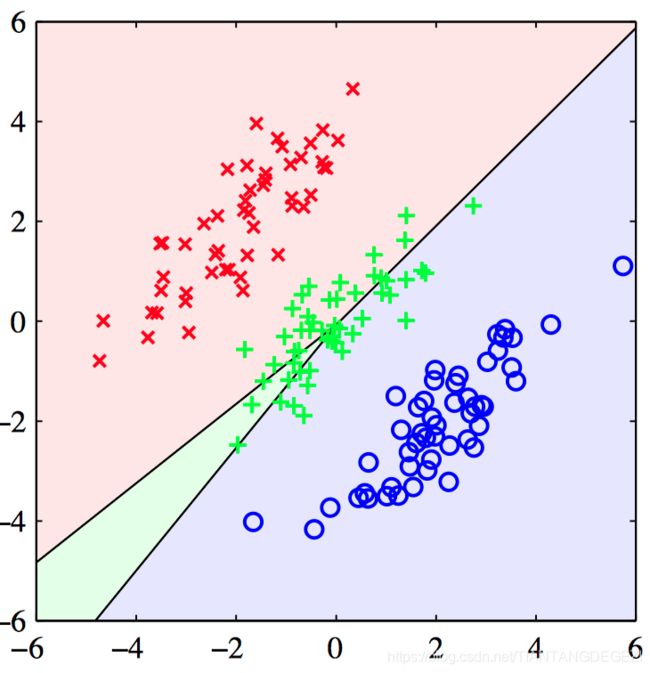
如图4.5,使⽤最⼩平⽅判别函数,分配到绿⾊类别的输⼊空间的区域过⼩,⼤部分来⾃这个类别的点都被错误分类。
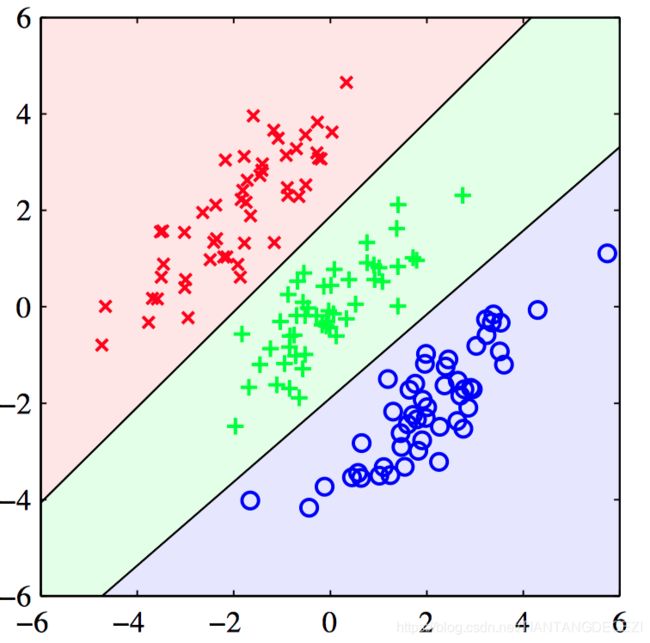
如图4.6,使⽤logistic回归的结果,给出了训练数据的正确分类情况。
4,Fisher线性判别函数
假设有⼀个 D D D 维输⼊向量 x \boldsymbol{x} x ,然后使⽤下式投影到⼀维
y = w T x (4.17) y=\boldsymbol{w}^{T}\boldsymbol{x}\tag{4.17} y=wTx(4.17)
如果在 y y y 上设置⼀个阈值,然后把 y ≥ − w 0 y\ge -w_0 y≥−w0 的样本分为 C 1 \mathcal{C}_1 C1 类,把其余的样本分为 C 2 \mathcal{C}_2 C2 类,那么就得到了一个标准的线性分类器。
考虑⼀个⼆分类问题,这个问题中有 C 1 \mathcal{C}_1 C1 类的 N 1 N_1 N1 个点以及 C 2 \mathcal{C}_2 C2 类的 N 2 N_2 N2 个点。因此两类的均值向量为
m 1 = 1 N 1 ∑ n ∈ C 1 x n m 2 = 1 N 2 ∑ n ∈ C 2 x n \boldsymbol{m}_{1}=\frac{1}{N_1}\sum_{n\in\mathcal{C_1}}\boldsymbol{x}_{n}\\ \boldsymbol{m}_{2}=\frac{1}{N_2}\sum_{n\in\mathcal{C_2}}\boldsymbol{x}_{n} m1=N11n∈C1∑xnm2=N21n∈C2∑xn
如果投影到 w \boldsymbol{w} w 上,那么最简单的度量类别之间分开程度的⽅式就是类别均值投影之后的距离。这说明可以选择 w \boldsymbol{w} w 使得下式取得最⼤值
m 2 − m 1 = w T ( m 2 − m 1 ) (4.18) m_2-m_1=\boldsymbol{w}^{T}(\boldsymbol{m}_2-\boldsymbol{m}_1)\tag{4.18} m2−m1=wT(m2−m1)(4.18)
其中,
m k = w T m k m_k=\boldsymbol{w}^{T}\boldsymbol{m}_{k} mk=wTmk
是来⾃类别 C k \mathcal{C}_k Ck 的投影数据的均值。
如图4.7,左图给出了来⾃两个类别(表⽰为红⾊和蓝⾊)的样本,以及在连接两个类别的均值的直线上的投影的直⽅图。注意,在投影空间中,存在⼀个⽐较严重的类别重叠。右图给出的基于Fisher线性判别准则的对应投影,表明了类别切分的效果得到了极⼤的提升。
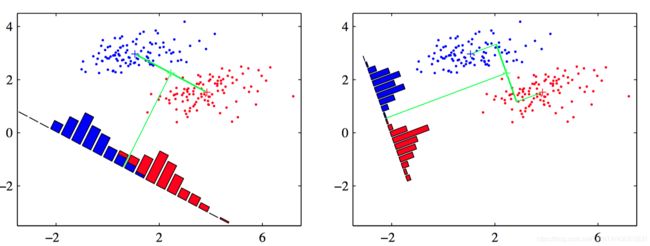
Fisher提出的思想是最⼤化⼀个函数,这个函数能够让类均值的投影分开得较⼤,同时让每个类别内部的⽅差较⼩,从⽽最⼩化了类别的重叠。
投影公式(4.17)将 x \boldsymbol{x} x 的⼀组有标记的数据点变换为⼀位空间 y y y 的⼀组有标记数据点。来⾃类别 C k \mathcal{C}_k Ck 的数据经过变换后的类内⽅差为
s k 2 = ∑ n ∈ C k ( y n − m k ) 2 (4.19) s_{k}^{2}=\sum_{n\in \mathcal{C}_k}(y_n-m_k)^{2}\tag{4.19} sk2=n∈Ck∑(yn−mk)2(4.19)
其中, y n = w T x n y_n=\boldsymbol{w}^{T}\boldsymbol{x}_{n} yn=wTxn 。把整个数据集的总的类内⽅差定义为 s 1 2 + s 2 2 s_1^2+s_2^2 s12+s22 ,Fisher准则 根据类间⽅差和类内⽅差的⽐值定义,即
J ( w ) = ( m 2 − m 1 ) 2 s 1 2 + s 2 2 (4.20) J(\boldsymbol{w})=\frac{(m_2-m_1)^{2}}{s_1^2+s_2^2}\tag{4.20} J(w)=s12+s22(m2−m1)2(4.20)
不难推导, J ( w ) J(\boldsymbol{w}) J(w) 对 w \boldsymbol{w} w 的依赖
J ( w ) = w T S B w w T S W w (4.21) J(\boldsymbol{w})=\frac{\boldsymbol{w}^{T}\boldsymbol{S}_B\boldsymbol{w}}{\boldsymbol{w}^{T}\boldsymbol{S}_W\boldsymbol{w}}\tag{4.21} J(w)=wTSWwwTSBw(4.21)
其中 S B \boldsymbol{S}_B SB 是类间(between-class)协⽅差矩阵,形式为
S B = ( m 2 − m 1 ) ( m 2 − m 1 ) T \boldsymbol{S}_B=(\boldsymbol{m}_2-\boldsymbol{m}_1)(\boldsymbol{m}_2-\boldsymbol{m}_1)^{T} SB=(m2−m1)(m2−m1)T
S W \boldsymbol{S}_W SW 被称为类内(within-class)协⽅差矩阵,形式为
S W = ∑ n ∈ C 1 ( x n − m 1 ) ( x n − m 1 ) T + ∑ n ∈ C 2 ( x n − m 2 ) ( x n − m 2 ) T \boldsymbol{S}_W=\sum_{n\in \mathcal{C}_1}(\boldsymbol{x}_n-\boldsymbol{m}_1)(\boldsymbol{x}_n-\boldsymbol{m}_1)^{T}+\sum_{n\in \mathcal{C}_2}(\boldsymbol{x}_n-\boldsymbol{m}_2)(\boldsymbol{x}_n-\boldsymbol{m}_2)^{T} SW=n∈C1∑(xn−m1)(xn−m1)T+n∈C2∑(xn−m2)(xn−m2)T
对公式(4.21)关于 w \boldsymbol{w} w 求导,发现 J ( w ) J(\boldsymbol{w}) J(w) 取得最⼤值的条件为
( w T S B w ) S W w = ( w T S W w ) S B w (4.22) (\boldsymbol{w}^{T}\boldsymbol{S}_B\boldsymbol{w})\boldsymbol{S}_W\boldsymbol{w}=(\boldsymbol{w}^{T}\boldsymbol{S}_W\boldsymbol{w})\boldsymbol{S}_B\boldsymbol{w}\tag{4.22} (wTSBw)SWw=(wTSWw)SBw(4.22)
可以发现, S B w \boldsymbol{S}_B\boldsymbol{w} SBw 总是在 ( m 2 − m 1 ) (\boldsymbol{m}_2−\boldsymbol{m}_1) (m2−m1) 的⽅向上。 更重要的是, 若不关⼼ w \boldsymbol{w} w 的⼤⼩, 只关⼼它的⽅向, 因此可以忽略标量因⼦ ( w T S B w ) (\boldsymbol{w}^{T}\boldsymbol{S}_B\boldsymbol{w}) (wTSBw) 和 ( w T S W w ) (\boldsymbol{w}^{T}\boldsymbol{S}_W\boldsymbol{w}) (wTSWw) 。 将公式(4.22)的两侧乘以 S W − 1 \boldsymbol{S}_{W}^{-1} SW−1 ,即得 Fisher线性判别函数(Fisher linear discriminant)
w ∝ S W − 1 ( m 2 − m 1 ) (4.23) \boldsymbol{w}\propto \boldsymbol{S}_{W}^{-1}(\boldsymbol{m}_2-\boldsymbol{m}_1)\tag{4.23} w∝SW−1(m2−m1)(4.23)
如果类内协⽅差矩阵是各向同性的,从⽽ S W \boldsymbol{S}_W SW 正⽐于单位矩阵,那么我们看到 w \boldsymbol{w} w 正⽐于类均值的差。
构建 Fisher线性判别函数 ,其⽅法为:选择⼀个阈值 y 0 y_0 y0 ,使得当 y ( x ) ≥ y 0 y(\boldsymbol{x})\ge y_0 y(x)≥y0 时,把数据点分到 C 1 \mathcal{C}_1 C1 ,否则把数据点分到 C 2 \mathcal{C}_2 C2 。
5,与最⼩平⽅的关系
最⼩平⽅⽅法确定线性判别函数的⽬标是使模型的预测尽可能地与⽬标值接近。相反, Fisher判别准则 的⽬标是使输出空间的类别有最⼤的区分度。
对于⼆分类问题,Fisher准则可以看成最⼩平⽅的⼀个特例。作如下假设:让属于 C 1 \mathcal{C}_1 C1 的⽬标值等于 N N 1 \frac{N}{N_1} N1N ,其中 N 1 N_1 N1 是类别 C 1 \mathcal{C}_1 C1 的模式的数量, N N N 是总的模式数量。这个⽬标值近似于类别 C 1 \mathcal{C}_1 C1 的先验概率的导数。 对于类别 C 2 \mathcal{C}_2 C2 , 令⽬标值等于 − N N 2 −\frac{N}{N_2} −N2N , 其中 N 2 N_2 N2 是类别 C 2 \mathcal{C}_2 C2 的模式的数量。平⽅和误差函数可以写成
E = 1 2 ∑ n = 1 N ( w T x n + w 0 − t n ) 2 (4.24) E=\frac{1}{2}\sum_{n=1}^{N}(\boldsymbol{w}^{T}\boldsymbol{x}_{n}+w_0-t_n)^{2}\tag{4.24} E=21n=1∑N(wTxn+w0−tn)2(4.24)
令 E E E 关于 w 0 w_0 w0 和 w \boldsymbol{w} w 的导数等于零,使⽤对于⽬标值 t n t_n tn 的表⽰⽅法,可以得到偏置的表达式
w 0 = − w T m (4.25) w_0=-\boldsymbol{w}^{T}\boldsymbol{m}\tag{4.25} w0=−wTm(4.25)
其中,
∑ n = 1 N t n = N 1 N N 1 − N 2 N N 2 = 0 m = 1 N ∑ n = 1 N x n = 1 N ( N 1 m 1 + N 2 m 2 ) \sum_{n=1}^{N}t_n=N_1\frac{N}{N_1}-N_2\frac{N}{N_2}=0\\ \boldsymbol{m}=\frac{1}{N}\sum_{n=1}^{N}\boldsymbol{x}_n=\frac{1}{N}(N_1\boldsymbol{m}_1+N_2\boldsymbol{m}_2) n=1∑Ntn=N1N1N−N2N2N=0m=N1n=1∑Nxn=N1(N1m1+N2m2)
使⽤对于 t n t_n tn 的新的表⽰⽅法可得
( S W + N 1 N 2 N S B ) w = N ( m 1 − m 2 ) (4.26) \left(\boldsymbol{S}_W+\frac{N_1N_2}{N}\boldsymbol{S}_B\right)\boldsymbol{w}=N(\boldsymbol{m_1}-\boldsymbol{m}_2)\tag{4.26} (SW+NN1N2SB)w=N(m1−m2)(4.26)
由此可见,可以推导出公式(4.23),即权向量恰好与根据Fisher判别准则得到的结果相同。
6,多分类的Fisher判别函数
现在考虑Fisher判别函数对于 K > 2 K>2 K>2 个类别的推⼴。 假设输⼊空间的维度 D D D ⼤于类别数量 K K K ,引⼊ D ′ > 1 D^{\prime} > 1 D′>1 个线性“特征” y k = w k T x y_k = \boldsymbol{w}_k^{T}\boldsymbol{x} yk=wkTx ,其中 k = 1 , … , D ′ k=1,\dots,D^{\prime} k=1,…,D′ 。 为了⽅便, 这些特征值可以聚集起来组成向量 y \boldsymbol{y} y ,类似地,权向量 { w k } \{\boldsymbol{w}_k\} {wk} 可以被看成矩阵 W \boldsymbol{W} W 的列。因此
y = W T x (4.27) \boldsymbol{y}=\boldsymbol{W}^{T}\boldsymbol{x}\tag{4.27} y=WTx(4.27)
类内协⽅差矩阵推⼴到 K K K 类,有
S W = ∑ k = 1 K S k (4.28) \boldsymbol{S}_{W}=\sum_{k=1}^{K}\boldsymbol{S}_{k}\tag{4.28} SW=k=1∑KSk(4.28)
其中,
S k = ∑ n ∈ C k ( x n − m k ) ( x n − m k ) T m k = 1 N k ∑ n ∈ C k x n \boldsymbol{S}_{k}=\sum_{n\in \mathcal{C}_k}(\boldsymbol{x}_n-\boldsymbol{m}_k)(\boldsymbol{x}_n-\boldsymbol{m}_k)^{T}\\ \boldsymbol{m}_{k}=\frac{1}{N_k}\sum_{n\in\mathcal{C_k}}\boldsymbol{x}_{n} Sk=n∈Ck∑(xn−mk)(xn−mk)Tmk=Nk1n∈Ck∑xn
其中 N k N_k Nk 是类别 C k \mathcal{C}_k Ck 中模式的数量。
为了找到类间协⽅差矩阵的推⼴,使⽤Duda and Hart(1973)的⽅法,⾸先考虑整体的协⽅差矩阵
S T = ∑ n = 1 N ( x n − m ) ( x n − m ) T (4.29) \boldsymbol{S}_{T}=\sum_{n=1}^{N}(\boldsymbol{x}_n-\boldsymbol{m})(\boldsymbol{x}_n-\boldsymbol{m})^{T}\tag{4.29} ST=n=1∑N(xn−m)(xn−m)T(4.29)
其中 m \boldsymbol{m} m 是全体数据的均值
m = 1 N ∑ n = 1 N x n = 1 N ∑ k = 1 K N k m k \boldsymbol{m}=\frac{1}{N}\sum_{n=1}^{N}\boldsymbol{x}_{n}=\frac{1}{N}\sum_{k=1}^{K}N_k\boldsymbol{m}_{k} m=N1n=1∑Nxn=N1k=1∑KNkmk
其中 N = ∑ k N k N = \sum_{k} N_k N=∑kNk 是数据点的总数。
整体的协⽅差矩阵可以分解为公式(4.28)给出的类内协⽅差矩阵,加上另⼀个矩阵 S B \boldsymbol{S}_B SB ,它可以看做类间协⽅差矩阵。
S T = S W + S B (4.30) \boldsymbol{S}_{T}=\boldsymbol{S}_{W}+\boldsymbol{S}_{B}\tag{4.30} ST=SW+SB(4.30)
其中,
S B = ∑ k = 1 K N k ( m k − m ) ( m k − m ) T \boldsymbol{S}_B=\sum_{k=1}^{K}N_k(\boldsymbol{m}_k-\boldsymbol{m})(\boldsymbol{m}_k-\boldsymbol{m})^{T} SB=k=1∑KNk(mk−m)(mk−m)T
协⽅差矩阵被定义在原始的 x \boldsymbol{x} x 空间中。现在在投影的 D ′ D^{\prime} D′ 维 y \boldsymbol{y} y 空间中定义类似的矩阵
S W = ∑ k = 1 K ∑ n ∈ C k ( y n − μ k ) ( y n − μ k ) T S B = ∑ k = 1 K N k ( μ k − μ ) ( μ k − μ ) T \boldsymbol{S}_{W}=\sum_{k=1}^{K}\sum_{n\in \mathcal{C}_k}(\boldsymbol{y}_n-\boldsymbol{\mu}_k)(\boldsymbol{y}_n-\boldsymbol{\mu}_k)^{T}\\ \boldsymbol{S}_B=\sum_{k=1}^{K}N_k(\boldsymbol{\mu}_k-\boldsymbol{\mu})(\boldsymbol{\mu}_k-\boldsymbol{\mu})^{T} SW=k=1∑Kn∈Ck∑(yn−μk)(yn−μk)TSB=k=1∑KNk(μk−μ)(μk−μ)T
其中,
μ k = 1 N k ∑ n ∈ C k y n μ = 1 N ∑ k = 1 K N k μ k \boldsymbol{\mu}_k=\frac{1}{N_k}\sum_{n\in \mathcal{C}_k}\boldsymbol{y}_n\\ \boldsymbol{\mu}=\frac{1}{N}\sum_{k=1}^{K}N_k\boldsymbol{\mu}_k μk=Nk1n∈Ck∑ynμ=N1k=1∑KNkμk
我们想构造⼀个标量,当类间协⽅差较⼤且类内协⽅差较⼩时,这个标量会较⼤。有许多可能的准则选择⽅式(Fukunaga, 1990)。其中⼀种选择是
J ( W ) = Tr { s W − 1 s B } (4.31) J(\boldsymbol{W})=\text{Tr}\{\boldsymbol{s}_{W}^{-1}\boldsymbol{s}_{B}\}\tag{4.31} J(W)=Tr{sW−1sB}(4.31)
这个判别准则可以显式地写成投影矩阵 W \boldsymbol{W} W 的函数,形式为
J ( W ) = Tr { ( W T S W W ) − 1 ( W T S B W ) } (4.32) J(\boldsymbol{W})=\text{Tr}\{(\boldsymbol{W}^{T}\boldsymbol{S}_{W}\boldsymbol{W})^{-1}(\boldsymbol{W}^{T}\boldsymbol{S}_{B}\boldsymbol{W})\}\tag{4.32} J(W)=Tr{(WTSWW)−1(WTSBW)}(4.32)
7,感知器算法
线性判别模型的另⼀个例⼦是Rosenblatt(1962)提出的感知器算法。对应于⼀个⼆分类的模型,输⼊向量 x \boldsymbol{x} x ⾸先使⽤⼀个固定的⾮线性变换得到⼀个特征向量 ϕ ( x ) \boldsymbol{\phi}(\boldsymbol{x}) ϕ(x) , 这个特征向量然后被⽤于构造⼀个⼀般的线性模型,形式为
y ( x ) = f ( w T ϕ ( x ) ) (4.33) y(\boldsymbol{x})=f(\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}))\tag{4.33} y(x)=f(wTϕ(x))(4.33)
其中⾮线性激活函数 f ( ⋅ ) f(·) f(⋅) 是⼀个阶梯函数,形式为
f ( a ) = { + 1 , a ≥ 0 − 1 , a < 0 f(a)=\begin{cases}+1,&a\ge 0\\ -1,&a<0\end{cases} f(a)={+1,−1,a≥0a<0
向量 ϕ ( x ) \boldsymbol{\phi}(\boldsymbol{x}) ϕ(x) 通常包含⼀个偏置分量 ϕ 0 ( x ) = 0 \phi_{0}(\boldsymbol{x})=0 ϕ0(x)=0 。对于感知器,使⽤ t = + 1 t=+1 t=+1 表⽰ C 1 \mathcal{C}_1 C1 ,使⽤ t = − 1 t=−1 t=−1 表⽰ C 2 \mathcal{C}_2 C2 ,这与激活函数的选择相匹配。
为了推导误差函数,即感知器准则(perceptron criterion), 注意到我们正在做的是寻找⼀个权向量 w \boldsymbol{w} w 使得对于类别 C 1 \mathcal{C}_1 C1 中的模式 x n \boldsymbol{x}_n xn 都有 w T ϕ ( x n ) > 0 \boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)>0 wTϕ(xn)>0 , ⽽对于类别 C 2 \mathcal{C}_2 C2 中的模式 x n \boldsymbol{x}_n xn 都有 w T ϕ ( x n ) < 0 \boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)<0 wTϕ(xn)<0 。 使⽤ t ∈ { − 1 , + 1 } t \in\{−1, +1\} t∈{−1,+1} 这种⽬标变量的表⽰⽅法,要做的就是使得所有的模式都满⾜ w T ϕ ( x n ) t n > 0 \boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)t_{n}>0 wTϕ(xn)tn>0 。 对于正确分类的模式,感知器准则赋予零误差,⽽对于误分类的模式 x n \boldsymbol{x}_n xn ,它试着最⼩化 − w T ϕ ( x n ) t n -\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)t_{n} −wTϕ(xn)tn 。因此,感知器准则为
E P ( w ) = − ∑ n ∈ M w T ϕ n t n (4.34) E_{P}(\boldsymbol{w})=-\sum_{n\in\mathcal{M}}\boldsymbol{w}^{T}\boldsymbol{\phi}_nt_{n}\tag{4.34} EP(w)=−n∈M∑wTϕntn(4.34)
其中 ϕ n = ϕ ( x n ) \boldsymbol{\phi}_n=\boldsymbol{\phi}(\boldsymbol{x}_n) ϕn=ϕ(xn) 和 M \mathcal{M} M 表⽰所有误分类模式的集合。某个特定的误分类模式对于误差函数的贡献是 w \boldsymbol{w} w 空间中模式被误分类的区域中 w \boldsymbol{w} w 的线性函数, ⽽在正确分类的区域,误差函数等于零。 总的误差函数因此是分段线性的。
现在对这个误差函数使⽤随机梯度下降算法。这样,权向量 w \boldsymbol{w} w 的变化为
w ( τ + 1 ) = w ( τ ) − η ∇ E P ( w ) = w ( τ ) + η ϕ n t n (4.35) \begin{aligned}\boldsymbol{w}^{(\tau+1)}&=\boldsymbol{w}^{(\tau)}-\eta\nabla E_{P}(\boldsymbol{w})\\&=\boldsymbol{w}^{(\tau)}+\eta\boldsymbol{\phi}_{n}t_n\end{aligned}\tag{4.35} w(τ+1)=w(τ)−η∇EP(w)=w(τ)+ηϕntn(4.35)
其中 η \eta η 是学习率参数, τ \tau τ 是⼀个整数,是算法运⾏次数的索引。
感知器学习算法可以简单地表⽰如下:我们反复对于训练模式进⾏循环处理,对于每个模式 x n \boldsymbol{x}_n xn 计算感知器函数(4.33)。如果模式正确分类,那么权向量保持不变,⽽如果模式被错误分类,那么对于类别 C 1 \mathcal{C}_1 C1 , 我们把向量 ϕ ( x n ) \boldsymbol{\phi}(\boldsymbol{x}_n) ϕ(xn) 加到当前对于权向量 w \boldsymbol{w} w 的估计值上,⽽对于类别 C 2 \mathcal{C}_2 C2 ,我们从 w \boldsymbol{w} w 中减掉向量 ϕ ( x n ) \boldsymbol{\phi}(\boldsymbol{x}_n) ϕ(xn)。
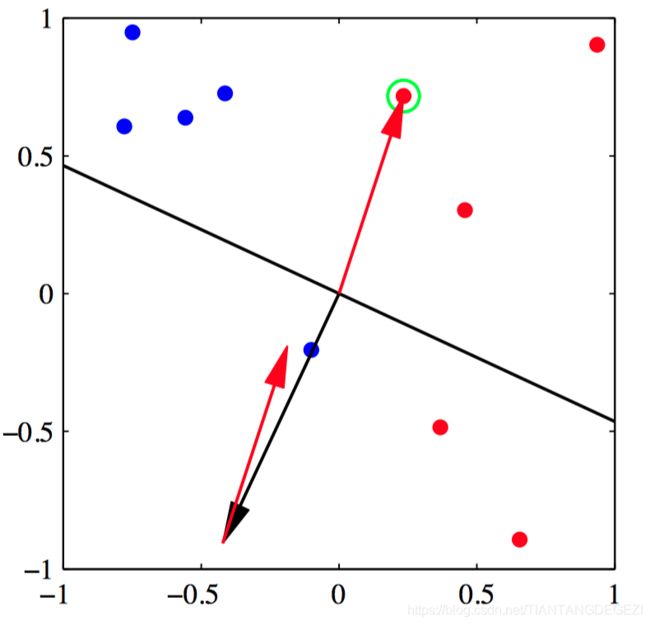
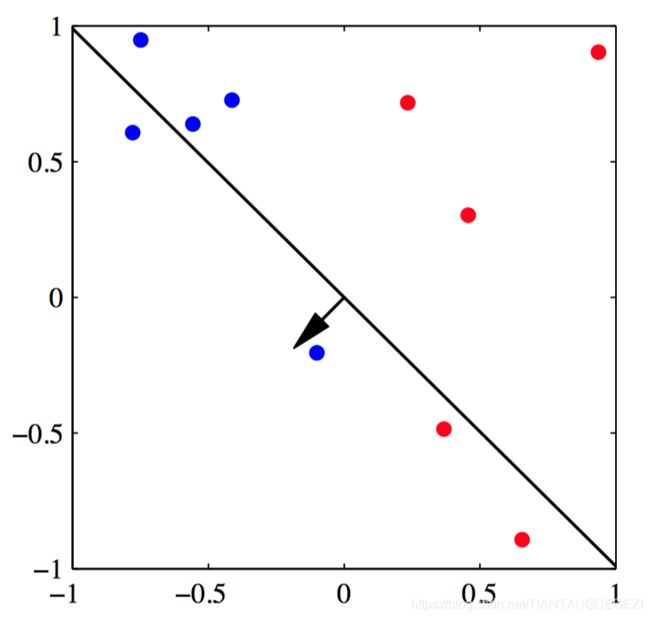
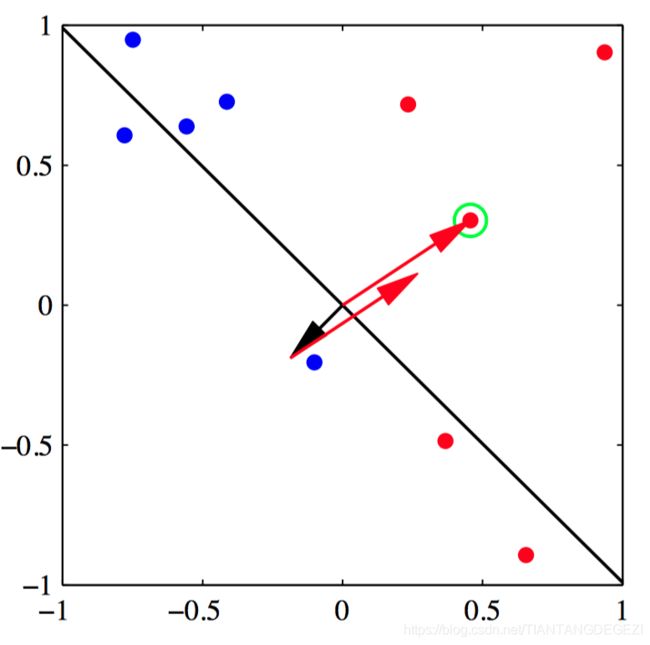
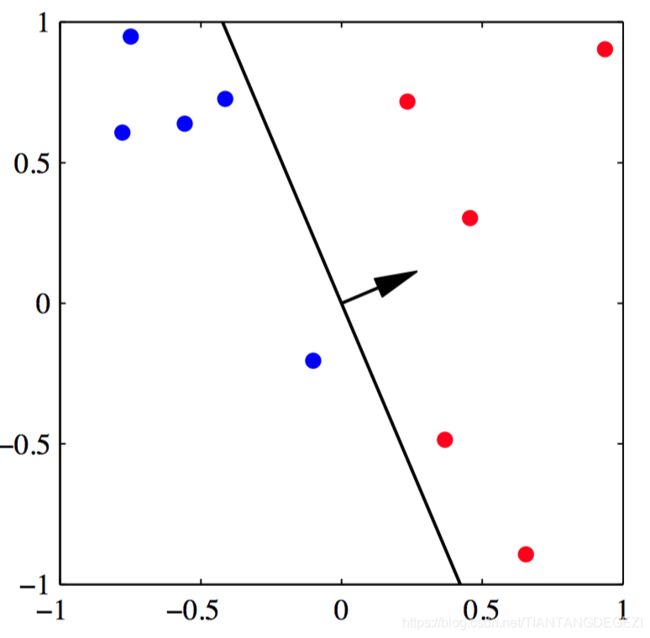
如图4.8~4.11,感知器算法收敛性的说明, 给出了⼆维特征空间 ( ϕ 1 , ϕ 2 ) (\phi_1,\phi_2) (ϕ1,ϕ2) 中的来⾃两个类别的数据点(红⾊和蓝 ⾊)。图4.8给出了初始参数向量 w \boldsymbol{w} w ,表⽰为⿊⾊箭头,以及对应的决策边界(⿊⾊直线),其中箭头指向被分类为红⾊类别的决策区域。⽤绿⾊圆圈标出的数据点被误分类,因此它的特征向量被加到当前的权向量中,给出了新的决策边界,如图4.9所⽰。 图4.10给出了下⼀个误分类的点,⽤绿⾊圆圈标出,它的特征向量再次被加到权向量上,给出了图4.11的决策边界。这个边界中所有的数据点都被正确分类。