【SPSS】包含多元线性回归、聚类分析、判别分析、主成分、相关系数、非参数秩检验的spss使用方法，含有相关例题，可以解决“数学建模”中数据建模的大部分问题

记录《多元统计分析》关于spss软件的使用，本篇教程不涉及具体模型的推导，通过例题来带领大家入门spss软件，学习软件基本的使用，解决常见数模问题。

本篇所有数据都可以在百度网盘上下载：
链接：https://pan.baidu.com/s/1-yfF2pzf38fQRcq3zF2SJw?pwd=abcd
提取码：abcd

---

一、多元线性回归

1.1 提出问题

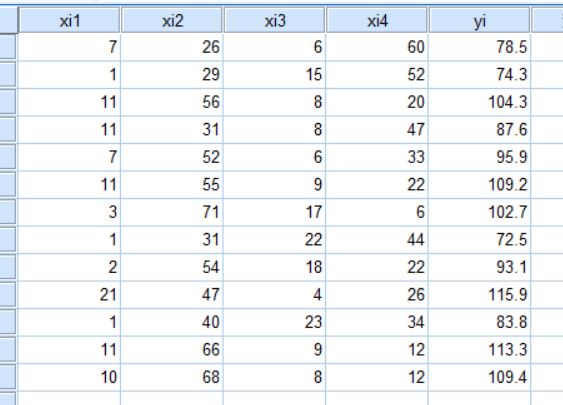
1.2 数据格式

1.3 SPSS操作

在数据编辑器中打开数据集“水泥成分.sav”， 在“分析”主菜单中用鼠标指向“线性”选项，然后在打开的子菜单中单击“线性”选项，打开“线性回归”对话框，在“因变量”输入框输入变量名“yi”，在“自变量”输入框输入变量名“xi1”、“xi2”、“xi3”、“xi4”。点击“选项”按钮，打开“线性回归:选项”对话框，在“步进法条件”方框中选择“使用F值”单选按钮，在“进入”输入框输入数值4，在“除去” 输入框输入数值3.8。其它选项按默认设置。

下面选择不同的多元分析方法进行分析。

1.3.1 全回归（输入）——所有的自变量进入回归方程

在“线性回归:选项”对话框中选择“方法”下拉式列表框中的“输入”选项，将用全回归方法进行多元回归，结果如下：
➡️变量输入输出表

表中第二列为输入的变量，第三列为剔除的变量，第四列表示采用的方法是全回归法。本例中，四个变量全部用做输入变量，没有变量被剔除。

➡️模型综述表

表中列出了相关系数（R）、相关系数的平方（R Square）、调整的相关系数的平方（Adjusted R Square）、估计值的标准误差（Std. Error of Estimate）。本例中，相关系数等于0.991，说明自变量和因变量之间有较好的相关性。R Square等于0.982，表示这四个变量一起可以解释因变量98.2%的变异性。

➡️方差分析表

由于显著性概率小于5%，所以拒绝原假设，即认为回归系数不为0，回归方程有意义。

➡️系数分析表

该表列出了各个自变量和常数项的非标准化系数（Unstandardized Coefficients）（包括变量X的待定系数（B）、常数项取值（B）及标准误差（Std. Error））、标准化系数（Standardized Coefficients）（Beta值）、t值、显著性水平（Sig.）。

本例中，用全回归法得到多元回归方程式为：
yi=62.405+1.551xi1+0.510xi2+0.102xi3-0.144xi4
模型的相关系数为0.991。

1.3.2 逐步回归法（步进法）——“有进有出法”，应用广泛

在“线性回归:选项”对话框中选择“方法”下拉式列表框中的“步进”选项，将用逐步回归法进行多元回归，结果如下：
➡️变量输入输出表

表中给出了每一步进入方程式的变量和剔除的变量，以及采用的多元回归方法和相应的准则。本例中，回归共分4步完成，前3步先后输入变量xi4 、xi1和 xi2，第4步剔除变量xi4，采用的准则是：F≥4.000时，对应变量进入方程式，F≤3.800时，变量被剔除。最后只剩下变量xi1和 xi2。

➡️模型综述表

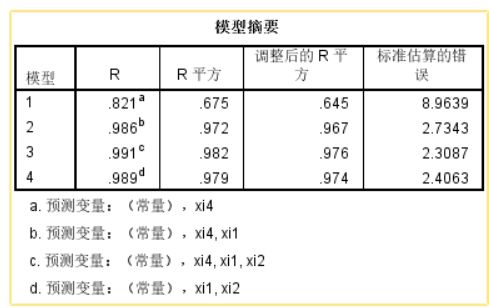
表中列出了每一步的相关系数（R）、相关系数的平方（R Square）、调整的相关系数的平方（Adjusted R Square）、估计值的标准误差（Std. Error of Estimate）。表下的脚注显示了每一步做预测的项目（包括自变量和常数项）。

➡️方差分析表

对每一步进行了方差分析，并列出了单独的方差分析表。

➡️系数分析表

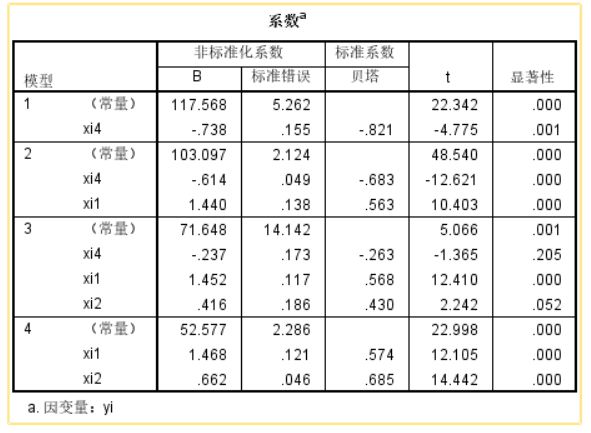
该表列出了每一步的各个自变量和常数项的非标准化系数（Unstandardized Coefficients）（包括变量X的待定系数（B）、常数项取值（B）及标准误差（Std. Error））、标准化系数（Standardized Coefficients）（Beta值）、t值、显著性水平（Sig.）。

➡️剔除变量表

本例中，用逐步回归法得到多元回归方程式为：
yi=52.577+1.468xi1+0.662xi2
模型的相关系数为0.989。

1.4 模型预测

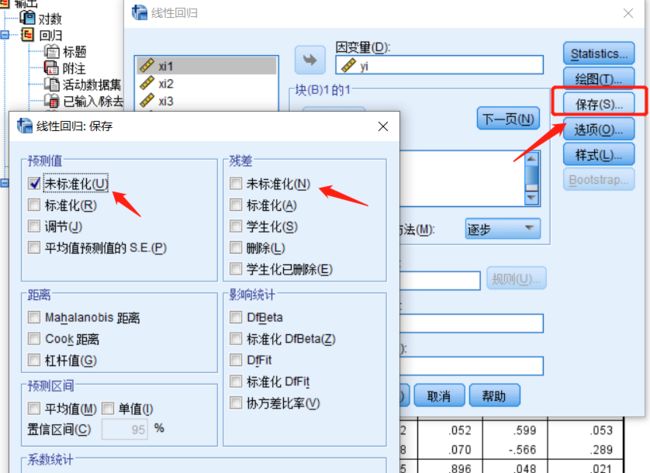
保存这一栏中选择预测值和残差后，在原始数据表中就会多出两列，一列是预测值，一列是残差。

二、聚类分析

在实际工作中，我们经常会遇到样品或指标的分类问题。根据事先是否已经建立类别，分类问题又可以分为判别分析和聚类分析。判别分析研究事先已经建立类别的情况，即将样品或指标按已知的类别进行归类；聚类分析则适用于事先没有分类的情况，即如何将样品或指标进行分类的问题。聚类分析包含的内容很广泛，可以有系统聚类法、k均值聚类法、动态聚类法、分裂法、最优分割法、模糊聚类法、图论聚类法、聚类预报等多种方法。主要介绍系统聚类法。

系统聚类法是聚类分析中应用最为广泛的一种方法，它的基本原理是，首先将一定数量的样品或指标各自看成一类，然后根据样品（或指标）的亲疏程度，将亲疏程度最高的两类进行合并。然后考虑合并后的类与其他类之间的亲疏程度，再进行合并。重复这一过程，直至将所有的样品（或指标）合并为一类。

2.1 提出问题

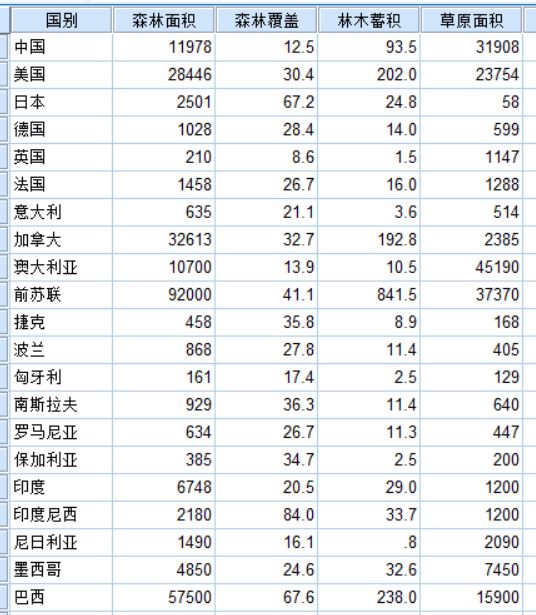
2.2 数据格式

2.3 SPSS操作

由于是对个案聚类，采用Q型聚类。在数据编辑器中打开文件“资源.sav”。在“分析”主菜单中用鼠标指向“分类”菜单项，然后在打开的子菜单中单击 “系统聚类”选项，打开“系统聚类分析”对话框，然后在“个案标注依据”输入框中输入变量名“国别”，在“变量”列表框中输入其他变量名，其他控件按默认设置。运行过程，生成如下各表：

➡️个案处理摘要
表中为有效个案、缺失个案和个案总数的个数和百分比。脚注显示聚类时采用的是距离度量方法，具体聚类方法为默认设置，即欧氏距离平方值和组间平均联结法

➡️凝聚计划(要看懂)

表中的各项意义如下：
（1）“阶段” 聚类步骤号。
（2）“组合聚类” 在某步中合并的个案。如第一步中第7个个案和第15个个案合并以后用第一项的个案号表示生成的新类。
（3）“系数” 距离或相似系数，由聚类分析的基本原理可知，个案之间亲密程度最高的，即距离最小或相似系数最接近于1或-1的最先合并。因此该列中的系数与第一列的聚类步骤相对应，系数值从小到大排列。
下面两段比较难理解，看不懂的话建议多看几遍：
（1）“首次出现聚类的阶段” 对应于各聚类步骤的参与合并的两项中，如果有一个是新生成的类（即由两个或两个以上个案合并成的类），则在对应列中显示出该新类在哪一步第1生成，如第4步中该栏第一列显示值为3，表示进行合并的2项中第1项是在第3步第1次生成的新类。从第3步可以看出，第4步的第1项是由第4个个案和第14个个案合并而成的新类。如果值为0，则表示对应项还是个案（不是新类）。
（2）“下一个阶段” 表示对应步骤生成的新类将在第几步与其他个案或新类合并。如第一行的值6表示第1步聚类生成的新类将在第6步与其他个案或新类合并。

➡️垂直冰柱图

表中第1列为聚类步骤号，第1行为个案及个案号。如果个案或（和）新类在第n步合并，则图中第n步以上合并项对应列之间的列中用“X”填充，没有空格。
现在参照聚结表从下往上解读该图。从聚结表中可以看出，聚类第1步为第7个个案和第15个个案合并，而冰柱图中对应于第20步，第7个个案与第15个个案对应的列之间在第20步以上用“X”填充。聚结表中第2步为第11个个案和第16个个案合并，而冰柱图中对应于第19步，第11个个案与第16个个案对应的列之间在第19步以上用“X”填充。如此继续下去，直至所有个案聚为一类。最后形成的图形中，由填充“X”构成的阴影条形就像屋檐下倒挂的冰凌一样，因此称为冰柱图。

在前面设置的基础上，在“系统聚类分析”对话框中单击“统计”按钮，打开“系统聚类分析：统计”对话框，然后在该对话框中选择两个复选框，选择“单个解”单选按钮，并在后面的输入框中输入数值“2”

运行过程，生成如下各表：

➡️近似值矩阵

表中为各个个案两两之间的欧氏距离平方值。

➡️聚类成员

该表为个案聚为两类时的个案归类表。表中分别给出了各个案所属的类别。由于前苏联与其他国家相比，在4项指标上比其他国家高出很多，因此被单独归为一类，而其他国家归为一类。

在前面设置的基础上，在“系统聚类分析”对话框中单击“图”按钮，打开“系统聚类分析：图”对话框，选择“谱系图、”复选框。在“系统聚类分析：方法”对话框中的“标准化”下拉式列表框中选择“Z得分”选项，然后单击“继续”按钮，回到“系统聚类分析”对话框中，单击“确定”按钮，运行过程，生成谱系图。

➡️谱系图

该图清晰地表示了聚类的全过程。它将实际的距离按比例调整到0～25的范围内，用逐级连线的方式连接性质相近的个案和新类，直至并为一类。在该图中上部的距离标尺上根据需要（粗分或细分）选定一个划分类的距离值，然后垂直标尺划线，该垂线将和水平连线相交。则相交的交点数即为分类的类别数，相交水平连线所对应的个案聚成一类。如果进行粗分，选择标尺值15，则所有个案分为两类，“前苏联”作为一类，其他国别作为一例。如果进行细分，选择标尺值4，则所有个案分为五类，“前苏联”作为一类，“巴西”作为一类，“中国”和“澳大利亚”作为一类，“匈牙利”、“尼日利亚”、“意大利”、“印度”、“英国”、“美国”、“加拿大”、“日本”和“印度尼西亚”作为一类，其他国别作为一类。当然，也可以选择中间值，将个案分为3类或4类。

三、判别分析

判别分析是利用原有的分类信息，得到体现这种分类的函数关系式（称之为判别函数，一般是与分类相关的若干个指标的线性关系式），然后利用该函数去判断未知样品属于哪一类。因此，这是一个学习和预测的过程。
常用的判别分析方法有距离判别法、费歇尔判别法和贝叶斯法等。根据处理变量的方式的不同，又可以分为典型法和逐步法。

3.1 提出问题

3.2 数据格式

3.3 SPSS操作

➡️分析个案处理摘要

表中列出了有效、排除以及总计的个案数和百分比。

➡️组统计

表中包括各个类别以及总和的未加权和加权的有效值。

➡️特征值

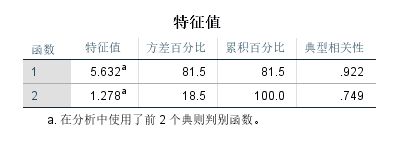
表中各项为前两个判别函数的特征值、方差百分比、累加百分比和典型相关性。最大特征值对应于组均值最大扩展方向上的特征值向量，第二大特征值对应于组均值次大扩展方向上的特征值向量，如此类推。特征值的平方根提供了对应特征值向量的长度信息，或该维的典则变量均值的宽度。对于本例，第一个典则变量解释了81.5%的总方差。

➡️威尔克Lambda

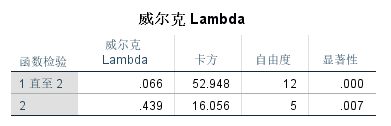
表中各项分别为威尔克Lambda、卡方、自由度和显著性。**当显著性概率小于0.05时，拒绝原假设，认为组间均值不相等。**表中第一行假设3个组中两个函数的均值相等，第二行则在剔除了第一个函数以后检验3个组中函数的均值相等。

➡️标准化典则判别函数系数

包括各独立变量对应的判别函数的标准化的系数值。根据该表可以得到判别函数：

ƒ1=0.142×食品＋0.545×衣着＋0.719×燃料＋0.709×住房＋0.063×生活＋0.208×文化
ƒ2=0.104×食品＋0.051×衣着＋0.482×燃料－0.037×住房－0.699×生活＋0.264×文化

注意，判别函数的个数为k-1或p中的小值，其中k为组数，p为变量个数。这里，由于组数为3，所以判别函数的个数为2，它比变量个数小。

➡️结构矩阵

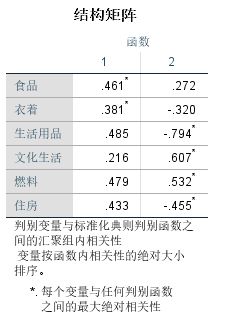
表内为判别变量与根据函数内相关系数绝对大小排序的标准化公共判别函数变量之间的合并组内相关系数。

➡️组质心处的函数

包括对应于前两个函数的各类别的函数值。
在前面设置的基础上，打开“判别分析：统计”对话框和“判别分析：分类”对话框，在其中选择所有的复选框，运行过程，生成如下各表：
➡️组统计

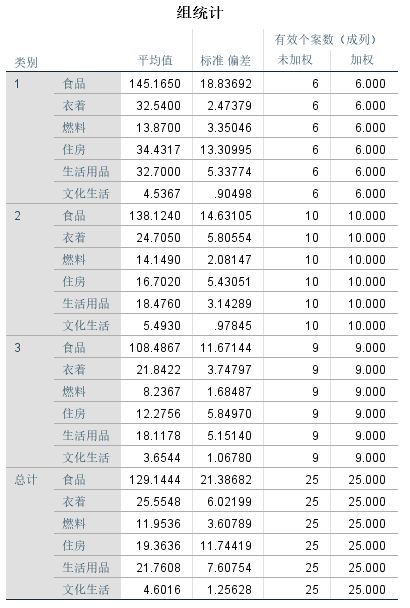
表中列出的是各个类别以及总和对应的各个变量的平均值、标准差、未加权和加权的有效个案数。

➡️组平均值的同等检验

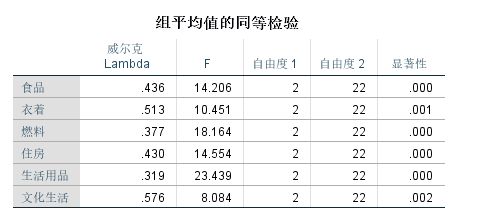
包括各变量对应的威尔克Lambda、F、自由度1、第二个自由度2和显著性。该检验的零假设是组均值是相等的，没有显著差异。由于该表中各变量对应的显著性概率均小于0.05，所以拒绝原假设，认为各变量的组均值存在显著差异。

➡️汇聚组内矩阵

表中为各变量两两之间的协方差和相关系数。

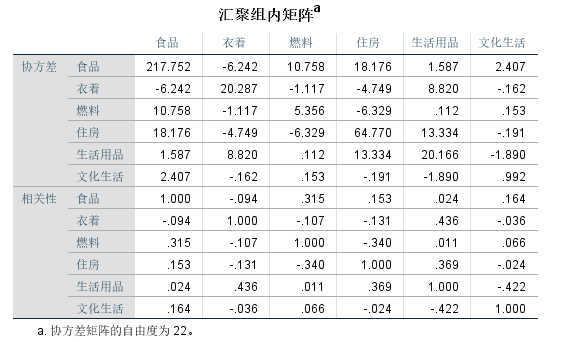
➡️协方差矩阵
包括各个类别和全部对应的各变量两两之间的协方差。

➡️对数决定因子
包括各类别和合并组内对应的秩和对数行列式。

➡️检验结果

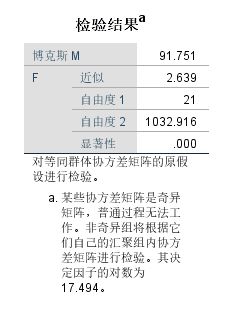
表中列出了博克斯值、近似F值、自由度1、自由度2和显著性。零假设为组的协方程矩阵相等。由于显著性概率小于0.05，所以拒绝原假设，认为协方差矩阵不相等，即差异显著。

➡️典则判别函数系数

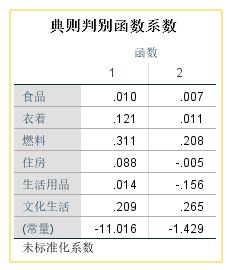
表中列出的是个变量及常数项对应的没有进行标准化的典型判别函数系数。利用该表，可以得到前两个判别函数的表达式：
ƒ1=0.010×食品+0.120×衣着+0.311×燃料+0.088×住房+0.014×生活+0.209×文化-11.016
ƒ2=0.007×食品+0.011×衣着+0.208×燃料-0.005×住房-0.156×生活+0.265×文化-1.429

➡️组的先验概率

包括各类别和全部对应的先验概率、未加权和加权的个案数。由于在“判别分析：分类”对话框中选择了“所有组同等”单选按纽，各类别的先验概率等于1除以类别数。本例中，类别数等于3，所以各类别的先验概率均等于1/3=0.333。

➡️分类函数系数

利用该表得到3个类别的分类判别函数为：

ƒ1=0.478×食品+1.625×衣着+2.492×燃料+0.581×住房+0.954×生活+5.224×文化-117.363
ƒ2=0.471×食品+1.378×衣着+2.233×燃料+0.351×住房+0.534×生活+5.357×文化-89.033
ƒ3=0.427×食品+0.964×衣着+0.832×燃料+0.0732×住房+4.179×生活+4.179×文化-53.373

将3个待判样本的变量数据代入3个函数中，每个样本对应得个函数的值进行比较，其中值最大的那个是第几个函数，则该样本判为第几类。计算后会发现北京、上海和广州3个城市对应的3个函数值都是第一个函数值最大，所以它们都划分为第1类。

四、主成分分析

4.1基本数学原理

因子分析的任务是构造一个因子模型，确定模型中的参数，然后根据分析结果进行因子解释；再对公共因子进行评估，并做进一步分析。
因子分析的一般模型为：

x1 = a11F1 + a12F2 + … + a1nFn + ε1
x2 = a21F1 + a22F2 + … + a2nFn + ε2
…
xm = am1F1 + am2F2 + … + amnFn + εm 式中x1, x2,…,xm为实测变量；aij（i=1,2,…,m；j=1,2,…,n）为因子荷载；Fi（i=1,2,…,m）为公共因子；εi（i=1,2,…,m）为特殊因子。

因子荷载aij是第i个变量在第j个主因子上的荷载，或者说，第i个变量和第j个主因子的相关系数。荷载越大，则说明第i个变量在第j个主因子的关系越密切；荷载较小，则说明第i个变量在第j个主因子的关系越疏远。因子荷载矩阵中各行数值的平方和，称为各变量对应的共同度。
公共因子是在各个变量中共同出现的因子，在高维空间中，它们是相互垂直的坐标轴。
特殊因子实际上是实测变量和估计值之间的残差值。如果特殊因子为零，则称为主成分分析。
为了使找到的主因子更易于解释，往往需要对因子荷载矩阵进行旋转，旋转的方法有很多，最常用的是最大方差旋转法（Varimax），进行旋转的目的是，就是要使因子荷载矩阵中因子荷载的平方值向0和1两个方向分化，使大的荷载更大，使小的荷载更小。
因子旋转过程中，如果因子对应轴相互正交，则称为正交旋转；否则称为斜交旋转。常用的方法有Promax法等。
将因子表示为变量的线性组合时，所得到的计算结果称为因子得分，它是对公共因子的估计值。利用它，可以做进一步的分析。

4.2 提出问题

4.3 数据格式

4.3 SPSS操作

在数据编辑器中打开数据集“污染.sav”，在“分析”主菜单中用鼠标指向“降维”选项，然后在打开的子菜单中单击“因子”选项，打开“因子分析”对话框，在该对话框中设置选项，进行因子分析，各选项的意义如下：
➡️"变量”列表框
用箭头按钮从左边列表框中移入想要分析的变量名。本例中的6个变量全部移入。
➡️“选择”输入框
在该输入框中输入变量名，对应变量用于限制对含有指定值的个案集合进行分析。单击“值”按钮，在打开的对话框中的“选择值”输入框中输入数值，确定选择该数值作为指定值。选好以后，单击“继续”按钮，回到“因子分析”对话框。
➡️“描述”按钮
单击该按钮，在打开的对话框中设置描述统计量。
（1）“统计”方框 设置统计量
“单变量描述”复选框 选择此项，计算并生成单变量描述统计量，包括每个变量有效测值的个数、均值和标准离差。
“初始解”复选框 选择此项，计算并生成初始解，包括变量的初始共同度、因子特征值、各特征值占特征值之和的百分比以及累计百分数。
（2）“相关性矩阵”方框 设置与相关矩阵有关的统计量
“系数”复选框 选择此项，生成相关系数。
“显著性水平”复选框 选择此项，生成相关矩阵中系数的单侧显著性水平。
“决定因子”复选框 选择此项，生成相关矩阵的行列式。
“KMO和巴特利特球形度检验”复选框 选择此项，进行KMO检验和Bartlett 球度检验。KMO可用做取样足够性的度量，用它可以检验变量的偏相关系数是否小，一般要求KMO值与1接近越好，当小到一定值时认为是不可接受的。Bartlett 球度检验可用于检验相关矩阵是否为一个单位矩阵，如果是单位矩阵，则认为模型是不合适的。
“逆”复选框 选择此项，生成相关矩阵的逆矩阵。
“再生”复选框 选择此项，生成再生相关矩阵，并给出相关矩阵与再生相关矩阵数据的差值。
“反映像”复选框 选择此项，生成反镜像相关矩阵。
➡️“提取”按钮
单击该按钮，在打开的对话框中进行提取因子的设置。
（1）“方法”下拉式列表框 提供因子提取的方法，共7种
“主成分”选项 用于组成实测变量的不相关线性集合，第一个因子具有最大方差，随后的因子依次代表逐渐减少的方差，并且彼此无关。主成分法用于获得初始因子解，在相关矩阵为奇异时可用。
“未加权最小平方”选项 该方法使实测相关系数和再生相关系数的差值的平方和最小。
“广义最小平方”选项 与上面的方法近似，但相关系数用它们的逆进行加权，具有较高惟一的变量被赋予较小的权重。
“最大似然估计”选项 如果样本来自多变量正态总体，该方法给出相关矩阵中系数的参数估计，相关系数用逆值进行加权，并且采用了迭代的方法。
“主轴因式分解” 选项 该法将来自初始相关矩阵的多个相关系数平方放在对角线上，作为公共因子的初始估计。这些因子荷载用于估计新的公共因子，并代替旧的公共因子。该方法同样使用迭代法。
“Alpha因式分解”选项 α因子提取法。该法将分析的变量当作来自潜在变量全域的一个样本，使因子的α可靠性最大化。
“镜像因式分解”选项 变量的公共部分称为偏镜像，定义为现存变量的线性回归。
（2）“分析”方框 设置分析内容
“相关性矩阵”单选按钮 为默认选项。选择此项，计算相关矩阵。
“协方差矩阵”单选按钮 选择此项，计算协方差矩阵。
（3）“输出”方框 设置显示内容
“未旋转因子解”复选框 为默认选项。选择此项，显示没有旋转因子的因子荷载矩阵、公共因子和特征值。
“碎石图”复选框 选择此项，显示碎石图。该图是与每个因子相关的方差的图形。
（4）“提取”方框 设置有关因子提取的原则和规模
“基于特征值”单选按钮 为默认选项。选择此项，在后面的输入框中输入数值，确定提取特征大于该数值的因子。该数值的缺失值为1。
“因子的固定数目”单选按钮 选择此项，在后面的输入框中输入数值，确定提取因子的数目。
（5）“最大收敛迭代次数”输入框 在输入框中输入最大迭代次数。默认值为25。
➡️“旋转”按钮
单击该按钮，在打开的对话框中进行有关矩阵旋转的设置。
（1）“方法”方框 设置进行旋转的方法
“无”单选按钮 为默认选项。选择此项，不进行旋转。
“最大方差法”单选按钮 该法使在每个因子上具有较高荷载的变量个数最小化。它简化因子的解释，用于正交旋转。
“直接斜交法”单选按钮 该法用于非正交旋转。当δ等于0（为默认值）时，解的倾斜最大。当δ的负性越强，因子的倾斜越小。输入小于或等于0.8的数值可以覆盖δ的默认值。
“四次幂极大法”单选按钮 使解释每个变量的因子个数最小化。该法使实测变量的解释简化。
“等量最大法”单选按钮 该法是最大方差法的组合，有较大荷载作用于因子上的变量数和用于解释变量的因子数最小化。
**“最优斜交法”单选按钮 倾斜旋转，它允许因子相关，计算时比直接斜交法法快，因此用于大的数据集合。**在下面大“Kappa”输入框中输入一个数，用于控制该法的计算，默认值为4。
（2）“输出”方框 设置显示项
“旋转后的解”复选框 该控件在选择上面五种旋转方法之一时可用。对于正交矩阵，显示旋转模式矩阵和因子转换矩阵；对于倾斜矩阵，显示模式矩阵、结构和因子相关矩阵。
“载荷图”复选框 选择此项，显示前3个因子的3维因子荷载兔；对于两因子的求解，输出二维图。
“最大收敛迭代次数”输入框 在输入框中输入最大迭代次数。默认值为25。
➡️“得分”按钮
单击该按钮，在打开的对话框中进行有关因子得分的设置。
（1）“保存为变量”复选框 选择此项，将得分因子保存为新变量
（2）“方法”方框 设置计算因子得分的方法
“回归”单选按钮 为默认选项。选择此项，用回归的方法计算因子得分。
“巴特利特”单选按钮 选择此项，用Bartlett法计算因子得分，用该法计算时，均值为0，变量范围内惟一因子的平方和最小化。
“安德森—鲁宾”单选按钮 选择此项，用Anderson—Robin 法计算因子得分，该法是Bartlett法的修改，能保证估计因子的正交性，因子得分均值为0，标准差为1，且不相关。
（3）“显示因子得分系数矩阵”复选框 选择此项，显示因子得分系数矩阵。
➡️“选项” 按钮
单击该按钮，在打开的对话框中设置缺失值的处理方式和系数显示格式
（1）“缺失值”方框 设置缺失值的处理方式
“成列排除个案”单选按钮 为默认选项。选择此项，剔除所有含有缺失值的个案数据。
“成对排除个案”单选按钮 选择此项，剔除当前正在分析的成对变量中含有缺失值的个案数据
“替换为平均值”单选按钮 选择此项，用均值代替缺失值。
（2）“系数显示格式”方框 设置系数的显示格式。
“按大小排序”复选框 选择此项，根据大小排序。
“排除小系数”复选框 选择此项，在后面的输入框中输入一个正数，确定系数的绝对值不得大于该数值。

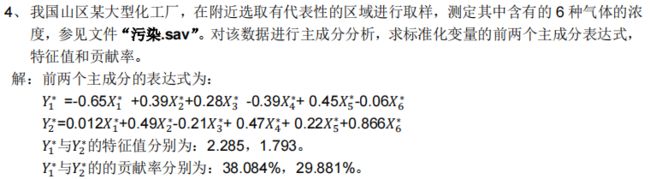
4.4 例题SPSS操作

对于本例，在打开的“因子分析”对话框中，单击“提取”按钮，在打开的对话框中，选择“分析”方框中“相关性矩阵”单选按钮，选择“提取”方框中“基于特征值”单选按钮，在后面的输入框中输入数值0.6。运行过程，得到如下各表：

➡️公因子方差

该表给出了各变量对应的初始共同度和提取因子以后的再生共同度。表的注脚显示采用主成分分析法提取因子。

➡️总方差解释表该表各列的意义如下：

（3）成分
（4）初始特征值
①总计 特征值。特征值的大小反映公因子的方差贡献。
②方差百分比 特征值占方差的百分数。
③累积% 特征值占方差百分数的累计值。
（3）“提取载荷平方和” 该栏为根据特征值大于0.6的原则提取的4个因子的特征值、占方差的百分数及其累计值。这4个因子所解释的方差占整个方差的95.517% ，能比较好地反应所有信息。
注：如果选择的是“分析”方框中“协方差矩阵”单选按钮，则该栏为根据特征值大于平均特征值的0.6倍的原则提取因子。而且总方差解释表中“初始栏”为针对原始数据计算的结果；“提取栏”为将原始数据按比例缩放后计算的结果。

➡️因子荷载矩阵

表中各列为对应于各变量的4个主因子的荷载值。由该表可得到提取4个主因子时的因子模型：

氯=-0.975F1+0.01631F2-0.0464F3-0.00224F4 
硫化氢=0.592F1+0.654F2-0.120F3-0.402F4
SO2=0.424F1	-0.287F2+0.848F3+0.104 F4
碳4=-0.584F1+0.631F2+0.199F3+0.385F4 
环氧=0.674F1+0.299F2-0.280F3+0.598F4
环己=-0.092F1+0.891F2+0.315F3-0.144F4

将各因子表达为变量的表达式，则得到因子得分函数，如下所示：

F1=-0.975氯 +0.592硫化氢+0.424 SO2 -0.584碳4+ 0.674环氧-0.092环己
F2=0.01631氯+0.654 硫化氢-0.287 SO2+ 0.631碳4+ 0.299环氧+0.891环己
F3=-0.046氯-0.120硫化氢+0.848 SO2+0.199碳4-0.280环氧+0.315环己
F4=-0.00224氯-0.402硫化氢+0.104 SO2+ 0.385碳4+ 0.598环氧-0.144环己

值得注意的是：

最终得出的主成分线性表达式需要用因子得分函数/sqrt(特征值)
例如：Y1 = -0.975/sqrt(2.285)+ 0.592/sqrt(2.285)+…

五、非参数检验

非参数方法可以广泛应用于社会科学、行为科学、生物科学和数理科学等研究领域。与参数方法相比，它具有分布自由，可用于按数值意义讲并不严格但有一定等级顺序的资料的分析以及计算简单三大优点。
将鼠标指向“分析”主菜单中的“非参数检验”选项，再点击“就对话框”选项，打开子菜单。单击子菜单中的选项，将进行不同的检验。子菜单中的选项有：
1.卡方检验。
2.二项检验。
3.游程检验
4.单样本 K-S检验
5.2个独立样本的检验
6.K个独立样本的检验
7.2个相关样本的检验
8.K个相关样本的检验
下面分别介绍应用于其中四种不同情况的非参数检验方法。

5.1 两个独立样本的非参数检验

两个独立样本的非参数检验包括 Mann-Whitney U检验、Kolmogorov-Smirnov双样本检验、 Wald-Wolfowitz游程检验和Moses极端反应检验等方法。

①对话框介绍
在“非参数检验”子菜单中单击“2个独立样本”选项，打开“双独立样本检验”对话框。对话框中各选项的意义如下。

➡️ “检验变量列表”列表框 在该列表框中输入变量名，对应变量的数据作为检验对象。
➡️ “分组变量”输入框 在该输入框中输入变量名，则对应的变量作为分组变量，该变量名后面添加小括号，小括号内有两个问号，用“定义组”按钮做进一步设置。
➡️ “定义组”按钮 单击该按钮，打开“双独立样本：定义组”对话框。在对话框中的“组1”输入框和“组2”输入框内分别输入数值（这两个数值分别代表分组变量的不同取值），将根据输入的值在原数据中选取分组数据。
➡️ “检验类型”方框 在该方框内进行选择，确定用什么方法进行检验。

• “曼-惠特尼”检验
• “柯尔莫戈洛夫-斯米诺夫”检验
• “莫斯极端反应”检验
• “瓦尔德-沃尔福威茨游程”检验

➡️ “选项”按钮 单击该按钮，打开“双独立样本检验：选项”对话框。该对话框设置统计量的描述和缺失值的处理。
“统计”方框 该方框内的选项设置统计量描述选项。
“描述”复选框 选择此项，计算并显示数据个数、均值、标准离差、最小值和最大值等统计量。
“四分位数”复选框 选择此项，计算并显示四分位数
“缺失值”方框 该方框中内的选项用来设置缺失值的处理方式。
“按检验排除个案”单选按钮 为默认选项。选择此项，剔除进行检验的数据中存在缺失值的个案。
“成列排除个案”单选按钮 选择此项，剔除所有含有缺失值的个案。

②“曼-惠特尼”检验

基本数学原理：该检验可用来检验两个独立样本是否取自同一个总体，它是最强的非参数检验之一，用该方法进行检验时，先将两个样本放在一起，并对所有的个案按升序排列，计算样本二的每个观测值大于样本一的每个观测值的次数，分别用U1和U2表示。若U1和U2比较接近，则说明两个样本来自相同分布的总体。若U1和U2差异较大，则说明两个样本来自不同的总体。

5.1.1提出问题

K-S检验补充：
“柯尔莫戈洛夫-斯米诺夫”检验
基本数学原理 ：该检验可用来检验两个独立样本是否取自同一个总体，进行检验时，对每个观察样本做累加频数分布，并对分布采用相同的间隔，对于每个间隔，将两个阶梯函数相减，并着重分析观测值的差值中间的最大者。
对于单尾检验，令D = max [ Fn1(x) - Fn2(x) ]
对于双尾检验，令D = max | Fn1(x) - Fn2(x) |
式中，Fn1(x)和Fn2(x)分别为两个样本的观测累加阶梯函数，如果D较小，则可以认为两个样本取自同一个总体；如果D较大，大到一定程度，则可以认为两个样本不是取自同一个总体的。

5.1.2 数据格式

5.1.3 SPSS操作

SPSS实现：在“双独立样本检验”对话框中输入变量以后，在“检验类型”方框中选择“柯尔莫戈洛夫-斯米诺夫”复选框，并做其他设置，运行过程，将采用“柯尔莫戈洛夫-斯米诺夫”双样本数据的检验。


表中，显著性概率（Asymp.Sig.）小于5%，因此，否定原假设，即认为两个年级的学生先学的材料时犯错误的次数是不同的。

5.2 多个独立样本的非参数检验

多个独立样本的非参数检验方法有3种：Kruskal-Wallis H法、中位数法和Jonckheere-Terpstr法。
①对话框介绍
在“非参数检验”子菜单中单击“K个独立样本”选项，打开“针对多个独立样本的检验”对话框。该对话框中各选项的意义如下。
➡️“检验变量列表”列表框 用右箭头按钮从源变量名列表框中输变量名到该列表框中，对应变量的数据将作为检验对象。
➡️“分组变量”输入框 在该输入框中输入变量名，对应变量用做分组变量，用“组定义”按钮定义取值范围。
➡️“组定义”按钮 单击该按钮，打开“多个独立样本：定义范围”对话框。在该对话框中的“最小值”输入框和“最大值”输入框中分别输入数值，作为取值范围的下限和上限。
➡️“检验类型”方框 在该方框中选择一种检验方法。有克鲁斯卡尔-沃利斯H法、中位数法和约克海尔-塔帕斯特拉法3种。
➡️“选项”按钮 这个按钮的用法参见前面相关内容。
②克鲁斯卡尔-沃利斯H检验
基本数学原理：该检验用来检验K个独立样本是否来自不同总体，若这K个样本服从相同分布，则在样本容量不太小的情况下，下面的统计量H服从自由度K-1的χ2分布 LaTex公式教程
$$H=12/(N(N+1))\sum R_j^2/n_j-3（N+1）（j从1到k求和）$$
式中，k为样本数，nj为第j个样本中的个案数，N为所有样本的个案数之和， Rj 为第j个样本（列）中的秩和。

该法是Mann-Whitney U检验的推广，它不要求数据服从正态分布，因而在一定情况下可以代替F检验。

5.2.1 提出问题

5.2.2 数据格式

5.2.3 SPSS操作

数据编辑器中打开该数据文件，打开“针对多个独立样本的检验”对话框，在“检验变量列表”列表框中输入变量名“个性评分”，在“分组变量”输入框中输入变量名“教师”，单击“组定义”按钮，打开“多个独立样本的检验：组定义”对话框，在“最小值”输入框和“最大值”输入框中分别输入数值“1”和“3”，单击“继续”按钮，回到“多个独立样本的检验”对话框，单击“确定”按钮，生成以下各表。

表中由于显著性概率小于5%，因此否定原假设，即认为这3种教育工作者的权威主义是有差异的。

5.3 两个相关样本的非参数检验

两个相关样本的非参数检验包括Wilcoxon符号秩检验、符号检验和McNemar检验。
①对话框介绍
在“非参数检验”子菜单中单击“2个相关样本”，打开“双关联样本检验”对话框。对话框中各选项的意义如下：
➡️“检验对”列表框 选定配对变量以后用右箭头按钮输入到该列表框中，作为待检验的对象。
➡️“检验类型”方框 在该方框中进行选择，确定用什么方法进行检验。可供选择的方法有“威尔科克森”符号秩检验、“麦克尼马尔”检验和“边际齐性”检验。
➡️“选项”按钮 单击该按钮，打开相应的对话框，可参照前面的内容进行设置。
②“威尔科克森”符号秩检验
基本数学原理：该检验不仅考虑了配对内差异的方向，还考虑到配对数据的相对大小，因此它比后面将要讲到的符号检验要强。
应用“威尔科克森”符号秩检验法进行检验时，首先将所有配对数据的评分差按绝对值大小评秩，然后对每一个秩附加不同的符号，用正号表示来自正的评分差的秩，用负号表示来自负的评分差的秩。如果两个相关样本等价（没有差别），则将对应于正号的秩和对应于符号的秩分别求和以后，两个和值大致相等。如果两个和值相差很大，则两个样本差异较大。

SPSS实现：在数据编辑器中输入数据以后，打开“双关联样本检验”对话框，输入变量对以后，在“检验类型”方框内选择“威尔科克森”复选框，将对数据进行“威尔科克森”符号秩检验。

5.3.1 提出问题

5.3.2 数据格式

5.3.3 SPSS操作

5.3.3.1 符号检验

在数据编辑器中打开该数据文件，然后打开“双关联样本检验”对话框，进行设置后，单击“确定”按钮，生成以下各表。


H0 : 两种饲料喂养的猪体重增量没有差异。从符号检验成果表得到显著性概率（Sig.）为0.021 ，小于 5%，因此拒绝原假设，两种饲料喂养的猪，体重增量有差异。

5.3.3.2 Wilcoxon 符号秩检验

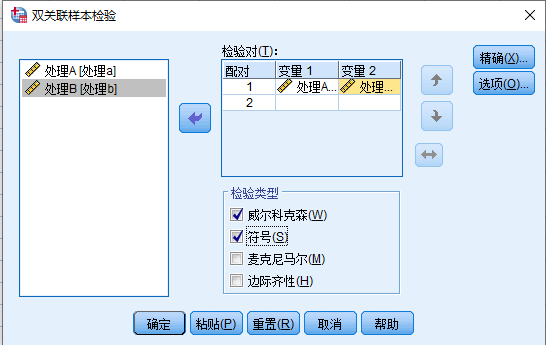
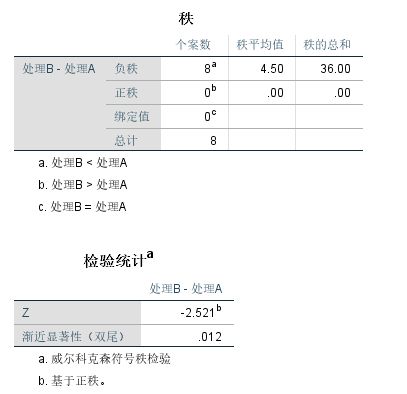
H0 : 两种方法对于小麦的收成没有差异。从 Wilcoxon 符号秩检验成果表中得到显著性概率（Sig.）为 0.012，小于 5%，因此拒绝原假设，即认为以上两种处理方法是有差异的，将导致不同的小麦产量。

5.4、多个相关样本的非参数检验

多个相关样本的非参数检验方法包括Friedman检验、Kendall协和系数检验和Cochran’s Q 检验。
①对话框介绍
在“非参数检验”子菜单中单击“K个相关样本”选项，打开“针对多个相关性样本的检验”对话框。在对话框中，在“检验变量”列表框中输入多个变量名，对应变量数据作为检验对象。在“检验类型”方框中进行选择，确定进行检验的方法。可供选择的有“傅莱得曼”检验、“肯德尔W”检验和“柯克兰Q”检验3种方法。
②傅莱得曼检验
基本数学原理：该法检验k个相关样本是否来自同一总体，进行检验时，首先建立一个N行k列的双向表，当下面的统计量近似服从自由度为 k-1的χ2分布时，认为秩和无显著性差异，这k个相关样本来自同一总体，否则否定零假设。
$${\chi }_2=12/（N_k（k+1））\sum R_j^2-3N（k+1）（j从1到k求和）$$
式中， N为行数，k为列数，Rj为第j列的秩和。

SPSS实现：在数据编辑器中输入数据以后，打开“针对多个相关性样本的检验”对话框，在“检验变量”列表框中输入变量以后，在“检验类型”方框输入“傅莱得曼”复选框，单击“确定”按钮，将对样本数据进行“傅莱得曼”检验。

5.4.1 提出问题

5.4.2 数据格式

5.4.3 SPSS操作

在数据编辑器中打开该数据文件，打开“针对多个相关性样本的检验”对话框，进行设置后，单击“确定”按钮，生成秩表和“傅莱得曼”检验统计表。表中，显著性概率小于5%，因此，否定前面的假设，即认为不同的强化方式对老鼠的学习情况有显著影响。

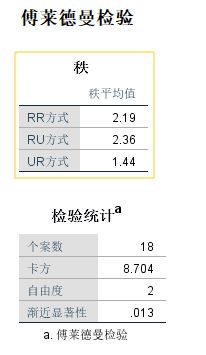
H0 : 不同的强化方式对老鼠的学习情况没有显著影响。从 Friedman 检验成果表中得到显著性概率（Sig.）为 0.013 ，小于 5%，因此拒绝原假设，即认为以上三种方式是有差异的

---