HBU-NNDL 作业11：优化算法比较

 

目录

 1. 编程实现图6-1，并观察特征

 2. 观察梯度方向

 3. 编写代码实现算法，并可视化轨迹

4. 分析上图，说明原理

        1、为什么SGD会走“之字形”？其它算法为什么会比较平滑？

        2、Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

        3、仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

        4、四种方法分别用了多长时间？是否符合预期？

        5、调整学习率、动量等超参数，轨迹有哪些变化？

5. 总结SGD、Momentum、AdaGrad、Adam的优缺点

6. Adam这么好，SGD是不是就用不到了？

7. 增加RMSprop、Nesterov算法。

8. 基于MNIST数据集的更新方法的比较

总结

---

 

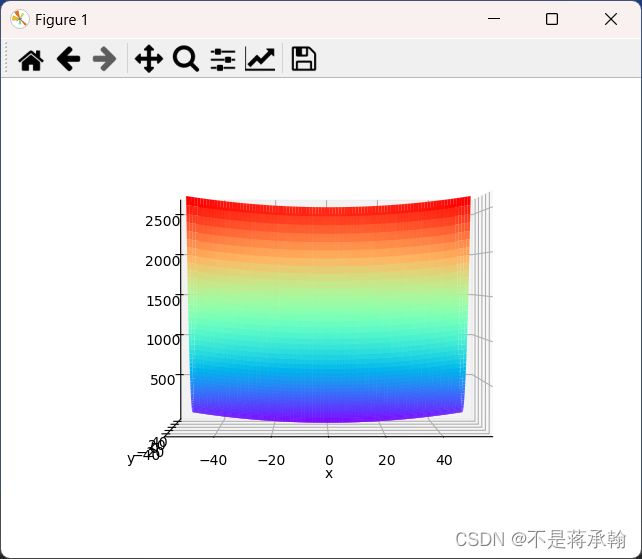
 1. 编程实现图6-1，并观察特征

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def func(x, y):
    return x * x / 20 + y * y


def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数

    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)

    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')

    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()


paint_loss_func()

 

 这个函数最底下是一条弧线，所以有全局最小值。

 

 2. 观察梯度方向

         由于函数底部的那条弧线弧度很小，所以梯度下降方向基本是沿着y轴方向，x轴方向只占很小一部分，很多地方都梯度也没有指向（0，0）处。

 3. 编写代码实现算法，并可视化轨迹

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


class Momentum:
    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]


class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]


class AdaGrad:
    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:
    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)


def f(x, y):
    return x ** 2 / 20.0 + y ** 2


def df(x, y):
    return x / 10.0, 2.0 * y


init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
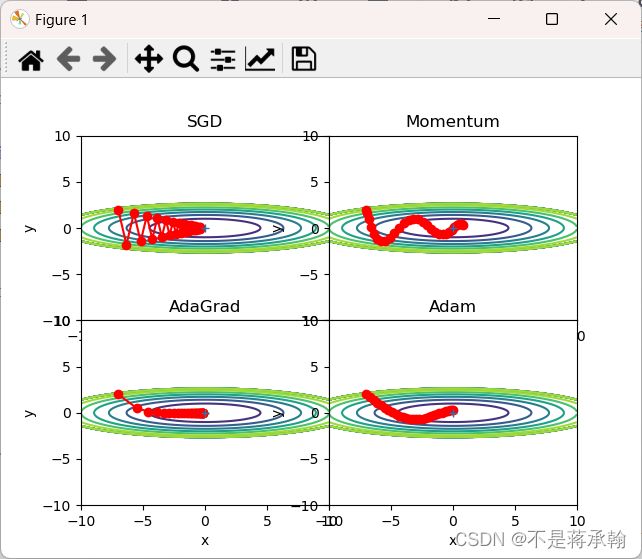
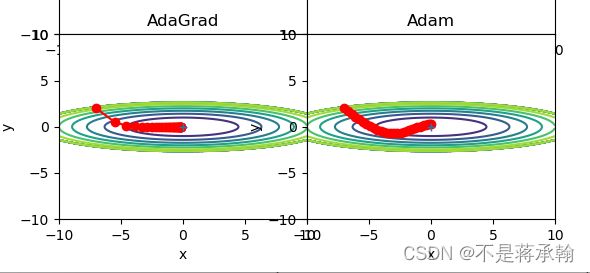
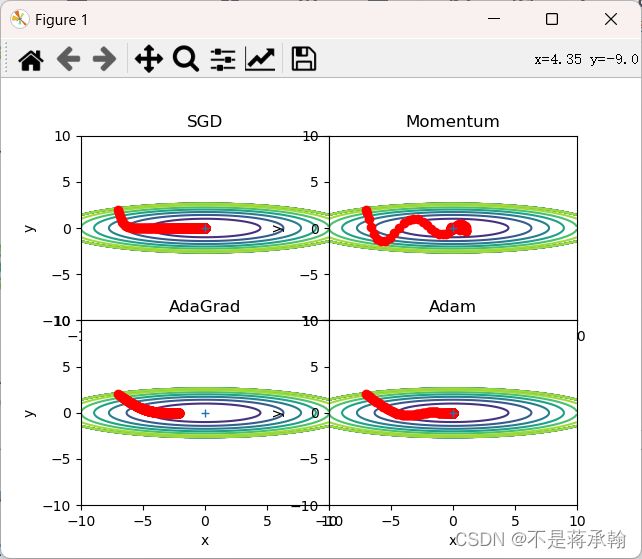
plt.show()

 

         根据使用的方法不同，参数更新的路径也不同。只看这个图的话，AdaGrad似乎是最好的，不过也要注意，结果会根据要解决的问题而变。并且，很显然，超参数（学习率等）的设定值不同，结果也会发生变化。

         那么用哪种方法好呢？非常遗憾，（目前）并不存在能在所有问题中都表现良好的方法。这4种方法各有各的特点，都有各自擅长解决的问题和不擅长解决的问题。 很多研究中至今仍在使用SGD。Momentum和AdaGrad也是值得一试的方法。最近，很多研究人员和技术人员都喜欢用Adam。

4. 分析上图，说明原理

        1、为什么SGD会走“之字形”？其它算法为什么会比较平滑？

        SGD呈“之”字形移动。这是一个相当低效的路径。也就是说， SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索 的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的SGD更聪 明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。

        2、Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

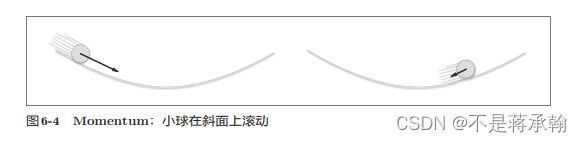
Momentum是“动量”的意思，和物理有关。用数学式表示Momentum方 法，如下所示。

        和前面的SGD一样，W表示要更新的权重参数， 表示损失函数关 于W的梯度，η表示学习率。这里新出现了一个变量v，对应物理上的速度。 式（6.3）表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增 加这一物理法则。如图6-4所示，Momentum方法给人的感觉就像是小球在 地面上滚动。 

 

 

        上图中，更新路径就像小球在碗中滚动一样。和SGD相比，我们发现 “之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱“之”字形的变动程度。

---

        AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习 （AdaGrad的Ada来自英文单词Adaptive，即“适当的”的意思）。下面，让我们用数学式表示AdaGrad的更新方法。

和前面的SGD一样，W表示要更新的权重参数， 表示损失函数关于W的梯度，η表示学习率。这里新出现了变量h，如式(6.5)所示，它保存了以前的所有梯度值的平方和。 然后，在更新参数时，通过乘以 ，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。 

 

由上图的结果可知，函数的取值高效地向着最小值移动。由于y轴方 向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按 比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之” 字形的变动程度有所衰减。

        3、仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

从轨迹来看，好像是这样，主要有以下两点原因：

1、Adam可能不收敛

         AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这会使得学习率不断递减，最终收敛到0，模型也得以收敛。

        但Adam则不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

2、Adam可能错过全局最优解

深度神经网络往往包含大量的参数，在这样一个维度极高的空间内，非凸的目标函数往往起起伏伏，拥有无数个高地和洼地。有的是高峰，通过引入动量可能很容易越过；但有些是高原，可能探索很多次都出不来，于是停止了训练。

        4、四种方法分别用了多长时间？是否符合预期？

从上往下依次是SGD，Momentum，AdaGrad，Adam的运行时间

可以看出，Adam因其算法复杂度而运行时间最长，其他三种算法时间差不多。

        5、调整学习率、动量等超参数，轨迹有哪些变化？

lr=0.01时：

 lr太小，30次根本不够搜索的，改为1000次

 这次Momentum找到了最小点，Adam马上找到，而其他两种算法还差得多

lr=0.1，搜索1000次

 

只有AdaGrad没有找到最小点 

 lr=1，搜索1000次

lr=100，搜索100次 

 

 可以发现，SGD和Momentum很容易错过全局最小值，Adam需要较长的时间和较多的搜索次数来找到全局最小值，AdaGrad效果最好。

5. 总结SGD、Momentum、AdaGrad、Adam的优缺点

SGD：

选择合适的learning rate比较困难 - 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征，有时我们可能想更新快一些对于不经常出现的特征，对于常出现的特征更新慢一些，这时候SGD就不太能满足要求了。

SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点

Momentum：

• 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的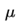能够进行很好的加速 

• 下降中后期时，在局部最小值来回震荡的时候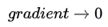，， 使得更新幅度增大，跳出陷阱 

• 在梯度改变方向的时候，能够减少更新 总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛

Adagrad ：

• 前期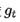较小的时候， regularizer较大，能够放大梯度 

• 后期较大的时候，regularizer较小，能够约束梯度 

• 适合处理稀疏梯度 

由公式可以看出，仍依赖于人工设置一个全局学习率 

设置过大的话，会使regularizer过于敏感，对梯度的调节太大 

中后期，分母上梯度平方的累加将会越来越大，使，使得训练提前结束 

Adam：

• 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点 

• 对内存需求较小 

• 为不同的参数计算不同的自适应学习率 

• 也适用于大多非凸优化 - 适用于大数据集和高维空间 

6. Adam这么好，SGD是不是就用不到了？

参考：Adam那么棒，为什么还对SGD念念不忘 (2)—— Adam的两宗罪_gukedream的博客-CSDN博客

先来看SGD。SGD没有动量的概念，也就是说：

代入

计算当前时刻的下降梯度：

可以看到下降梯度就是最简单的

 
SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。

SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这两类算法会使得学习率不断递减，最终收敛到0，模型也得以收敛。

但AdaDelta和Adam则不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得  可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

Adam很可能错过全局最优解

深度神经网络往往包含大量的参数，在这样一个维度极高的空间内，非凸的目标函数往往起起伏伏，拥有无数个高地和洼地。有的是高峰，通过引入动量可能很容易越过；但有些是高原，可能探索很多次都出不来，于是停止了训练。

近期Arxiv上的两篇文章谈到这个问题。

第一篇就是前文提到的吐槽Adam最狠的 The Marginal Value of Adaptive Gradient Methods in Machine Learning 。文中说到，同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

另外一篇是 Improving Generalization Performance by Switching from Adam to SGD，进行了实验验证。他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

于是他们提出了一个用来改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错。

所以，谈到现在，到底Adam好还是SGD好？这可能是很难一句话说清楚的事情。去看学术会议中的各种paper，用SGD的很多，Adam的也不少，还有很多偏爱AdaGrad或者AdaDelta。可能研究员把每个算法都试了一遍，哪个出来的效果好就用哪个了。

而从这几篇怒怼Adam的paper来看，多数都构造了一些比较极端的例子来演示了Adam失效的可能性。这些例子一般过于极端，实际情况中可能未必会这样，但这提醒了我们，理解数据对于设计算法的必要性。优化算法的演变历史，都是基于对数据的某种假设而进行的优化，那么某种算法是否有效，就要看你的数据是否符合该算法的胃口了。

另一方面，Adam之流虽然说已经简化了调参，但是并没有一劳永逸地解决问题，默认参数虽然好，但也不是放之四海而皆准。因此，在充分理解数据的基础上，依然需要根据数据特性、算法特性进行充分的调参实验，找到自己炼丹的最优解。而这个时候，不论是Adam，还是SGD，于你都不重要了。

7. 增加RMSprop、Nesterov算法。

optimizers['RMSprop']=RMSprop(lr=0.2)
optimizers['Nesterov']=Nesterov(lr=0.1)

对比Momentum与Nesterov

两个算法都是动量优化法，Nesterov项是momentum的改进，在梯度更新时做一个校正，让之前的动量直接影响当前的动量，避免前进太快，同时提高灵敏度。

对比AdaGrad与RMSprop

两个都是自适应学习率优化法，RMSprop解决了对历史梯度一直累加而导致学习率一直下降的问题，适合处理非平稳目标，对于RNN效果很好，但RMSprop依然依赖于手动选择全局学习率。

8. 基于MNIST数据集的更新方法的比较

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

从结果中可知，与SGD相比，其他3种方法学习得更快，而且速度基本相同，仔细看的话，AdaGrad的学习进行得稍微快一点。这个实验需要注意的地方是，实验结果会随学习率等超参数、神经网络的结构（几层深等）的不同而发生变化。不过，一般而言，与SGD相比，其他3种方法可 以学习得更快，有时最终的识别精度也更高。

总结

        因为这部分内容在鱼书中是在RNN之前，所以在学RNN之前就读过了，就对参数更新优化算法有了一定了解，再加上上学期学的最优化方法，这次上课的内容对我来说就不是很难。