用python动手学统计学_3-4用python模拟抽样
用python模拟抽样
基于阿里云天池
3-4-1环境准备
#用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
#用于绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
#设置浮点数打印精度
%precision 3
#在jupyter notebook里显示图形
%matplotlib inline
3-4-2抽样过程
样本就是随机变量,它的取值会随机变化。
3-4-3在只有5条鱼的湖中抽样
使用numpy中的数组准备鱼的体长数据
fish_5 = np.array([2,3,4,5,6])
fish_5
# array([2, 3, 4, 5, 6])
np.random.choice
使用np.random.choice函数从5条鱼中随机抽取一部分,size=1表示将样本容设定为1,replace =False表示函数不重复选取相同的值
随机选取1条鱼
np.random.choice(fish_5,size = 1,replace= False)
# array([4])
随机选取3条鱼
np.random.choice(fish_5,size = 3,replace= False)
# array([6, 3, 2])
每次的结果都不想同,得到的是随机样本
随机种子
设置随机种子,每次执行的多得到的样本相同
np.random.seed(1)
np.random.choice(fish_5,size = 3,replace= False)
# array([4, 3, 6])
计算所得样本的平均值,即样本均值
np.random.seed(1)
sp.mean(np.random.choice(fish_5,size = 3,replace= False)
# array([4, 3, 6])
)
#4.333333333333333
3-4-4随机数
随机得到的数字叫做随机数。有些领域将其看作随机变量。模拟抽样也是一种生成随机数的过程。
3-4-5放回抽样、不放回抽样
把抽出的样本放回总体再重新抽样叫做放回抽样。抽出的样本不放回总体的抽样叫做不放回抽样。
指定参数replace = False的抽样就是不放回抽样。
3-4-6从鱼较多的湖中抽样
读入数据化为列联表
读入数据
fish_10000 = pd.read_csv(
"tongji_data/3-4-1-fish_length_100000.csv")["length"]
fish_10000.head()
# 0 5.297442
# 1 3.505566
# 2 3.572546
# 3 3.135979
# 4 4.689275
# Name: length, dtype: float64
计算个数
len(fish_10000)
# 100000
抽取十条鱼,使用np.random.choice()
sampling_result = np.random.choice(
fish_10000,size = 10,replace = False)
sampling_result
# array([4.091, 5.465, 3.426, 4.287, 4.244, 4.282, 4.29 , 5.087, 2.769,
# 5.296])
最后计算样本均值
sp.mean(sampling_result)
#4.3235970793805025
3-4-7总体分布
均值,即总体分布
sp.mean(fish_10000)
# 4.000000000000001
总体的标准差
sp.std(fish_10000,ddof=0)
# 0.8
求方差
sp.var(fish_10000,ddof=0)
# 0.64
绘制总体的直方图
sns.distplot(fish_10000,kde=False,color='black')
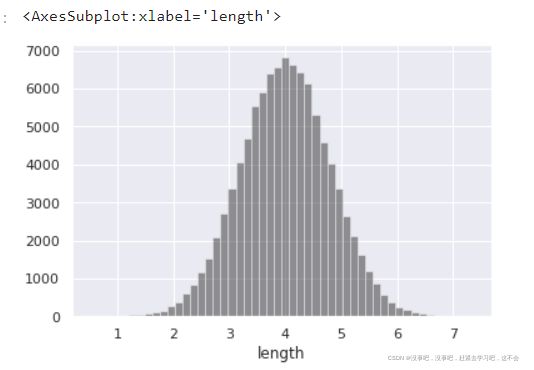
均值为4、方差0.64
方差的公式:1-7上以0.1为公差的等差数列
3-4-8对比总体分布和正态分布的概率密度函数
准备1-7上以0.1为公差的等差数列
x = np.arange(start = 1,stop =7.1,step = 0.1)
x
# array([1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1, 2.2,
# 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2, 3.3, 3.4, 3.5,
# 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8,
# 4.9, 5. , 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1,
# 6.2, 6.3, 6.4, 6.5, 6.6, 6.7, 6.8, 6.9, 7. ])
使用函数stats.norm.pdf计算概率密度。参数loc为均值,scale为标准差。
stats.norm.pdf(x = x,loc = 4,scale = 0.8)
# array([4.407e-04, 6.988e-04, 1.091e-03, 1.676e-03, 2.536e-03, 3.778e-03,
# 5.540e-03, 7.998e-03, 1.137e-02, 1.591e-02, 2.191e-02, 2.971e-02,
# 3.967e-02, 5.215e-02, 6.749e-02, 8.598e-02, 1.078e-01, 1.332e-01,
# 1.619e-01, 1.938e-01, 2.283e-01, 2.648e-01, 3.025e-01, 3.401e-01,
# 3.764e-01, 4.102e-01, 4.401e-01, 4.648e-01, 4.833e-01, 4.948e-01,
# 4.987e-01, 4.948e-01, 4.833e-01, 4.648e-01, 4.401e-01, 4.102e-01,
# 3.764e-01, 3.401e-01, 3.025e-01, 2.648e-01, 2.283e-01, 1.938e-01,
# 1.619e-01, 1.332e-01, 1.078e-01, 8.598e-02, 6.749e-02, 5.215e-02,
# 3.967e-02, 2.971e-02, 2.191e-02, 1.591e-02, 1.137e-02, 7.998e-03,
# 5.540e-03, 3.778e-03, 2.536e-03, 1.676e-03, 1.091e-03, 6.988e-04,
# 4.407e-04])
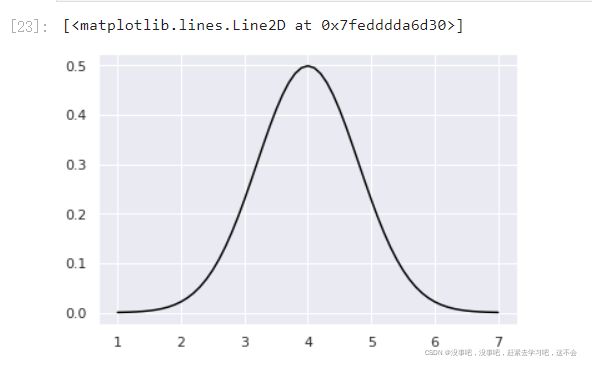
绘制概率密度函数
plt.plot(x,
stats.norm.pdf(x = x,loc = 4,scale = 0.8),
color = 'black')
是以均值为轴左右对称的平滑的概率分布
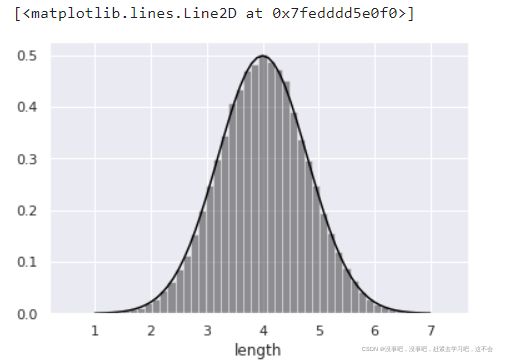
最后,把正态分布的概率密度图形和总体的直方图叠放
norm_hist = True,可以得到总面积为1的直方图
sns.distplot(fish_10000,kde=False,
norm_hist = True,color='black')
plt.plot(x,
stats.norm.pdf(x = x,loc = 4,scale = 0.8),
color = 'black')
3-4-9抽样过程的抽象描述
使用函数stats.norm.rvs函数。参数loc为均值,scale为标准差,size为样本容量。
sampling_norm = stats.norm.rvs(
loc = 4,scale = 0.8,size = 10)
sampling_norm
# array([4.037, 3.498, 4.322, 5.295, 5.499, 2.905, 4.437, 4.665, 3.786,
# 4.569])
样本均差
sp.mean(sampling_norm)
# 4.3014016645
3-4-10有限总体校正
1.严格来说正态分布的概率密度的图形和直方图不是完全等价。
假设总体分布为正态分布,这句话的含义是,假设总体为无限总体,组数有无穷多个,组的大小,组的大小也分得无穷习,则它的直方图和直方图不是完全等价的。
2.stats.norm.rvs函数生成随机数的过程却是从无限总体中进行抽样。要想基于有限总体,就需要进行有限总体校正。当总体容量远大于样本容量时,无需进行校正。
3-4-11假设总体服从正态分布是否恰当
严格来说,总体分布不是正态分布,但实践假设多会假设总体服从正态分布。
正态分布可以取负数。事实上,即使假定体长服从正态分布,它取负数的概率也小到可以忽略不计,因而可以大胆采用正态分布。
参考资料
[日] 马场真哉 著, 吴昊天 译. 用Python动手学统计学[M]. 1. 人民邮电出版社, 2021-06-01.
菜鸟网站python3