脑皮质算法（3）-- 新皮层的位置:利用皮层网格细胞的感觉运动物体识别理论

Locations in the Neocortex: A Theory of Sensorimotor Object Recognition Using Cortical Grid Cells

摘要

新大脑皮层能够预测运动的感觉结果，但对其神经机制知之甚少。在内嗅皮层中，网格细胞代表了动物在环境中的位置，这个位置通过运动和路径整合而更新。在这篇论文中，我们提出感觉新皮层使用网格细胞样神经元来表示传感器在物体上的位置，从而整合运动。我们描述了一个双层神经网络模型，该模型使用皮质网格细胞和路径集成来通过运动鲁棒地学习和识别物体，并预测运动后的感官刺激。由若干网格单元格组成的单元格层表示特定对象在参考框架中的位置。另一层负责处理感官输入的细胞将这个位置输入作为上下文，并利用它在物体的参考框架中对感官输入进行编码。感官输入使网络调用先前学习过的与输入一致的位置，而运动输入使网络更新这些位置。仿真结果表明，该模型可以学习数百个对象，即使仅靠对象特征不足以消歧。我们讨论了模型与皮层回路的关系，并认为第4层和第6层之间的互反连接符合模型的要求。我们提出皮质柱的超颗粒层采用网格细胞样机制来表示通过移动更新的对象特定位置。

关键词： 新皮层，感觉运动学习，网格细胞，物体识别，分级时间记忆

简介

我们的大脑通过处理我们的感官输入和动作来了解外部世界。当我们触摸一个物体、观察一个视觉场景或探索一个环境时，大脑会接收到一系列的感觉和动作，即感觉运动序列。

传统上被认为是感觉区域的皮层区域是将运动流整合到它们的处理过程中的。在视觉中，我们感知到的是一个稳定的世界图像，通常忽略了我们的眼睛每秒进行多个眼跳运动的事实。当眼睛移动时，视觉皮层中许多代表特定刺激的神经元会在刺激到达细胞的感受野之前预测到刺激(Duhamel et al.， 1992)。在听觉方面，听觉皮层的反应会被运动信号预测性地抑制(Schneider和Mooney, 2018)。在躯体感觉中，当我们的手指在熟悉的物体上移动时，我们很快就会注意到差异，这表明我们对特定的物体做出了特定的触觉预测。

预测感觉运动加工也发生在海马的形成中。网格细胞(Hafting et al.， 2005)和位置细胞(O 'Keefe and Dostrovsky, 1971)代表动物的位置，它们结合了感官地标和自我运动线索来更新它们的活动(Campbell et al.， 2018)。当动物到达一个先前存在的物体丢失的地方时，另一组神经元会选择性地变得活跃(Tsao等人，2013年)，这表明该系统具有预测性。

因此，大脑中似乎在认知中扮演不同角色的不同区域显示出两种常见计算的特征:对感觉运动序列的信息整合，以及对运动后的感觉刺激的预测。目前还不清楚神经元网络如何从一系列感觉和动作中提取可重复使用的信息，以及如何利用这些信息预测后续序列的感觉结果。简单的记忆感觉运动序列会导致过多的学习需求，因为对于每一个被感知的物体都有许多可能的感觉运动序列。

我们实验室最近的工作(Hawkins et al.， 2017)提出，新皮层通过将感觉运动序列转换为以物体为中心位置的感觉特征序列来处理感觉运动序列。然后，新大脑皮层学习并识别物体作为物体参考框架中位置的感官特征集，它通过参考这些学习到的物体模型来预测感官输入。这种方法将运动整合到物体识别中，并形成物体的表征，在新的运动序列中进行归纳。然而，在那篇论文中，我们没有讨论计算这种位置信号的神经机制。

本文通过展示新皮层如何表示和计算以物体为中心的位置，扩展了我们之前的工作。利用这种方法，我们提出了一种神经网络模型，通过处理动作序列来学习和识别目标。我们将传感器定义为皮肤或视网膜的一小块，为大脑皮层的一个特定的小块提供输入，这个小块大脑皮层可以被认为是一个皮层柱(Mountcastle, 1997)。从海马体如何预测环境中的感觉刺激中获得灵感，该模型使用网格细胞模拟表示传感器相对于物体的位置，并将该位置与感觉输入联系起来。然后，它可以通过使用运动信号来预测感官输入，计算传感器的下一个位置，然后回忆与该位置相关的感官特征。我们提出，处理来自一个小的感觉补丁的输入的新皮层的每个补丁，包含了使用感觉和运动学习和识别物体所需的所有电路。信息也在斑块之间水平交换，因此识别并不总是需要移动(Hawkins et al.， 2017)，然而，本文关注的是发生在每个单独的皮层斑块内的计算。

在熟练运动行为的背景下，感觉运动整合和学习内部模型有着丰富的历史(Wolpert和Ghahramani, 2000;Wolpert et al.， 2011)。这些课程主要集中在学习运动动力学和运动控制，如到达和抓取任务。本文主要研究一个互补问题，即在感觉和运动的基础上整合信息来学习和表征外部对象。

在本文的其余部分，我们首先回顾了内嗅皮层网格细胞的基本性质。然后我们提出，新皮层使用网格细胞的类似物来模拟物体，就像海马组织使用网格细胞来模拟环境一样。基于Hawkins等人(2017)提出的理论框架，我们提出每个新皮层柱都包含该模型的一个变体。基于皮层解剖，我们提出第6层的细胞使用网格细胞一样的机制来表示物体特定的位置，通过移动更新。我们建议第4层使用来自第6层的输入来预测感官输入。

网格单元格如何表示位置和移动

我们首先回顾了内嗅皮层中的网格细胞如何表示空间和位置。尽管网格单元功能的许多细节仍然未知，但对于一些原则已经形成了普遍共识。在这里，我们关注两个对我们的模型非常关键的属性:位置编码和路径集成。

单个网格单元在环境中的多个位置变得活跃，通常在类似网格的重复三角形网格中(图1A)。这些三角形的边长称为网格单元格的刻度。网格单元模块是一组网格单元，它们以相同的尺度和方向激活，但发射位置不同，因此一个或多个网格单元将在任何位置激活(图1B)。如果您根据模块中的相对发射位置对网格单元进行排序，它们将形成菱形瓷砖。当动物移动时，活动的“碰撞”会穿过这个菱形(图1B、C)。细胞在该同形中的二维位置称为细胞的空间相位，模块的种群活动可以近似地用活动凸点的空间相位来描述。单个模块中的活动提供了动物的位置信息，但这些信息是模糊的;环境中的许多位置可以导致相同的活动。

为了形成一个独特的表示，需要多个网格单元模块具有不同的尺度或方向(图1C,D)。为了便于说明，假设我们有10个网格单元模块，每个模块可以通过一个活动凸起编码25个可能的位置。这10个凸起表示动物的当前位置。请注意，如果动物在一个方向连续移动，单个模块的活动将由于平铺而重复，但由于模块之间的规模和方向的差异，10个模块的集成活动不太可能重复。这种编码所形成的表征能力是很大的。在我们的例子中，可以表示的唯一位置的数量是2510≈1014。Fiete等人(2008)和Sreenivasan和Fiete(2011)对网格代码的容量和噪声鲁棒性进行了综述。

当动物移动时，模块中的活动网格细胞会发生变化，以反映动物的更新位置。即使动物处于黑暗中，这种变化也会发生(Hafting et al.， 2005)，这告诉我们网格细胞是根据动物运动的信息更新的。这个过程被称为“路径整合”，它具有一个理想的特性，即无论运动路径如何，当动物返回到相同的物理位置时，相同的网格细胞将被激活(图2A)。路径整合是不精确的，因此在学习过的环境中，感官地标被用来“锚定”网格细胞，防止路径整合错误的积累(McNaughton等人，2006;Ocko等人，2018)。

最后一个重要的属性是位置表示对于每个环境都是唯一的。如果，在第一次进入一个新环境时，每个网格单元模块激活一个随机碰撞来表示当前位置，那么随着动物在环境中移动，所有模块之间的表示很可能是唯一的。因此，初始随机起点隐式地为每个环境定义了唯一的位置空间，包括尚未显式访问的位置。由于每个模块独立集成运动信息，路径集成属性自动适用于每个新环境。因此，路径集成可以为每个模块学习一次，然后在所有环境中重用。每个新环境的位置空间将是可能的单元活动的整个空间的一个很小的子集(在我们上面的示例中，整个空间包含2510个点)，因此表示环境的容量是相当大的。当重新进入之前学习过的环境时，感官线索和网格细胞之间的联系被用来“重新锚定”或重新激活之前的位置空间(Barry et al.， 2007)。

综上所述，一组网格单元格模块可以明确地表示环境中的位置。这些位置可以通过移动进行路径集成，环境地标可以用来纠正路径集成错误。通过在模块中选择随机起点，可以为每个环境定义惟一的位置空间。所有可能的细胞激活空间随着模块的数量呈指数增长，因此表示位置和环境的容量很大。

模型

我们认为网格细胞在整个新皮层中都存在。我们提出，皮质网格细胞不是代表动物在环境中的位置，而是代表感觉斑块的位置，例如，在一个物体的参考框架中，指尖(图2B)。与传统的网格细胞类似，皮质网格细胞在每个物体周围定义了一个独特的位置空间。当传感器移动时，代表每个感知补丁位置的网格细胞群将通过独特的位置空间进行路径集成。因此，物体上特征的相对位置可以作为消除歧义和识别物体的有力线索。

我们的网络模型通过感觉运动序列整合信息，将独特的位置空间与物体联系起来，然后识别这些位置空间。为了概述这一机制，让我们首先考虑一个问题:老鼠是如何识别熟悉的环境的?它必须使用它的感官输入，但单一的感官观察可能不足以唯一地识别环境。因此，老鼠需要移动并进行多次观察。

为了结合来自多个感官观察的信息，大鼠可以利用每次观察来回忆与该特征相关的所有位置集合。当它移动时，它可以执行路径集成来更新每个可能的位置。随后的感官观察将用于缩小位置集，并最终消除位置的歧义。在较高的水平上，这种通用策略是机器人领域的一组定位算法的基础，包括蒙特卡洛/粒子滤波定位、多假设卡尔曼滤波和马尔可夫定位(Thrun等人，2005年)。

我们的模型使用这种策略来识别带有移动传感器的物体。该模型使用每个感知特征来回忆它之前感知到的位置，同时激活这些之前学习到的位置表示。当传感器移动时，移动信号导致网络更新每个位置，从而对这组位置执行路径集成。这个更新的位置预测了一组可能的特征，而感官输入被用来确认这些预测的子集。随着每一次后续的感觉，网络将缩小这个位置列表，直到它唯一地识别出一个特定物体上的特定位置，这个位置与感觉和运动的顺序一致。

当位置已知时，每个网格单元格模块将有单个活动凸点(当在图1B中排序的菱形中查看时)。在我们的模型中，当网络接收到的信息不足以消除位置的歧义时，每个网格单元模块通过激活多个凸起来捕获这种歧义，每个凸起对应与目前输入序列匹配的可能位置。我们将这组同时活动的表示称为位置的联合。在运动过程中，网络会移动这些凸起的组合，就像它会单独移动每个凸起一样。当网络接收到更多的输入时，与输入不一致的活动位置将会被剔除，并集将会缩小，直到每个模块出现一个碰撞。

已知感官特征会触发与熟悉环境相关的网格细胞活动(Barry et al.， 2007)，但大脑学习这些关联的机制尚不清楚。我们的模型通过简单地学习当前活动网格细胞和当前感知特征之间的关联来学习对象。随后，感知到这个特征，网络就会调用这个位置，当路径集成调用这个位置时，网络就会预测这个特征。

这种定位算法假设动物在其所处环境的参照系中始终知道自己的运动方向。确定这个方向需要动物首先进行航向检索，这个计算在某种程度上独立于大脑中的定位(Julian et al.， 2018b)。我们的模型不包括标题检索的模拟。该模型假设它接收到的运动向量是在对象的参考系中。在讨论中，我们简要描述了如何扩展该模型来执行标题检索的模拟，从而构建对象的方向不变模型。

模型描述

我们的双层模型由两组神经元和四组主要连接组成(图3)。在“映射到生物学”一节的后面，我们提出了哪些皮层群体实现了这个电路。对于传感器的每一次运动，网络都要经历一系列的阶段，处理电机输入和感官输入。每个阶段对应于使用来自图3中编号箭头之一的连接。我们在图4中展示了一个经过这些阶段三次的网络示例。

在阶段1中，电机输入先于感官输入，由定位层处理，定位层由网格单元模块组成。如果这一层有一个活动位置表示，它使用电机输入来移动每个模块的活动，计算传感器的新位置。

在第二阶段，这种更新的网格细胞活动传播到感觉层，并在该层引起一系列预测。

在第三阶段，感觉层接收实际的感觉输入。预测与感官输入相结合。新的活动是高度稀疏代码的联合。每个稀疏代码表示在特定位置的单个感官特征，与目前的输入一致。

在第四阶段，感觉层活动传播到位置层。每个模块根据感官表征激活网格细胞的联合。位置层将包含稀疏位置表示的联合，这些表示与目前的输入一致。

第四阶段之后，下一个运动动作开始，循环重复。接下来的几节将详细描述网络结构和这四个阶段中的每个阶段，以及学习过程。

网络结构

我们通过一组离散的时间步来计算网络活动。每一个时间步骤t都由上面列出的四个阶段组成。这里，我们先描述神经元模型和网络结构，然后详细描述各个阶段。

我们通过一组离散的时间步来计算网络活动。每一个时间步骤t都由上面列出的四个阶段组成。在每个时间点上，神经元不是活跃的就是不活跃的。在感觉层，每个神经元的输出是其两个输入的函数;没有额外的内部状态。在定位层中，神经元被排列成网格单元模块，当传感器移动时，活动的凸起在每个模块中移动，为每个神经元分配一个标量激活。这种激活状态是神经元内部的;当神经元的激活状态超过一个阈值时，它就是活跃的。这里，我们先描述神经元模型和网络结构，然后详细描述各个阶段。
网络中的每个神经元都有多个独立的树突段。在每个时间点上，一个树突片段要么是活跃的，要么是不活跃的，这影响着神经元是否变得活跃。每个节段都有一组突触，当它接收到足够数量的这些突触的输入时，节段就会变得活跃。$D_{c,d}^{loc}$和$D_{c,d}^{in}$分别表示位置层和感觉层细胞c上树突d的突触。突触权值要么为0，要么为1。学习后每个树突上的突触数量通常很少，因此这些向量高度稀疏。具有独立树突段的神经元模型与Poirazi-Mel神经元的结构(Poirazi and Mel, 2001)和锥体神经元中活性树突的现有实验文献密切相关(Antic et al.， 2010;Major et al.， 2013)。多个树突片段使每个神经元能够稳健地识别独立的稀疏模式，从而与多个位置或感官环境相关联。尽管单个神经元的活动可能是模糊的，但我们已经在Ahmad and Hawkins(2016)和Hawkins and Ahmad(2016)中表明，此类神经元网络的活动可以表示稀疏分布代码，这些代码在特定环境中高度独特。此外，有了足够多的单元格，稀疏表示使这样的网络能够表示模式的联合(Ahmad和Hawkins, 2016)，错误匹配错误的概率很低(在一定限度内)。

感官和位置层

这里展示的网络是Hawkins等人(2017)工作的延伸，感觉层在结构上与该论文中的感觉输入层相同。在那篇论文中，该层被组织成一组小柱(Buxhoeveden, 2002)，这样，在一个小柱内的所有细胞都有相同的前馈感受野，但彼此抑制。感觉层神经元的树突节段具有调节作用。活性段本身并不能使细胞变得活跃。当具有活性树突节段的细胞识别前馈输入时，该细胞将抑制小柱内没有活性节段的其他细胞(见下面的阶段3)。小列$i$的活动单元格用二进制数组$A_t^{in,i}$表示。层活动$A_t^{in}$由所有小列活动$A_t^{in,i}$的连接组成。

定位层结构为一组网格细胞模块，每个模块包含相同数量的神经元。模块i在t时刻的活动神经元用二进制数组 $A_t^{loc,i}$ 表示，层活动 $A_t^{loc}$ 由所有模块活动 $A_t^{loc,i}$ 拼接而成。这一层神经元的树突段具有驱动作用;如果细胞的任何一个树突片段变得活跃，细胞就会变得活跃。在推断过程中，位置层中的活动在响应移动时更新一次，然后在响应感官派生输入时再次更新。我们用向量$A_{t,move}^{loc}$ 和 $A_{t,sense}^{loc}$ 表示这两种激活状态。

定位层投射到感觉层的树突片段(图3，连接2)。因此，$D_{c,d}^{in}$是一个与$A_t^{loc}$长度相同的向量，其中1表示连接到定位层中的一个单元格。感觉层投射到位置层的树突片段(图3，连接4)。因此，$D_{c,d}^{loc}$是一个长度与$A_t^{in}$相同的向量，其中1表示连接到感觉层中的一个细胞。这些载体通常非常稀疏，因为它们在学习过程中连接到稀疏活动的细胞(参见下面的学习部分)。

在每个时间步中，接受足够输入的树突段变得活跃。二元向量${\pi }_t^{in}$和${\pi }_t^{loc}$表示每层中包含至少一个活性树突段的细胞。这表示每个细胞是否能从另一层的活动中预测出来。取${\theta }^{in}$和${\theta }^{loc}$为树状阈值，

阶段1:使用移动来更新位置层

定位层由一组独立的网格单元模块组成，每个模块都有自己的尺度和方向。我们遵循其他网格单元模型和分析的符号和假设(Sreenivasan和Fiete, 2011;Ocko等人，2018)。在模块中，活动的单元格总是位于模块贴图中某个位置(或阶段)中心的单元格活动高斯碰撞的一部分(图1B)。我们设模块i的凸相位为${\phi }_t^i$。模块内的每个细胞以一个相为中心，其在t时刻的活度与其与${\phi }_t^i$的接近程度成正比。网络通过更新每个模块的${\phi }_t^i$来响应移动命令。

移动将移动每个模块的凹凸根据模块的规模和方向。与每个模块相关联的二维变换矩阵$M_i$表示模块如何将传感器的运动向量转换为凹凸的运动向量。表示模i的尺度为$s_i$，方位为${\theta }_i$，则变换矩阵为:

这个操作将运动矢量转换成60◦基础，安排每个网格细胞的发射场成一个三角形而不是正方形晶格。它还缩放和旋转移动矢量，以设置网格的缩放和方向。

每个模块接收到相同的2D运动矢量$d_t$，它按如下方式移动它的凹凸:

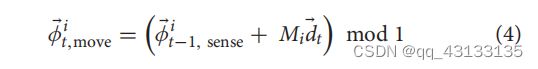
模运算将每个活动的凹凸限制在2D范围[0,1)×[0,1)内有一个相位。例如，在网格单元格模块的排序视图中(图1B)，相位[0.1,0.1]对应左下角，而[0.9,0.9]对应右上角。细胞活动的碰撞以这一阶段为中心，我们将碰撞建模为具有高斯形状，以定性地匹配观察到的网格细胞响应的发射场的形状(Monaco和Abbott, 2011)。

除了这些特性外，我们的模型还要求网格单元模块能够同时集成多个凸起。每个模块通过激活多个凸起表示不确定性，每个可能的位置对应一个凸起。我们称之为位置的联合。我们将模块的凸起集指定为8it。对于每个运动，我们将Eq.(4)应用到8it中的每个阶段，如下所示:

位置层中的每个模块不是显式地模拟单个单元动态，而是简单地维护活动碰撞阶段列表，并根据Eq.(5)更新每个阶段。然后，通过阈值模块中每个单元的内部标量激活状态，位置层输出二进制向量 $A_{t,move}^{loc}$ (见“模型细节”部分)。在讨论中，我们回顾了单个网格单元动力学模型，并讨论了它们与联合的兼容性。

阶段2：使用更新的位置来形成感官预测

在第二阶段，我们计算哪些感官特征是由位置层预测的。在我们的网络中，这些预测用${\pi }_t^{in}$表示，${\pi }_t^{in}$是感觉层细胞远端树突段的活性。我们用上面的式(1)从 $A_{t,move}^{loc}$计算${\pi }_t^{in}$。

在当前任何可能的位置遇到的每一个感官特征都将被预测。注意，因为 $A_{t,move}^{loc}$是所有网格单元格模块的连接，所以预测是基于高度特定的位置代码。

${\pi }_t^{in}$对感觉层的活动有调节作用，如第3阶段所述。

第三阶段:计算感觉层的活动

在第三阶段，感知层利用感知特征来确认正确的预测，并忽略不正确的预测。当任何预测都不正确时，它会激活该特征的所有可能的位置特征表示。这个阶段负责激活和缩小工会。

在Hawkins等人(2017)的研究中，感觉层与感觉输入层相同。在这一层，所有的细胞在一个小柱共享相同的前馈感受野。每一个感官特征都由一个小列的稀疏子集表示，用$W_t^{in}$表示。当一个细胞被预测时，它就准备好变得活跃，如果它接收到感官输入，它就会迅速激活和抑制小列中的其他细胞。

通过考虑$W_t^{in}$和考虑哪些细胞被定位层预测，即哪些细胞有活跃的树突段，来选择感觉层内的活性细胞。如果预测了一个单元格，并且它位于$W_t^{in}$中的一个迷你列中，那么它将变为活动的。如果$W_t^{in}$中的一个小列没有预测细胞，那么这个小列中的每个细胞都将被激活。这个激活逻辑可以表示为:

如果位置层已经唯一地识别了当前位置，那么在$W_t^{in}$的每个小列中都恰好有一个活动单元在当前位置编码这个感觉特征。如果位置层包含多个位置的联合，则感觉层将在多个位置的联合上表示该特征。注意，位置层可能预测$W_t^{in}$中没有表示的特征。这些小列在这一步之后将不包含任何活动(图4,Sensation 2)，可能的对象集因此被缩小了。

阶段4：基于感官提示更新定位层

在第4阶段，感觉层的活动回忆位置层的位置。$A_t^{in}$用于计算${\pi }_t^{loc}$[公式(2)]，它驱动位置层的活动。每个模块中的活动碰撞阶段列表被由感官输入驱动的一组新的碰撞所取代。对于定位层中具有相应活动树突段的每个细胞，模块激活以该细胞为中心的凸起，如下所示:

这组新的凸起通常与前一组非常相似，如图4、《Sensation 3》。注意，此步骤仅发生在推断期间。在学习过程中，位置层不响应感官输入而更新;我们简单地分配${\varphi }_{t,sense}^{loc,i}={\varphi }_{t,move}^{loc,i}$。

位置层$A_{t,sense}^{loc}$中的活动单元由${\varphi }_{t,sense}^{loc}$计算(参见“模型详细信息”部分)。请注意，由于从位置层到感觉层的连接不能驱动活动，网络中的递归是最小的(见“模型细节”部分)。

学习

在我们的模型中，学习过程包括将位置与感官特征联系起来，反之亦然。这些关联是在远端树突节段上学习的，如Eq.(8)和Eq.(9)所示。该模型中的学习总是由两层中形成互反连接的活性细胞组成。在新对象的训练开始时，位置层中的每个模块在随机阶段激活一个碰撞。这将实例化特定于该对象的随机位置空间。在接下来的训练中，我们提供一系列的运动和感觉输入，像以前一样计算${\varphi }_{t,move}^{loc}$，随着每个动作移动每个模块的碰撞。

每个感官输入都由一组小列$W_{t，sense}^{in}$表示。按照上面的式(6)，如果对象的这一部分还没有被学习到，在感觉层中就不会有预测，这些小列中的每个细胞都将变得活跃。在这种情况下，每个活动迷你列中的一个随机单元格被选择作为学习单元格，也就是说，在这个位置上表示这个感觉输入。如果对象的这一部分已经被学习，在感觉层就会有预测。在这种情况下，与现有活动段相对应的细胞被选中进行学习。$A_{t,learn}^{in}$表示当前时间步长的这些学习单元格。

在$A_{t,sense}^{loc}$和$A_{t,learn}^{in}$中，每个活跃的细胞都选择一个树突片段$d^{\prime }$，并在这一段和其他层的每个活性细胞之间形成如下连接:

这里，我们将“|”指定为位或，这意味着当这些新连接形成时，树突段上现有的连接不受影响。

仿真结果

我们运行了模拟来测试我们的模型学习物体结构的能力，并从运动序列中准确预测感官特征。我们的模型与特定的特征提取技术无关，因此我们专注于测试特征提取后发生的神经计算集。这些实验测试了这套神经计算，并不打算成为物体识别的通用基准。我们的目标是了解模型是否可以在感觉运动序列上积累信息，并了解模型何时达到断点。

在仿真中，模型的输入由感官特征和运动序列组成。该模型的任务是从单一的感觉运动序列中学习一个对象，然后从不同的感觉运动序列中识别该对象。在图5中，我们展示了测试对象和输入序列的插图。每个物体由10个点组成，从4乘4的网格中随机选择。我们在每个点放置一个特征，从固定的特征池中随机选择每个特征并进行替换。特征是跨对象共享的，一个给定的特征可以出现在同一对象的多个点上。
>

对于每个模拟，我们通过访问每个对象上的每个点一次来训练网络。对于每个点，我们将活动存储在单独的分类器中的位置层中。然后，我们通过随机遍历每个对象点来测试每个对象上的网络。重要的是，网络为每一个特征之间的随机转换接收一个电机输入，使它能够随着时间正确地积累信息。当传感器遍历对象时，我们测试位置表示是否与对象上该点的分类器存储表示完全匹配。如果它与这种表示相匹配并且这种表示对这个对象是唯一的，我们就认为这个对象是可识别的。如果在经过物体四次后，网络始终没有收敛到一个单一的位置表示，或者收敛到一个错误的位置，我们认为这是识别失败。(在这些实验中，模型总是要么收敛到单一位置，要么根本不收敛。)网络有可能收敛于正确的位置表示，即使该位置对对象来说不是唯一的，例如，如果模块的数量不足以创建唯一的代码。在后面的章节中，我们将特别说明这种情况发生的时间。

我们设置感觉层有150个小柱，每个小柱有16个细胞。每个感官特征激活一个预先确定的、随机选择的10个小列集合，其中包含时间步t的$W_{t,sense}^{in}$。我们改变每个模块的单元数和定位层中的模块数。对于这些模拟，我们改变了模块的方向，但没有改变尺度。方向沿可能的方向的60◦范围均匀间隔。每个模块使用相同的比例，这个比例被固定为对象最大宽度的一半。我们将树突阈值${\theta }^{loc}$和${\theta }^{in}$分别设为8和$[n\ast 0.8e]$，其中n为定位层中的模块数，$[]$为天花板算子(向上舍入，ceiling操作)。

细胞活动收敛到唯一的位置表示

我们首先演示了一个典型的识别任务中的细胞活动，并展示了它如何随着网络学习更多的对象而变化。在图6中，当网络感知到不同的对象时，我们显示了位置层中几个模块的实际网格单元活动。该网络首先在50个对象上进行训练，每个对象从40个特征池中提取10个特征。活动随着每个新感觉的变化而变化，首先通过基于运动的路径集成转移，然后将活动缩小到只与新感觉特征一致的位置。该网络可以接受不同数量的感觉，以缩小到单一的位置表示。一旦网络缩小，单个模块中的活动可能是模糊的，但跨所有模块的活动单元集(仅显示10个模块中的3个)惟一地编码了对象和位置。

识别过程总是遵循这个模板。最初的感觉输入通常会引起密集的激活，假设感觉特征不是单一位置所独有的。随着随后的动作和感觉，这种活动变得稀疏，最终收敛于单一的表现形式。在图7A中，我们聚合了图6中所有物体和所有模块的细胞活动，以显示每次感觉后的平均细胞激活密度。当网络学习更多的对象时，初始密度和收敛时间会增加，因为网络为每个感官输入回忆更多的对象上的位置，并且它必须消除更多对象之间的歧义。

模型近似于理想观测器

理想情况下，网络应该在接收到与该物体唯一匹配的感觉运动序列时就能识别出该物体。在图7B中，我们比较了这种理想观测器的识别时间。理想的检测器在训练过程中存储特征及其相对位置，并在测试过程中根据存储的对象详细检查当前的感觉运动序列。只要物体是明确的，它就会产生一个正确的分类基于特征和相对位置的感知。我们还包括一袋功能模型。它忽略了位置信息，如果仅根据感官特征就能明确地确定对象，就能得到正确的分类。

该网络使用10个模块，数据集包含100个具有10个独特特征的对象。只有很少的物体可能由单一的感觉来决定，但三或四种感觉就足够了。随着每个模块中单元数的增加，模型的性能接近理想检测器的性能。每个模块有40 × 40个电池，两者几乎相同。特征包模型通常不能唯一地识别对象，因为许多对象是相同特征集的不同排列。

在接近模型容量极限时，识别时间下降

当这个模型学习更多的对象时，它最终开始比理想的观察者花费更长的时间来识别对象。当进一步推进时，它最终开始无法识别物体。在图7B中，每个模块有30 × 30个单元的网络需要比理想观察者更多的感觉来缩小目标，但它最终总是能识别出目标。每个模块有27 × 27个单元的网络在多次感知后往往无法识别目标，这表明网络已经超出了它的能力。

为了理解系统达到容量限制的方式，考虑当单个特征被感知时，位置模块中的激活密度。如果一个特征出现在多个位置，那么在学习过程中，位置层和感觉层会相互关联每个模块中的许多细胞与该特征。感知到这一特征将导致定位层中的大部分细胞被激活。如果这个百分比太高，那么不应该被激活的位置表示将大部分包含在这个密集激活中，从而导致
假阳性。在最坏的情况下，位置层将无法从这个感官输入中提取任何有用的东西，因为它将激活几乎所有的位置表示作为其密集激活的一部分。我们发现，影响模型识别时间的主要因素是模型是否接近其容量极限。在下一节中，我们将描述这个容量限制。

容量随定位层的大小、对象的统计而变化

之前的模拟研究了收敛到一个独特位置的时间。这里，我们考虑网络的容量与收敛时间无关。我们计算经过多次感觉后正确分类的对象的比例，并将容量定义为网络在保持90%准确率的情况下可以存储的对象的最大数量。虽然我们在这些模拟中每个对象使用10个位置，但位置的总数(对象的数量乘以每个对象的位置数量)才是最重要的。

值得注意的是，容量的这个定义是对模型识别对象能力的度量，而不仅仅是对其存储对象能力的度量。该网络可能会存储更多的物体预测模型，但在某一时刻之后，它将无法通过该模型的电路从感官输入中识别这些物体。该模型有多个潜在的瓶颈，可以决定这个突破点:感官特征的表征能力，位置的表征能力，细胞通过独立的树突片段学习的模式数量，以及网络同时表征多个位置的能力。通过以不同的方式改变模型参数和输入数据，这些都可能成为瓶颈，但我们发现，这些潜在瓶颈中最不可避免的是最后一个。

因为我们的实验关注的是相同的特征出现在多个物体上的场景，当感官输入导致位置层激活一个大到足以在感官层造成假阳性的表示组合时，模型开始遇到容量限制。当联合包含大量不应该是活动的位置表示时，就会发生这种情况。此事件发生的可能性受模型的模块数量、每个模块的单元格数量和对象的统计信息的影响。在图8中，我们描述了这些变量对模型容量的影响。

模型的容量随着模块数量的增加而增加，但收益递减。在图8A中，我们画了两条线来分析模块数量和容量之间的关系。顶部的线显示了拥有多个模块的影响，然后底部的线显示了这种影响是如何通过我们的模型的较低的树状阈值来减少的。即使使用单个模块，网络也能够聚合到一个位置表示上，用于相当数量的学习对象。然而，这种位置表示对对象来说并不是唯一的，所以这并不符合识别对象的条件;我们用一个红色的“x”来表示。添加更多的模块可以确保唯一的位置，并且每个额外的模块都有助于模型处理大型联合。当大量细胞处于活动状态时，它们防止模型出现过多的假阳性。更准确地说，对于每个表示，由于随机性而被激活的细胞的百分比将近似等于激活密度，有一些方差，拥有更多的模块可以减少这种方差。如果阈值是100%，那么模型可以通过添加模块无限地增加其容量。然而，为了避免依赖于每个神经元的可靠放电，该模型没有使用这么高的阈值。在我们的模型中，如果一个位置80%的细胞是活跃的，神经元就会检测到这个位置。在这个较低的阈值下，额外模块的好处渐行渐远，没有多少模块能够处理超过80%的激活密度。

之前对网格单元码的分析(Fiete et al.， 2008)表明，代码的表示能力随着模块的数量呈指数增长。这对于这个模型是成立的，但是这个模型的瓶颈不是它的唯一位置空间的大小。该模型的性能取决于它同时明确表示多个位置的能力。网格单元码的联合容量不随模块数量呈指数级增长。

模型的容量随每个模块的单元数线性增加(图8B)。当我们添加额外的单元格时，肿块的大小相对于单元格保持恒定，因此肿块相对于模块缩小。因为每个碰撞会激活模块中较小比例的单元，所以在网络达到物体分类开始失败的密度之前，模块可以激活更多的碰撞。

模型的容量随独特特征的数量线性增加(图8C)。这是因为它减少了每个特征的预期总出现次数，从而减少了每个联合中的元素数量。这表明世界的统计数据会影响模型的容量，这也意味着这个网络可以通过调整从感官输入中提取的“特征”来提高它的容量。

由于后两个参数与容量之间具有独立的线性关系，因此可以相互补偿。在图8D中，我们绘制了一个有10个模块的网络中的对象容量。我们表明，通过相同的因素增加(减少)每个模块的单元数和减少(增加)惟一特征的数量会使容量大致保持不变。这可以通过图表对角线上的近似对称来说明。

如果对象至少有一个足够不常见的特征，该模型就能识别该对象

到目前为止，我们已经描述了这个模型识别对象的能力:“如果网络学习的对象总数少于c个，那么网络将可靠地识别一个对象，”我们测量了c。这个描述建立在对对象的许多假设之上。我们希望能够以一种不特定于这些假设的方式来描述模型。

考虑到模型识别物体的能力取决于感官特征所唤起的细胞活动的密度，我们发现我们可以更直接地描述模型的性能，回答:“如果对象包含在所有学习对象中出现次数少于k次的特征，那么网络将可靠地识别一个对象。”在另一组实验中(补充图S1)，我们使用多个交替分布的特征生成对象。我们发现，网络的断裂点相对于c(学习对象的数量)确实随着特征分布的选择而有很大的变化，而它的断裂点相对于k(通过感知一个特征回忆的位置的数量)在分布中更一致。这表明网络相对于k的性能在现实世界的统计数据中是成立的。使用这两个指标c和k，我们在图9中总结了所有这些结果。

我们得出的结论是，如果对象至少有一个足够不常见的特征，这个特征可以使网络回忆起足够少的位置，那么该模型就可以可靠地识别出该对象。在感知到这个特征之后，模型可以使用其他更常见的特征来完成对对象的识别，但它需要一些初始线索来帮助它激活一个可管理的联合，然后它可以缩小该联合。有了足够多的细胞，这个初始线索并不需要特别独特。例如，如果模块每个模块有10 × 10个单元格和10个模块，那么该功能可以有10个学习到的对象上的位置，如图9所示，这个断点可以通过添加更多单元格而任意提高。该网络还可以通过调整从感官输入中提取的“特征”集来避免碰到这个断点。

映射到生物学

我们已经描述了一个感觉运动推理的两层网络模型，现在考虑这个网络主题如何映射到已知的皮质解剖和生理学。第四层(L4)被认为是丘脑皮层感觉输入的主要目标(Jones, 1998;道格拉斯和马丁，2004年;他们耶尔等人，2010)。这些连接被认为是驱动输入(Viaene et al.， 2011)，并针对兴奋性和抑制性神经元，抑制性神经元有轻微延迟，为神经元提供了激活的机会窗口(Harris和Shepherd, 2015)。Mountcastle(1957)将神经元组织成具有共享接受野的小柱(Buxhoeveden, 2002)。

L4和第6a层(L6a)之间的连接与我们模型中的连接非常相似(图3，箭头2和4)。丘脑输入在L4突触中所占比例相对较小;大约45%的突触来自L6a (Binzegger et al.， 2004)。L6a的连接很弱(Kim et al.， 2014;哈里斯和谢泼德，2015年)。它们连接到L4细胞的远端树突段，而丘脑皮层传入束则更近端连接(Ahmed et al.， 1994;Binzegger et al.， 2004)。L4细胞也与L6a细胞形成大量连接(Binzegger et al.， 2004)。这些生物学细节与我们的网络模型非常吻合，其中位置层(假定为L6a)对感觉输入层(假定为L4)有调节影响，而感觉输入层反过来又能驱动位置层的表征。

我们的定位层还需要一个电机输入。实验表明，运动区(如M2)的L5细胞投射到感觉区，包括第6层(Nelson et al.， 2013;Leinweber et al.， 2017)。小鼠V1第6层的主要细胞从脾后皮质直接接收投影，信号头部水平旋转的角速度(Vélez-Fort et al.， 2018)。也有一个潜在的间接途径，通过丘脑皮层输入，目标6层(Thomson, 2010;哈里斯和谢泼德，2015年)。丘脑中继细胞从第5层神经元接收输入，这些输入被认为是皮层下发送的运动命令的传出副本(Chevalier和Deniau, 1990;琼斯,1998)。这些直接或间接的通路都可以作为L6中通路整合的运动信号。

我们的模型从网格中汲取灵感，将细胞系统置于海马结构中。我们的位置层是以网格单元格为模型的。这些细胞投射(Zhang et al.， 2013)在海马体中放置细胞(O 'Keefe and Dostrovsky, 1971)。海马体中含有位置细胞的区域也投射回内嗅皮层中含有网格细胞的区域(Rowland et al.， 2013)。许多位置细胞似乎代表项目-位置对，这些对是通过经验学习的(Komorowski等人，2009年)，这一现象类似于我们感觉层的特征-位置对的学习。

新皮层中类似网格细胞的位置表示是推测的，但初步的实验支持了新皮层中网格样编码。让人类执行任务的功能磁共振成像实验已经导致前额皮质的活动信号类似于网格细胞信号(Constantinescu et al.， 2016;Julian等人，2018a)。直接细胞记录也显示了额叶皮层的网格状活动(Doeller et al.， 2010;Jacobs et al.， 2013)。这些实验与假设相一致，网格状细胞存在于新皮层中，而不仅仅是海马形成的一种现象。这些网格细胞是在寻找海马结构中与网格细胞反应相似的细胞时发现的;在“可测试的预测”部分，我们预测通过寻找表示传感器相对于物体位置的单元，将会发现更多类似网格的单元。

在我们的模型中，初级感觉皮层代表在一个外部参考系的位置上的感觉输入。这与Saleem等人(2018)的结果一致。当老鼠在一条虚拟的轨道上奔跑时，初级视觉皮层中大部分被记录的细胞会对动物在轨道上的位置进行编码，即使当老鼠在轨道上的多个点上收到视觉输入时也是如此。根据我们的模型，在这个任务中，视觉皮层表示一个传感器(鼠标的眼睛)相对于一个物体(虚拟轨迹)的位置，并且皮质使用视觉输入来回忆轨迹上的位置，同时使用鼠标的移动来更新这些位置表示。他们发现V1的位置表示中的错误与CA1的位置表示中的错误相匹配，这表明这两个区域使用相同的路径积分信号。

虽然还需要进一步的实验工作，但有证据表明，L4和L6a分别为我们的感觉层和位置层提供了最佳的候选种群。

讨论

提出了一种用于感觉运动目标识别的双层神经网络模型。通过将感官输入与以对象为中心的位置表示相结合，该模型将对象学习为感官特征的空间排列。物体学习和物体识别都独立于运动和感觉的特定顺序。

该模型的定位层包含与内侧内嗅皮层网格细胞模块类似的模块。位置模块表示对象参考框架中感知到的位置。位置模块接收更新和预测新位置的移动输入。感觉层将位置的表示与感觉输入结合起来，以创建对对象和这些对象上的位置独特的感觉输入表示。

在我们的模型中，物体识别是通过一系列的感觉和动作进行的。感官输入激活了之前学习过输入的一系列位置。定位层根据电机输入更新这些位置。更新的位置在感觉层引起预测。下一个感官输入缩小了可能的位置和可能的物体。通过这种方式，一系列的感觉和动作将允许模型快速推断出被感知到的对象。

该模型提供了我们早期模型(Hawkins et al.， 2017)中引入的位置信号的具体实现，并提出了一种感官输入和运动输入如何协同工作的机制。

网格单元模块是否支持联合

在我们的模型中，我们将网格单元格模块视为具有众所周知和先前记录的属性的黑盒子。我们的模型对于创建网格单元属性的内部动态和机制是不可知的。但是，我们为网格单元格模块提供了一个通常在网格单元格中没有注意到的附加属性:支持联合。我们模型中的网格单元模块可以同时激活、维护和转移多个活动凸起。已经假设并观察到皮质板上的多个活动凸起(Burak和Fiete, 2009;Gu et al.， 2018)，但在这些情况下，凸点具有相同的空间相位;当按菱形排序时(图1B)，那些同时活跃的细胞将被分组在一起，因此肿块将显示为单个肿块。在我们的模型中，当位置不明确时，即使在已排序的菱形中也会出现多个凸点。可以将网格单元动态的各种模型插入到该模型中，但是union属性为这些模型引入了新的要求。

已经提出了几个模型来解释网格单元动力学(Giocomo等人，2011年)。循环网格单元模型得到了更多的经验支持(Yoon et al.， 2013)，而网格单元模型建立了各自独立的响应。在循环模型中，网格细胞通过速度输入和与其他网格细胞的连接(直接或通过中间神经元)来确定它们的活动。一个著名的循环模型是连续吸引子网络(Fuhs和Touretzky, 2006;Burak和Fiete, 2009)，它执行了鲁棒路径集成，并为六边形发射场的起源提供了一个简单的解释。对于这些字段的起源的另一种解释是，它们是一种最佳的位置代码，由神经学习规则自然学习。这一论点出现在两方面的研究中。在路径集成模型中，Banino等人(2018)和Cueva和Wei(2018)发现，经过训练执行路径集成的循环神经网络会自然地发展网格细胞，尽管这两种网络都没有报告在每个尺度上发展网格细胞的完整菱形。不考虑路径集成，Kropff和Treves(2008)、Dordek等人(2016)和Stachenfeld等人(2017)表明，对位置细胞活动进行Hebbian学习的细胞自然会学习与网格细胞类似的周期性放电场。

连续吸引子模型之所以如此命名，是因为它具有连续的稳定状态流形。如果网络激活的表示不在这个稳定表示的集合中，那么该活动将移动到最近的稳定状态。在典型的连续吸引子网络中，一个集合不是一个稳定的状态，网络会将多个碰撞的集合坍缩为单个碰撞。是否可能有一个具有稳定联盟态的连续吸引子是一个悬而未决的问题。在本文中，我们证明了网格单元格模块与联合工作在理论上是有利的。吸引子动态之所以吸引人，部分原因是它们解释了六边形发射场，但正如前面提到的，这些可能是循环神经网络学习位置代码的自然结果。

定位层的内部机制建模是未来研究的一个领域。可能有替代的神经机制来实现联合的计算等效，例如跨时间交错不同的表示，就像在单个感觉神经元代表多个同时刺激中观察到的那样(Caruso等人，2018年)。

以自我为中心 vs 以对象为中心坐标

像眼睛和皮肤这样的传感器在以观察者为中心或以自我为中心的坐标框架中检测特征。在自我中心坐标中学习物体的特征是低效的，因为系统需要学习物体在每一个移动的位置和旋转的方向。我们的模型使用网格细胞样模块表示位置，就像内嗅皮层中的网格细胞一样，皮质网格细胞表示相对于被观察的外部物体的位置。

因此，从以自我为中心的参考系转换为以对象为中心的参考系是必要的。如果参考系是基于笛卡尔坐标的，那么就有必要建立原点，正如Marr和Nishihara(1978)所概述的那样，转换是复杂的。网格单元格表示避免了这种复杂性。基于网格单元格的参考系没有原点。网格单元格表示位置之间的相对关系，而不是与原点的相对关系。

然而，用网格单元表示对象仍然需要知道传感器的方向和相对于对象的特征。我们的模型还没有方向的表示。因此，我们的模型只会识别一个对象，如果对象是在它的学习方向相对于传感器。我们的模型的扩展版本可以使用与头向细胞类似的方向(Taube et al.， 1990)。网格细胞表示动物在认知地图上的位置，而头向细胞表示动物相对于认知地图的方向。当动物移动时，网格细胞模块根据动物的方向移动它们的活动碰撞。类似地，我们期望新皮层能够表示传感器相对于被感知对象的参考框架的方向，而这个方向将影响传感器的运动如何转化为皮层网格细胞模块中凸起的运动。这个扩展模型将能够学习定向和不变的对象模型，并处理传感器相对于对象旋转。

2D vs. 3D对象

我们已经用二维网格单元模块描述了我们的模型来学习二维对象，然而，新皮层有能力学习3D对象。如果位置代码表示相对于对象的3D位置，我们的模型应该与3D对象一起工作。内嗅皮层如何代表3D空间是一个活跃的研究领域(Jeffery et al.， 2015)。我们的团队目前正在扩展我们的模型，以包括3D表示和方向。

与其他模型的关系

我们的模型利用感官特征的相对位置来识别物体。随着时间的推移，物体通过连续的感觉和运动被消除了歧义。相比之下，大多数现有的物体识别模型涉及一个严格前馈的空间层次系统(Riesenhuber和Poggio, 1999;Serre等人，2007;Yau et al.， 2009;DiCarlo等人，2012)。在这些模型中，每一层并行地检测越来越抽象的特征，直到在层次结构的顶部识别出一个完整的对象。我们的模型表明，层次结构的每一层可能比之前假设的更强大。在Hawkins等人(2017)中，我们讨论了空间分离的感官输入(跨越多个皮层列，每个列计算一个位置信号)如何并行合作识别对象，以及对层次的一些含义。我们的模型为将感觉运动行为整合到一个层次系统中提供了一条路径，并解释了许多不能用纯前馈模型解释的皮质间和皮质内连接。将我们的模型整合到一个完整的层次系统中是未来研究的一个主题。

在熟练运动行为的背景下，有关于感觉运动整合和内部模型学习的重要文献(Wolpert和Ghahramani, 2000;Wolpert et al.， 2011)。这些课程主要集中在学习电机动力学和运动学控制，包括到达和抓取任务。我们的模型侧重于更结构化的对象识别范式，但与这一文献体系有许多高层次的相似之处。我们的定位层与电机控制中的正向模型高度相似(Wolpert等人，2011年)。在这两种情况下，使用电机传出副本更新当前状态以计算下一个状态。在这两个模型中，这都是对状态的估计，用于预测(图3中的箭头2)，然后与感官输入结合产生当前状态(图3中的箭头3和4)。主要的区别是，我们的模型识别的是一组结构化对象，而不是运动轨迹。神经机制也有显著不同。然而，有趣的是，同样的想法可以应用于这两种情况，并可能反映出大脑中更普遍的设计模式。深入探讨这种关系是未来研究的课题。

我们的模型为视觉皮层的预测加工提供了另一种解释。现有的视动重映射模型表明，它是通过在视觉皮层中移动图像的参与部分来发生的(Wurtz, 2008)。这种解释需要视网膜位图的每个部分都与其他每个部分连接，要么是水平连接，要么是通过前馈输入，它需要使用眼动信息来实现这些连接的一小部分。在我们的模型中，视觉皮层的每个小块计算视网膜的一个小块相对于被关注对象的位置，然后利用这个位置预测感官输入。当眼睛扫视静态物体时，我们的模型不需要视觉皮层内的任何信息水平移动。因此，本文提出了一种不需要视觉皮层的每个小块通过长距离连接与其他小块联系在一起的视动重映射模型。实现该扩展模型是未来研究的一个课题。

最近的一篇文章(Keller和Mrsic-Flogel, 2018)提出了一种使用信号形成预测和表示预测误差的神经电路。这是一个通用电路，可以使用任何类型的预测信号。在目前的研究中，我们提出了一种特殊类型的预测信号-位置-以及它们是如何更新的。我们将该信号与一种不同的神经机制相结合进行预测(Hawkins和Ahmad, 2016)，但也可以使用Keller和mrsci - flogel的机制将位置作为预测信号。这两种机制的不同之处在于它们如何表示预测误差。在我们的模型中，当输入与预测相匹配时，网络在这个特定的上下文中激活输入的稀疏表示，而不匹配则导致网络在许多不同可能的上下文中激活输入的密集表示。Keller和Mrsic-Flogel的模型用两种不同的细胞群表示感官刺激和预测误差。

其他人强调了感觉运动处理在我们如何以不同的方式感知不同的感觉形态方面的重要性。O 'Regan和Noë(2001)使用了拿着一个瓶子和看到一个瓶子的例子。他们提出，你通过感官形态对瓶子的有意识感知来自于你对这种形态的掌握，来自于你能够预测当你在瓶子上移动你的手时会有什么感觉，或者当你在瓶子上移动你的眼睛时会看到什么。在这篇论文中，我们没有关注意识知觉，但我们的模型确实提出了大脑如何用不同的感觉模式来表示瓶子，从而对运动做出预测。我们认为特定于对象的位置表示的想法与这种感知的观点是相当兼容的。

我们实验室最近的一篇文章(Hawkins等人，2019年)提出了一个基于位置的框架来理解新皮层。在那里，我们描述了对象模型如何通过表示网格单元格之间的位移来相互关联，从而支持组合对象的表示。在本文中，我们提供了一种学习对象模型的神经机制，以适应这种合成方法。这是一个更大的理论的一个基石，在这个理论中，位置是新皮层的关键计算基础。

可测试的预测

我们的模型做出了许多可以通过实验验证的预测。我们扩展了Hawkins等人(2017)的预测。

(1)新皮层使用网格细胞模块的类似物来表示相对于物体的位置。模块中的单元活动在多个表示中移动，因为所关注的位置相对于对象移动。例如，在体感区，当动物的手指相对于被关注的物体处于特定位置时，细胞会有选择性地做出反应。就像内部网格单元格模块对每个环境使用相同的映射一样，单个模块的单元格对每个对象使用相同的表示集合。这个地图的大小有限，因此它将在其边缘执行某种形式的包装。

(2)新皮层使用多个模块的种群编码来表示特定物体的位置。

(3)这些模块位于新大脑皮层的第6层。

(4)从第6层到第4层的投射调节了第4层中哪些细胞激活。如果第6层的输入被实验抑制，第4层的活动将变得更加密集。

(5)从第4层到第6层的连接可以驱动第6层细胞变得活跃，但这只发生在动物接收到一个不可预测的输入时。

模型的细节

每个模块有固定数量的单元，每个单元在菱形中有固定的相位。活动的高斯凸块在这些细胞上移动，为每个细胞分配一个内部标量激活。当细胞内部的这种激活超过阈值时，细胞就会激活。在本节中，我们将详细介绍这些计算。

每个模块包含w×w单元格。每个细胞c有一个恒定的相位${\varphi }_c$。我们将2D范围[0,1)×[0,1)划分为w×w个面积相等的范围，并将每个单元格的${\varphi }_c$设为其中一个范围的中心。因为这些模块使用由60◦[Eq.(3)]分离的基向量，当映射到物理空间时，这些细胞形成菱形，他们在一个六角形打包在一起。

由凸块b引起的细胞c的内部标量激活，记为$a_{c,b}$，等于它们之间距离的高斯值:

距离(${\varphi }_c$， ${\varphi }_b$)表示相菱形上晶胞与凸点之间的最短距离。计算这个距离需要改变基础，使每个$\varphi$都是菱形上的一点，而不是[0,1)×[0,1)正方形上的点。σ表示凸起相对于菱形的大小，我们稍后讨论。

当有多个凸块时，来自每个凸块的标量激活被组合起来，就好像每个激活状态编码一个事件的概率一样。组合标量激活编码了这些事件的“或”的概率:
为了计算模块i的活动单元$A_t^{loc,i}$，我们计算每个单元的标量激活，并检查它是否高于阈值$a_{active}$:
![在这里插入图片描述](https://img-blog.csdnimg.cn/7aa3bc5d187e4b0cb267ed1fe538d16d.png

我们使用网格单元模型中常见的读出分辨率参数$\delta \phi$来选择$a_{active}$ (Fiete et al.， 2008;Sreenivasan和Fiete, 2011)如下:

读出分辨率$\delta \phi$近似地指定了凸包编码的相位范围的直径。因为模块是2D的，如果读出分辨率是1/4，那么凸起可以编码菱形中大约16个可能的位置。$2/\sqrt{3}$的乘因子解释了这样一个事实:当圆以六边形的形式聚集在一起时，它们会留下一些未覆盖的区域;这个因子使圆重叠并覆盖这个区域。在一个单一的碰撞中，改变$\sigma$参数对模型没有影响，因为$\delta \phi$参数完全控制了细胞被认为是活性的比例。当有多个凸起时，$\sigma$变得相关。这些肿块越宽，它们结合的越多，并导致间质细胞的标量激活上升到$a_{active}$ 以上。

我们改变$\sigma$和$\delta \phi$如下。我们的基线参数模拟了大鼠内嗅网格细胞模块的稀疏性。我们将$\sigma$设为0.18172，该数值是通过将二维高斯拟合到模型在Monaco和Abbott(2011)生成的发射场中得到的。我们将$\delta \phi$设为1/3的保守估计值。在这种配置中，我们为网络分配6 × 6个细胞，而一个bump总是激活至少2 × 2个细胞。当我们测试有更多单元格的网络时，我们假设肿块相对于单元格保持固定的大小，即肿块相对于模块的大小更小，我们相应地缩小$\sigma$和$\delta \phi$。例如，对于12 × 12单元格，我们使用$\sigma /2$和$\delta \phi /2$。通过以这种方式改变参数，单个肿块总是激活4到7个细胞，这取决于肿块的中心位置相对于它的局部邻近细胞，当我们改变细胞数量时，我们就有效地改变了肿块不激活的细胞数量。

在学习过程中，只有具有最高标量激活的细胞与感知特征相关联[当一个感知特征激活一个细胞时，它通过式(7)激活以细胞为中心的凸起，激活它周围的细胞]。这意味着该模型的学习分辨率是读出分辨率的两倍。因为感觉特征与代表一系列相位的细胞相关联，所以感觉输入回忆的相位总是有一些不确定性。如果学习到的分辨率并不比读出分辨率更精确，那么活动细胞的碰撞就需要扩大，以解释这种不确定性，有效读出分辨率将只有一半的精确度。使用固定大小的凸点，实现特定的读出分辨率——也就是说，让凸点编码具有特定直径的一系列相位——要求学习分辨率至少是该读出分辨率的两倍。

图7B中的理想分类器将所有对象存储为2D数组。在推理过程中，它使用第一个感知到的特征在所有具有该特征的对象上找到所有可能的位置，并将这些位置存储为候选位置。随着每个后续移动，它会更新所有候选位置。任何更新的候选对象，如果不是对象上的有效位置，或包含与新感知的特征不匹配的特征，都将从候选列表中删除。一旦只剩下一个位置，推断就成功完成了。

特征检测器包为每个学习对象存储一组特征。它不记录特征出现的次数，只记录出现在物体某处的一组独特特征。在推断过程中，另一组记录到目前为止已经感知到的特征。一旦只有一个对象包含所有感知到的特征，推理就成功完成了。如果在被测试对象上的所有位置都访问过之后，有多个对象包含所有特征，那么该对象就不能唯一分类。

递归动力学

该网络包含一个循环循环，因此在给定时间步的第4阶段之后，有可能出现额外的循环动态。然而，由于第二阶段的输入是调节的，从来没有驱动细胞变得活跃，网络一般在第四阶段之后收敛。我们发现，模拟这些动态偶尔可以让网络识别对象少一个感觉。为了保持模型和表示法的简单性，本文在阶段4之后将模拟推进到下一个时间步，阶段1与下一个感官输入重复。

作者贡献

ML和JH构想了整个理论。ML, JH, SP和SA构想了神经科学的详细映射并撰写了手稿。ML、SP和SA帮助设计了模拟。ML和SP进行了仿真。ML和SA创建了算法的详细公式。

资金

Numenta是一家私人控股公司。它的资金来源是独立的投资者和风险投资家。

致谢

我们感谢审稿人提供的有帮助和建设性的反馈。我们感谢Mirko Klukas和Numenta的许多其他合作者多年来进行的许多讨论。

补充材料

本文的补充材料可以在网上找到： https://www.frontiersin.org/articles/10.3389/fncir.2019.00022/full#supplementary-material

图S1 |改变对象统计，模型的断点相对于学习到的对象的数量变化显著。断点相对于物体特征所唤起的位置数量更为一致。在这些图表中，我们使用单一模型，并对6种不同的对象分布进行测试。该模型使用10个模块，每个模块10 × 10单元。(左)网络的容量取决于对象的统计。当出现一定数量的对象后，网络的性能就会开始崩溃，而这个崩溃点会因对象分布的不同而发生数量级的变化。(右)当用“一种感觉回忆起的位置的数量”而不是“学习到的物体的数量”来描述时，这个断点的变化明显要小得多。使用第一个图表中的相同数据，对于每个物体，我们测量该物体最罕见特征出现的总次数，并根据这个数字绘制识别精度图。对于每一个这样的对象分布，当被召回位置的数量在一个小的区间内(保守地说，在7到15之间)时，模型达到了它的断点。由于对象的其他特征(不仅仅是其最稀有特征)的统计，仍然有一些变化，但最稀有特征的出现次数为网络是否能识别该对象提供了一个很好的第一近似。(对象描述)。每个对象集有100个独特的特征，每个对象有10个特征，除非另有说明。前三组使用与所有其他模拟相同的策略生成对象，只是改变了参数。后三种使用不同的策略。对象集1:baseline。对象集2:40个独特特征而不是100个。对象集合3:每个对象有5个特征，而不是10个。对象集合4:每个特征出现的次数相同(±1)，而不是每个对象都是随机选择的特征集合。对象集5:特征的双峰分布，概率。将功能划分为两个大小相等的池，从第二个池中选择功能的次数要多于从第一个池中选择功能的次数。对象组6:特征的双峰分布，强制结构。这些特性被平均地划分到池中。每个对象由第一个池中的一个特性和第二个池中的九个特性组成。

参考文献

Ahmad, S., and Hawkins, J. (2016). How do neurons operate on sparse distributed representations? A mathematical theory of sparsity, neurons and active dendrites. arXiv:1601.00720 [Preprint].

…
…