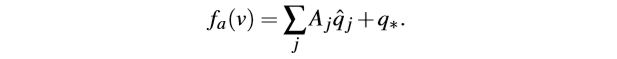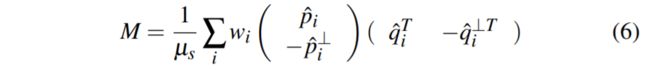利用MLS移动最小二乘法对图像变形
这是我的【项目笔记】利用OpenCV的MLS图像扭曲变形实现中的第一部分
本文主要对MLS进行了一定讲解
先简单了解一下什么是最小二乘法
最小二乘法
当我们在测量某个值y时,由于误差的存在,可能多次测量的结果不尽相同
我们把多次测量得到的不同结果yi画在同一坐标系中
同时将猜测的实际值y也画在坐标系中
![]()
每个yi和y都有一个差值| y - yi |,称为误差
记所有误差的平方和
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1Pc3Ah3Q-1573289354246)(https://i.loli.net/2019/11/07/YhmLJkTn5yAIRo9.png)]
由于实际值y是我们猜测的,所以它的值可以变化,同时误差的平方和ε也会随之改变
![]()
于是高斯或是法国科学家勒让德就提出使误差的平方和最小的 y 就是真值,这是基于,如果误差是随机的,应该围绕真值上下波动
这就是最小二乘法,即
此外,经证明得出误差的分布服从正态分布(不愧是天下第一分布),这里就不证明了
总的来说,对于被选择的参数,应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为:
最小化问题的精度,依赖于所选择的函数模型
移动最小二乘法
移动最小二乘法与传统的最小二乘法相比,有两个比较大的改进:
- 拟合函数的建立不同。这种方法建立拟合函数不是采用传统的多项式或其它函数,而是由一个系数向量
a(x)和基函数p(x)构成, 这里a(x)不是常数,而是坐标 x 的函数。- 引入紧支( Compact Support)概念。认为点
x处的值y只受 x附近子域内节点影响,这个子域称作点x的影响区域, 影响区域外的节点对x的取值没有影响。在影响区域上定义一个权函数w(x),如果权函数在整个区域取为常数,就得到传统的最小二乘法。
节选自《基于移动最小二乘法的曲线曲面拟合-曾清红》
利用MLS变换图像
这一部分,我主要参考了论文《Image Deformation Using Moving Least Squares》中的内容
考虑由用户设定锚点来对图像变形进行控制的情况,首先进行准备工作,推导出公式
准备工作
设p为一组控制点,q是它对应的变形位置
对于图像中的某一点v,有最小的仿射变换lv(x),使
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ev2juMRP-1573289354248)(https://i.loli.net/2019/11/07/ri2nCqNtg7s9aAO.png)]
成立。其中pi和qi是行向量,权值wi满足
各点权重wi
由于对于每个v都有不同的wi的值,称之为移动最小二乘最小化(a Moving Least Squares minimization)。对于每个v都有不同的lv(x)
此时定义变形函数f(x) = lv(x),可见当v接近pi时,wi趋于无穷、f(pi) = qi,此外若qi = pi,则lv(x) = x、f(v) = v
由于lv(x)是一个仿射变换,由线性变换矩阵M和偏移量T组成,即
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qgipx00F-1573289354250)(https://i.loli.net/2019/11/07/5TFtSdsc87HKMBi.png)]
又可根据M求T,即
偏移量T
其中
因此,lv(x)可以改写为
仿射变换lv(x)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UTsiSVbM-1573289354255)(https://i.loli.net/2019/11/07/qwJ21uI64SY8Drt.png)]
于是方程(1)中的最小二乘问题又可以重写为
最小二乘
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BHj6tzgy-1573289354259)(https://i.loli.net/2019/11/07/ISw9Ayq7Jp6b4Zo.png)]
其中ˆpi = pi − p∗且ˆqi = qi −q∗.
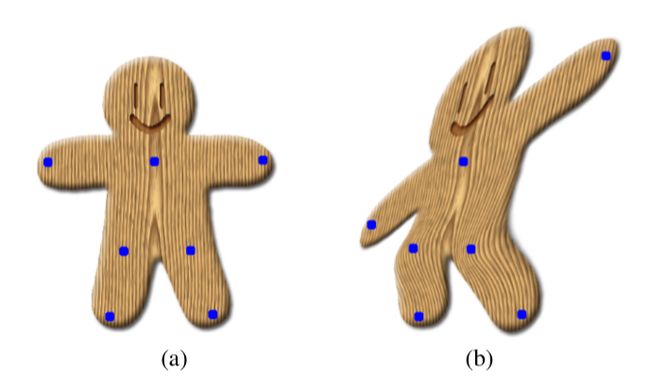
可以发现,我们要进行的图像变形最终效果与变换矩阵M相关联,因此根据矩阵M的不同,可以获得不同效果的变形。论文中将其分为了仿射变换、相似变换和刚性变换
在这里仅呈现了每种变换对应的变化矩阵和变化函数,具体推导可以参见论文原文
仿射变换
找到使方程(4)最小的矩阵M如下
仿射变换矩阵
由此得到的变换函数如下
变换函数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-simXV0Fo-1573289354261)(https://i.loli.net/2019/11/07/b6Q3OvVD42pewag.png)]
也可以写为
其中
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F7W3GCxo-1573289354263)(https://i.loli.net/2019/11/07/kwrxCagRHdK5qI6.png)]
可见,一旦给定了某个点v,此处的Aj便可以提前计算得出
如图b是仿射变换的效果图
相似变换
得到进行相似变换时的变换矩阵M为
相似变换矩阵
其中
由此得出变换函数
变换函数
其中可以提前计算的部分
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nm6xxsRs-1573289354267)(https://i.loli.net/2019/11/09/U1TcvDLV4aYkWf7.png)]
如图c是相似变换的效果图
刚性变换
刚性变换的矩阵形式与相似变化相同,仅是其中的参数miu发生了变化
刚性变换矩阵
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IeVTnfXA-1573289354268)(https://i.loli.net/2019/11/09/1YbZlwnScva42CB.png)]
其中
得出刚性变化的变化函数为
变换函数
下图中d即刚性变换的效果
参考文献:
《Image Deformation Using Moving Least Squares》
《基于移动最小二乘法的曲线曲面拟合》
参考博客:
如何理解最小二乘法?–马同学