时间序列学习（5）：ARMA模型定阶（AIC、BIC准则、Ljung-Box检验）

第3篇笔记给出了一个较为复杂的模型ARMA，它是AR和MA模型的组合。

如果要用ARMA模型对时间序列进行建模，那么首先得确定模型的AR和MA两部分的阶数$(p,q)$；确定好阶数后，我们就可以通过回归或者简单的最小二乘法来进一步确定模型的参数。

所以，首先我们得确定模型的阶数。

确定阶数其实可以直接从前面介绍的相关图中通过“截尾”及“拖尾”获得（这个方法不详述了）。不过看图形判断毕竟有点主观，下面介绍基于信息量准则的方法。

1、信息量准则

很显然，当ARMA模型的阶数越高，其描述对象样本的能力就越强。但是阶数越高，参数也就越多，容易造成过拟合的现象。因此我们需要找一个度量工具，来确定最佳的阶数。

用的较为广泛的工具为赤池信息量准则（Akaike information criterion，简称AIC）以及贝叶斯信息量准则（Bayesian information criterion，简称BIC）。

令$L$是模型参数的似然函数，它是一个概率函数（具体细节不给出了），读者们可以这样理解：给定模型的一组参数，似然函数描述的是在这组参数下得到样本数据的概率。

很显然，当似然函数越大，给定参数对模型的描述越准确。那么，对于较大的阶数，似然函数肯定也较大。

AIC准则与BIC准则就是对似然函数与参数个数的权衡。我们既希望似然函数越大，又希望参数个数越少。

令$k$为参数个数，下面就是AIC和BIC的定义：

$$AIC=-2\ln (L)+2k$$
$$BIC=-2\ln (L)+k\ln (n)$$

上述$n$是序列宽度。当阶数$p,q$增加，$2\ln (L)$会变大，但同时$2k$也会变大。所以AIC和BIC存在一个最优值。

我们在寻找最佳阶数的时候，就是寻找使得AIC和BIC取最大值的阶数$(p^{\ast },q^{\ast })$。

2、寻找对数收益率序列的最佳阶数

我们对沪深300于2018年1月1日至2019年12月13日的日对数收益率序列（这是本系列笔记一直用的例子）寻找AIC和BIC准则下最佳阶数。

import statsmodels.tsa.stattools as st
from statsmodels.tsa.arima_model import ARMA

# return_df见下面的[研究]部分
order_analyze = st.arma_order_select_ic(return_df, max_ar=5, max_ma=5, ic=['aic', 'bic'])

这里，我们指定了所考察的AR和MA的最大阶数分别为5。

打印结果看看（tuple类型）。

order_analyze.aic_min_order

(1,3)

order_analyze.bic_min_order

(0,0)

可以看到，AIC和BIC准则给出的结果不一样。BIC直接将序列看成是纯的白噪声了。

3、构建模型

确定了阶数后，我们就构建出了模型，模型中的参数可以采用极大似然估计、最小二乘法或者机器学习的方法拟合出来。

假如我们用(1,3)阶来构建，statsmodels中的操作如下：

from statsmodels.tsa.arima_model import ARMA

arma_model = ARMA(return_df, (1,3))
fitted = arma_model.fit()

此时程序报错了。上述拟合默认采用MLE（极大似然估计）对参数进行估计。报错原因是参数计算过程无法收敛。这其实说明阶数(1,3)的ARMA模型拟合给定数据平稳性不够。这也从另一方面说明了，信息准则只是一种度量，而不是充分条件。

我于是手动降低了阶数，改成(1,1)阶。

from statsmodels.tsa.arima_model import ARMA

arma_model = ARMA(return_df, (1,1))
fitted = arma_model.fit()

此时参数求解过程可以收敛。我们用下面的方法获得模型预测出的同时段的序列：

predict_results = fitted.predict()

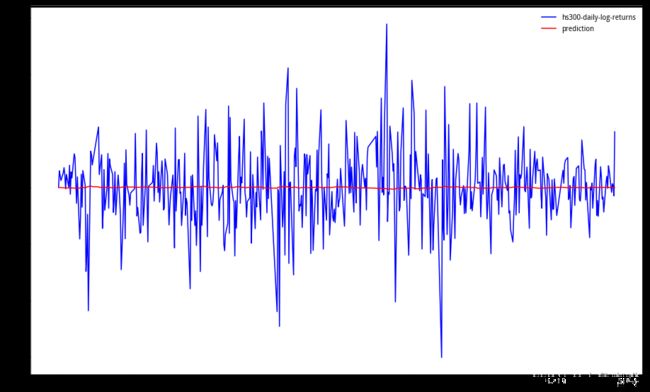
将预测序列与原始序列放在一起看看：

可以看到低阶模型只捕捉到了均值，波动或者周期性的信息没有被学习到。

另一方面，对数收益率序列对于(1,3)阶来说不太平稳，那么进一步看看其差分序列呢？其差分序列可以通过下面的方式获得：

return_diff = return_df.diff()   # 注意，首项为NaN

这个序列用AIC准则还是获得了(1,3)阶的最佳阶数，而且回归时可以收敛。

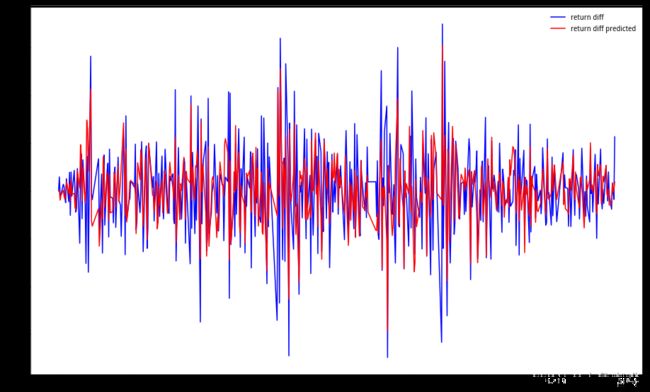
我们看看数收益率的差分序列及其(1,3)阶ARMA模型预测序列的拟合度如何？

可以看到，拟合效果还是不错的。不过，这里不排除过拟合的原因。另外差分序列对实际的指导作用也不强。

下面看看模型怎么做进一步评估。

4、模型评估

上一节用$ARMA(1,1)$对对数收益率序列进行了建模。通过对比原始序列以及预测序列，发现其效果不好。有没有什么更加严格的方法来检验模型效果好不好呢？

这里经常采用的检验方式叫Ljung-Box检验（LB检验），这是一种用来检验是否为白噪声的检验方式。这种方法基于自相关系数以及样本数构建了一个服从卡方分布的统计量用于检验（具体细节不详述了）。

如何利用Ljung-Box检验呢？我们通过所构建的ARMA模型实际上得到了一个新的序列（就是上面的预测序列），如果模型对原始序列解释性很好，那么这个新的序列与原始序列的差值（残差序列）应该是白噪声序列。

残差序列通过下面的方式获得：

fitted.resid

fitted是我们拟合出来的模型。

Ljung-Box检验的原假设（H0）是数据是独立的，总体相关系数为0，也就是白噪声；备择假设（H1）是原数据不独立，存在相关性。

我们用下面的代码进行检验：

acorr_ljungbox(D_data, lags=10)

结果如下：

(array([0.06917427367572804, 0.10977624497632564, 7.163542412123143,
        10.5181200037471, 11.04100847323994, 13.984160530490588,
        17.313146495753983, 18.38263375000973, 20.371510136523654,
        21.397478408429066]),
 array([0.7925428516146076, 0.9465910442804261, 0.06686382432745534,
        0.032548304932769556, 0.050572941411398446, 0.029813600858776174,
        0.015484799161404003, 0.018533813479289844, 0.015753105270723704,
        0.01848623388067896]))

函数中的lags是我们要查看的最大时间间隔（或者叫滞后阶数）。结果中第一个array列是LB检验统计量，第二个array列是LB-p-Value值。

我们看到p-Value没有显著小于1%的，所以我们无法拒绝原假设。此时可以接受残差序列是白噪声。进一步地，可以认为模型对原始数据是有解释性的。

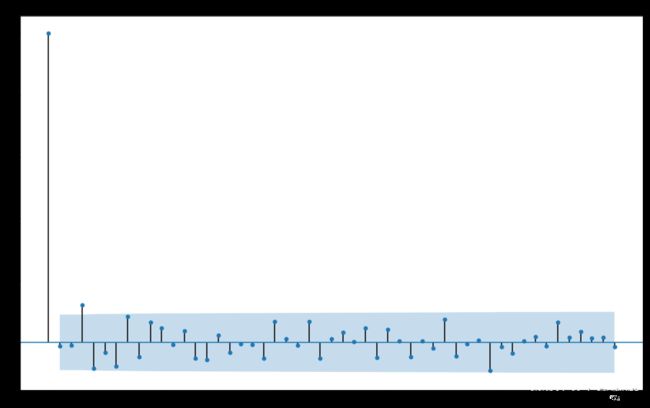
我们看看下面残差序列的相关图，可以发现在间隔为3的地方相关系数在95%的置信区间外，其它都在置信区间内。

另外，还有一个QQ图可以帮助我们来查看残差序列是否接近于白噪声。

QQ图的“Q”代表分位（Quantile）。QQ图示是通过画出分位数来比较两个概率分布的图形方法。点(x,y)对应于第一个分布(x轴)的分位数和第二个分布(y轴)相同的分位数。如果被比较的两个分布比较相似，则其QQ图近似地位于y = x上。

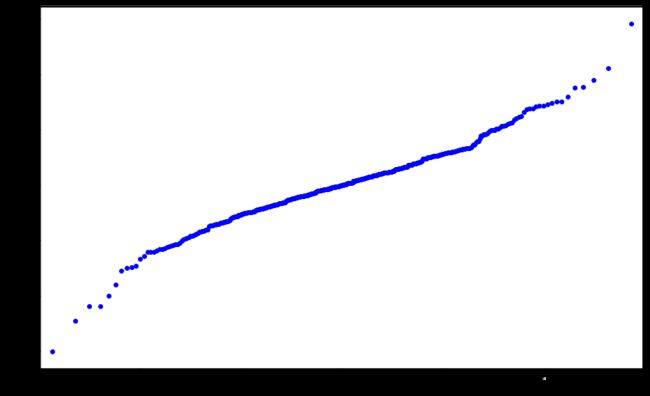
我们画出残差序列的QQ图就是在比较预测序列和原始序列的接近程度。

从QQ图可以整体的分位图与y = x还是有一定偏差的。