【因果推断与机器学习】Causal Inference: Chapter_3
Identification
Introduction
在介绍这节的补充内容呢,我想先引进一个著名的**“辛普森悖论”**。
辛普森医生发现了一种新药,这种新药可以降低心脏病发作的风险,于是他开始查找历史的实验数据。他注意到,如果男性患者服用了这种药,心脏病发作的风险反而高了。然后他再转向女性患者,结果大吃一惊:女性患者复用这种药以后心脏病发作的风险也变高了。但是这种药从数据上来说对整个人群来说是有益的。为什么对女性、男性有害,但是对人类有益?
以数据表明这种现象如下。
| 服药组 | 未服药组 | |
|---|---|---|
| 男性( 357 700 = 0.51 ) \frac {357}{700}=0.51) 700357=0.51)) | 81 87 = 0.93 \frac {81}{87}=0.93 8781=0.93 | 234 270 = 0.87 \frac {234}{270}=0.87 270234=0.87 |
| 女性( 363 700 = 0.49 \frac {363}{700}=0.49 700363=0.49) | 192 263 = 0.73 \frac {192}{263}=0.73 263192=0.73 | 55 80 = 0.69 \frac {55}{80}=0.69 8055=0.69 |
| 总数 | 273 350 = 0.78 \frac {273}{350}=0.78 350273=0.78 | 289 350 = 0.83 \frac {289}{350}=0.83 350289=0.83 |
其中反映了男性和女性服药与不服药的比例是不同的,男性服药的人数远远小于不服药的人数,而女性服药的人数远远大于不服药的人数,因此性别是复用药物和心脏病发作的一个cofunder。辛普森悖论不过是非常简单的数学现象。如果 A / B > a / b A/B \: > \: a/b A/B>a/b and C / D > c / d C/D \: > \:c/d C/D>c/d, 那么从中不能推出 ( A + C ) / ( B + D ) > ( a + b ) / ( c + d ) (A +C)/(B+D) \: > \: (a+b)/(c+d) (A+C)/(B+D)>(a+b)/(c+d)
Identification under Graphical Constraints
使用 d o − c a c u l u s do-caculus do−caculus我们可以在许多情况下推导出简单的因果识别方法。在本 节中介绍两种方法一个是(1)调整公式,(2)前门路径法则 。
Adjustment Formula
举个例子,让我们考虑一个简单的因果概率分布 P ( B ∣ d o ( A ) ) P(B|do(A)) P(B∣do(A))在某个因果图 G G G中。在这里,我们将展示对这一因果目标的两种简单操作如何为我们提供一种有用的识别方法,称为调整公式:
P ( B ∣ d o ( A ) ) = ∑ Z P ( B , Z ∣ d o ( A ) ) = ∑ Z P ( B ∣ d o ( A ) , Z ) P ( Z ∣ d o ( A ) ) = ∑ Z P ( B ∣ d o ( A ) , Z ) P ( Z ) i f ( Z ⊥ a ) G d o ( A ) = ∑ Z P ( B ∣ A , Z ) P ( Z ) i f ( B ⊥ A ∣ Z ) G A \begin{aligned} P(B|do(A))\: &=\: \sum_{Z}P(B,Z|do(A)) \\ &= \sum_{Z}P(B|do(A),Z)P(Z|do(A)) \\ &=\sum_{Z}P(B|do(A),Z)P(Z) \quad if (Z\bot a)G_{do(A)} \\ &=\sum_{Z}P(B|A,Z)P(Z) \quad if \quad(B\bot A|Z)_{GA} \end{aligned} P(B∣do(A))=Z∑P(B,Z∣do(A))=Z∑P(B∣do(A),Z)P(Z∣do(A))=Z∑P(B∣do(A),Z)P(Z)if(Z⊥a)Gdo(A)=Z∑P(B∣A,Z)P(Z)if(B⊥A∣Z)GA
第一步其实反映了就算经过干预变量A,变量Z的边缘分布不变。第二步可以通过全概率公式得到,第三步是使用了 d o − c a c u l u s do-caculus do−caculus的规则-3,也就是变量Z和变量A是相互独立的。第四步应用 d o − c a c u l u s do-caculus do−caculus的规则-2(在变量z,d-分离变量a和变量b)其中变量a的所有出度边都已经被移除。最终得到的这个公式也被称为调整公式 。运算过程也叫作调整 Z Z Z。
注意到对于一个成功的因果标识来说 P ( A ∣ Z ) P(A|Z) P(A∣Z)应该是严格的大于0的。如果在已观测的数据中没有关于变量 A = a A=a A=a的数据,那么就不可能的识别出 P ( B ∣ d o ( A ) ) P(B|do(A)) P(B∣do(A))因为 p ( b ∣ a , z ) ) p(b|a,z)) p(b∣a,z))是不确定的。这一要求通常被称为因果识别的重叠假设,我们将在第4章的评估中进一步讨论其含义。
为了解释以上公式我们以因果图来表示上述关系
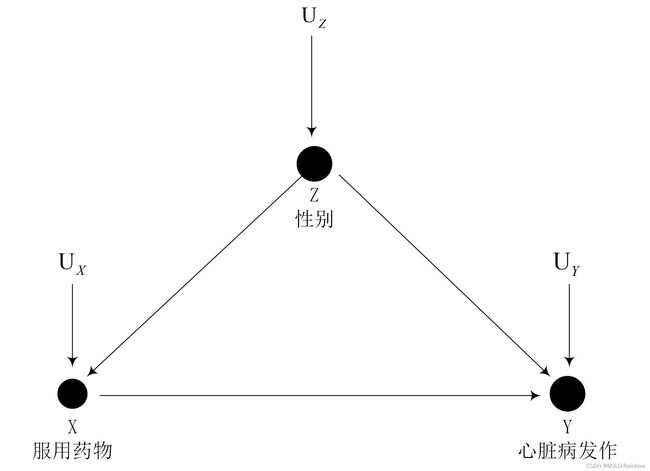
为了找出该药物在人群中到底是有益还是有害,我们利用章节2 中的假设干预的方法计算因果效应:
P ( Y ∣ d o ( x = 1 ) ) − P ( Y = 1 ∣ d o ( x = 0 ) ) P(Y|do(x=1))\: - \: P(Y=1|do(x=0)) P(Y∣do(x=1))−P(Y=1∣do(x=0))
由于假设了治疗变量,所以得到新的因果图如图2所示
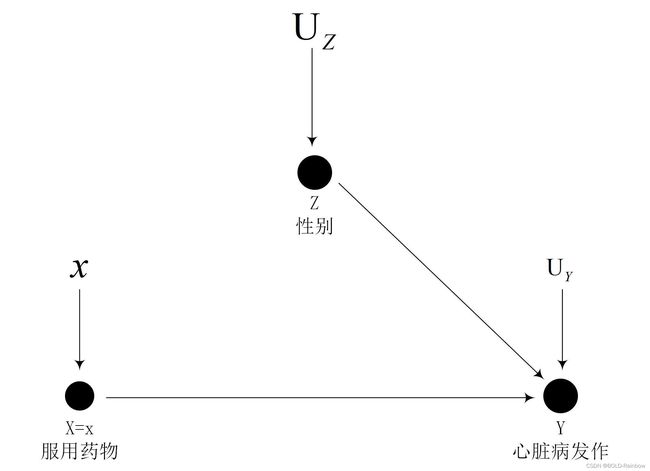
经过修改后的的因果图概率表示为: P ( Y = y ∣ d o ( X = x ) ) P(Y=y|do(X=x)) P(Y=y∣do(X=x))变成 P m ( Y = y ∣ X = x ) P_m{(Y=y|X=x)} Pm(Y=y∣X=x)。其中m下标表示修改后的概率分布。同时我们知道,经过干预后 Z Z Z的边缘分布是不变的,也就是:
P m ( Z = z ) = P ( Z = z ) P_m{(Z=z)}\: =\: P(Z=z) Pm(Z=z)=P(Z=z)
同时,经过干预后,以 Z Z Z和 X X X为条件的 Y Y Y的条件概率是不变的,也就是:
P m ( Y = y ∣ Z = z , X = x ) = P ( Y = y ∣ Z = z , X = x ) P_m{(Y=y|Z=z,X=x)}=P(Y=y|Z=z,X=x) Pm(Y=y∣Z=z,X=x)=P(Y=y∣Z=z,X=x)
将以上式子联系在一起就有:
P ( B ∣ d o ( A ) ) = P m ( Y = y ∣ X = x ) = ∑ Z P m ( Y = y ∣ X = x , Z = z ) P m ( Z = z ∣ X = x ) = ∑ Z P m ( Y = y ∣ X = x , Z = z ) P m ( Z = z ) = ∑ Z P ( Y = y ∣ X = x , Z = z ) P ( Z = z ) \begin{aligned} P(B|do(A))\: &= P_m{(Y=y|X=x)} \\ &= \sum_{Z}P_m{(Y=y|X=x,Z=z)}P_m{(Z=z|X=x)} \\ &=\sum_{Z}P_m{(Y=y|X=x,Z=z)}P_m{(Z=z)} \\ &=\sum_{Z}P{(Y=y|X=x,Z=z)}P(Z=z) \end{aligned} P(B∣do(A))=Pm(Y=y∣X=x)=Z∑Pm(Y=y∣X=x,Z=z)Pm(Z=z∣X=x)=Z∑Pm(Y=y∣X=x,Z=z)Pm(Z=z)=Z∑P(Y=y∣X=x,Z=z)P(Z=z)
因此考虑到性别这个混杂因素计算过程如下:
P ( Y = 1 ∣ d o ( X = 1 ) ) = P ( Y = 1 ∣ X = 1 , Z = 1 ) P ( Z = 1 ) + P ( Y = 1 ∣ X = 1 , Z = 0 ) P ( Z = 0 ) P(Y=1|do(X=1))=P(Y=1|X=1,Z=1)P(Z=1)+P(Y=1|X=1,Z=0)P(Z=0) P(Y=1∣do(X=1))=P(Y=1∣X=1,Z=1)P(Z=1)+P(Y=1∣X=1,Z=0)P(Z=0)
进而得到:
P ( Y = 1 ∣ d o ( X = 1 ) ) = 0.832 P(Y=1|do(X=1))=0.832 P(Y=1∣do(X=1))=0.832
P ( Y = 1 ∣ d o ( X = 0 ) ) = 0.781 P(Y=1|do(X=0))=0.781 P(Y=1∣do(X=0))=0.781
The Front-door Criterion
谈到 F r o n t − d o o r C r i t e r i o n Front-door \: Criterion Front−doorCriterion就不得不提及后门法则。举个例子,以上内容提到的辛普森悖论的例子里含有一个性别的混杂因素,而后门路径法则的作用就是为了消除混杂因素的。在这里我们必须要明白什么是后门路径,什么是前门路径。以图1中变量X和变量Y为例,变量 X 和 Y之间的后门路径就是连接 X 和 Y 但箭头不从变量 X 出发的路径,即路径 X ← Z → Y X\leftarrow Z \rightarrow Y X←Z→Y称为X和Y之间的后门路径。从 X → Y X\rightarrow Y X→Y的路径就是前门路径。
总结一下后门路径法则就是:假如变量Z阻断了所有变量X和变量Y之间的路径,这个路径连接了X且指向变量X,也就是说变量Z中的节点都不是X的后代节点,称变量Z满足(X,Y)的后门路径准则。
根据上一节所写到的内容就可以写出调整公式:
P ( Y ∣ d o ( X = x ) ) = ∑ Z P ( Y = y ∣ X = x , Z = z ) P ( Z = z ) P(Y|do(X=x))=\sum_ZP(Y=y|X=x,Z=z)P(Z=z) P(Y∣do(X=x))=Z∑P(Y=y∣X=x,Z=z)P(Z=z)
进入正题,到底什么是前门路径法则?
调整公式是可以仅从图形假设和do-calculus导出的识别方法之一。有时,有效调整集所需的一个或多个变量未被观察到(比如说辛普森悖论中的性别变量)在这种情况下,我们不能在调整公式中使用该特定的调整集。如果没有有效的调整集,其变量都被观察到,那么我们不能使用调整公式进行识别得到因果公式。
然而,应用do-calculus的规则可以产生其他策略。前门路径法则就是这样一种方法,当应用调整公式所必需的混杂变量未被观察到时,用于识别因果效应。考虑图3,该图示出了未观察到的混杂因素 U 使得无法应用调整公式。在这个简单的示例中,唯一有效的调整集是 U。 因此,没有观察 U,我们无法计算调整公式来识别 P ( C ∣ d o ( A ) ) P(C|do(A)) P(C∣do(A))直接。
考虑图3中的节点B,由于节点A不是直接作用于节点C而是通过节点B,而且并不具有相同的混杂因素。这种特殊的结构将使我们应用前门路径法则,而不能应用调整公式来识别目标因果效应。
前门路径法则的关键是我们可以分解变量A和C之间的因果关系,对于图3来说分解的因果效应式子为:
P ( C ∣ d o ( A ) ) = ∑ B P ( C ∣ d o ( B ) ) P ( B ∣ d o ( A ) ) P(C|do(A))=\sum_B{P(C|do(B))P(B|do(A))} P(C∣do(A))=B∑P(C∣do(B))P(B∣do(A))

现在让我们来看一下这些个公式中的因子,我们在仅使用我们能够观察到的数据的情况下有什么办法来解决识别出 P ( C ∣ d o ( B ) ) P(C|do(B)) P(C∣do(B))和 P ( B ∣ d o ( A ) ) P(B|do(A)) P(B∣do(A)),在这种情况下每个因果公式在使用调整公式和 d o − c a c u l u s do-caculus do−caculus规则2的条件下很容易识别出来。
首先根据调整公式得到 P ( C ∣ d o ( B ) ) = ∑ A P ( C ∣ B , A ) P ( A ) P(C|do(B))=\sum_AP(C|B,A)P(A) P(C∣do(B))=∑AP(C∣B,A)P(A)
根据do运算的规则2可以得到 P ( B ∣ d o ( A ) ) = P ( B ∣ A ) P(B|do(A))=P(B|A) P(B∣do(A))=P(B∣A)
结合在一起就有了:
P ( C ∣ d o ( A ) ) = ∑ B ∑ A P ( C ∣ B , A ) P ( A ) P ( B ∣ A ) P(C|do(A))=\sum_B\sum_AP(C|B,A)P(A)P(B|A) P(C∣do(A))=B∑A∑P(C∣B,A)P(A)P(B∣A)
Parametric Assumptions and Instrumental Variables
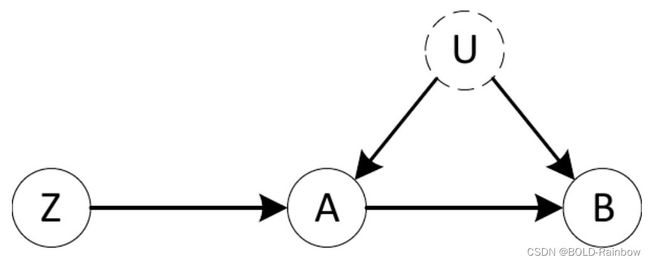
考虑图4所示的因果图。如果我们的目标是确定 P ( B ∣ d o ( A ) ) P(B|do(A)) P(B∣do(A)),我们可以很容易地看出,调整公式不适用,因为混淆特征U未被观察到。由于A和B之间没有中介变量,我们也不能应用前门标准。事实上,A对B的影响仅基于图形假设是无法识别的。
这种因果图很常见。例如,我们经常处于这样的情况:我们有能力进行部分随机化的实验,我们可以随机化Z,但不能直接控制我们主要关注的因子A。例如,这可能发生在对人的实验中,我们可能通过推荐、鼓励或奖励来影响个人的决定,但在其他方面无法完全控制。这也可能发生在许多自然环境中,其中一些可观察到的独立因素,如天气,在确定a中起部分作用。
然而,Z对A的影响有一个有趣的机会。因为在这条路径上Z和B被结点A给d分离了,我们可以很容易的识别出 P r ( A ∣ d o ( Z ) ) = P r ( A ∣ Z ) Pr(A|do(Z))=Pr(A|Z) Pr(A∣do(Z))=Pr(A∣Z),同样的我们可得出 P r ( B ∣ d o ( z ) ) = P r ( B ∣ d o ( z ) ) Pr(B|do(z))=Pr(B|do(z)) Pr(B∣do(z))=Pr(B∣do(z))。
工具变量法是一种利用辅助变量Z来分离因果效应的识别方法。遵循图4的图形结构的变量称为工具变量。工具变量设置满足几个标准2:
- Z和B是独立的,如果不是A。更正式地说,Z和B在图Gnull(A)中是d-分离的。这意味着Z仅通过通过A的路径影响B,并且Z和B由于共同原因而不相关。
- Z影响A。Z和A不是d分离的,P(A|do(Z))是可识别的。
- Z对A和A对B的影响对于未观察变量U是均匀的。
前两个条件可以从因果图中读取,而第三个条件是附加的参数约束。第一个条件确保,无论Z对B有什么影响,它只能流过A。Z对B的直接影响不可能不经过A。此外,Gnull(A)中Z和B的d分离意味着Z独立于路径A→B上的混杂因子U。
第二个条件表明Z对a具有非零影响,并且该影响是可识别的。从直觉上讲,Z对B的影响可以被认为是Z对A的影响和A对B的作用的组合,因此,如果Z对A没有影响,它将不会给我们提供关于A的有用信息。在所示的特定图表中,我们可以看到, P ( A ∣ d o ( Z ) ) = P ( A ∣ Z ) P(A|do(Z))=P(A | Z) P(A∣do(Z))=P(A∣Z)是很容易识别的,因为Z和A没有共同的原因(在我们的示例中,Z是随机的)。
最后一个条件是,假设Z对A的影响是均匀的(即,U不修改Z对A影响),并且A对B的影响也是均匀的(U不修改A对B影响)。这将使我们能够确保我们对Z对A的影响以及Z对B的间接影响的观察不会与未观察到的因素U的任何相互作用纠缠在一起。