G2O库:图优化库基础使用,以曲线拟合(一元边问题)为例
g2o库简介
g2o(General Graphic Optimization, G 2 O G^2O G2O)是基于图优化实现非线性最小二乘问题求解的开源 C++ 框架。
Github主页:https://github.com/RainerKuemmerle/g2o
该库的核心类如下:
图优化理论
关于图论的基础理论可以参考博主另一篇博文:u图论、图搜索算法 中关于图的相关内容进行学习。
应注意,g2o中采用顶点(Vertex)表示节点(Node),两者为同一物体。
若用节点表示优化变量,边表示误差项,则可将一个非线性最小二乘问题描述为一个图结构。此处若采用概率图的定义,则可称其为贝叶斯图或因子图。
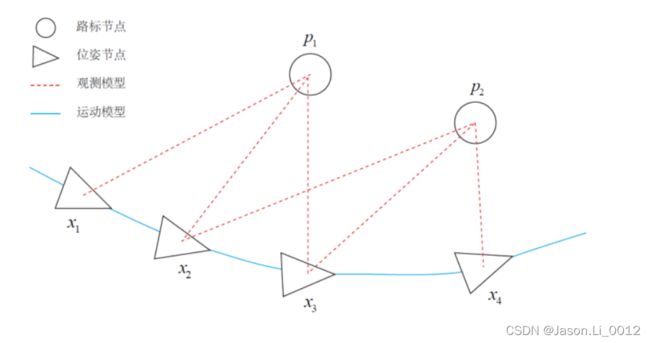
如下图,对相机运动位姿进行构建图结构。图中,采用圆形节点表示路标点;采用三角形节点表示相机位姿;采用实现边表示相机运动模型;采用虚线表示观测模型:
通常可预先进行孤立节点去除 和优先优化边数较多 (也即度数较大 )的节点。
g2o编译安装
首先下载g2o库的源码:
git clone https://github.com/RainerKuemmerle/g2o
其次,安装依赖项,部分依赖项在Ceres库安装时已经完成:
sudo apt install -y qt5-qmake qt5-default libqglviewer-dev-qt5 libsuitesparse-dev libcxsparse3 libcholmod3
随后,进入源码目录进行编译:
# 新建编译目录
cd g2o && mkdir build && cd build
# 编译
cmake ..
make -j12
编译完成后,对生成库文件进行安装:
# 安装
sudo make install
默认安装位置如下:
# include
/usr/local/g2o
# lib
/usr/local/lib/
工程配置
依旧采用CLion+Ubuntu20.04进行开发,新建工程Study。
工程结构
结构如下:
.
├── CMakeLists.txt
├── include
│ └── main.h
└── src
├── CMakeLists.txt
└── main.cpp
子目录include用于存放头文件;子目录src用于存放源码
CMake配置
根目录下CMakeLists.txt文件内容如下:
# cmake version
cmake_minimum_required(VERSION 3.21)
# project name
project(Study)
# cpp version
set(CMAKE_CXX_STANDARD 14)
# eigen
include_directories("/usr/include/eigen3")
# g2o
find_package(g2o REQUIRED)
include_directories(${g2o_INCLUDE_DIRS})
# opencv
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
# incldue
include_directories(include)
# src
add_subdirectory(src)
src目录下CMakeLists.txt文件内容如下:
# exec
add_executable(Study main.cpp)
# link opencv
target_link_libraries(Study ${OpenCV_LIBS})
# link g2o
target_link_libraries(Study g2o_core g2o_stuff)
此处注意,博主target_link_libraries部分若直接链接${g2o_LIBRARIES}时,会报错如下:
undefined reference to g2o::xxxxxxxx
也即,未链接成功库文件,故而直接链接对应库文件。
头文件配置
include目录中头文件main.h内容如下:
#ifndef STUDY_MAIN_H
#define STUDY_MAIN_H
#include 主要导入Eigen库用于矩阵数据表示,Opencv库用于随机数生成,g2o库用于图优化非线性最小二乘求解。
源文件
src下源文件main.cpp初始内容如下:
#include "main.h"
int main()
{
return 0;
}
g2o库API
采用g2o库进行图优化,主要具有如下几步:
- 定义图中节点、边的类型
- 构建图结构
- 选定优化算法
- 优化并得到结果
曲线拟合问题
此处,依旧以手写高斯-牛顿法为例,学习g2o库的使用。关于问题的描述,参见问题描述如下:曲线拟合模型构建
首先将曲线拟合问题构建为一个图,采用节点表示优化变量,采用边表示误差项:
曲线拟合问题中,待优化的变量为曲线模型的参数: a 、 b 、 c a、b、c a、b、c,误差项为一组组包含噪声的数据。
节点类的定义
节点类继承于g2o::BaseVertex
int D:优化变量的维度typename T:优化变量的数据类型
例如构建一个三维Eigen::Vector3d类型的优化变量节点类:
class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {}
此处定义派生类的名字为CurveFittingVertex。
对于节点的定义,还需要重写几个虚函数。
重置函数
类的成员函数setToOriginImpl(),用于对优化变量_estimate的值进行初始化。
如下述重置函数,将三维优化变量初始化为0:
virtual void setToOriginImpl() override
{
_estimate << 0, 0, 0;
}
更新函数
类的成员函数oplusImpl(const double *update)用于定义节点更新的方式,也即用于处理 x k + 1 = x k + Δ x x_{k+1}=x_k+\Delta x xk+1=xk+Δx的过程。
const double *update:指针数据,更新量
应注意,对于表示不同用处的变量,使用不同方式计算增量的更新。例如,曲线拟合问题中只需要使用简单的加法进行更新即可:
virtual void oplusImpl(const double *update) override
{
_estimate += Vector3d(update);
}
而对于如相机位姿问题的更新,则可使用李群的扰动模型进行更新(左乘扰动、右乘扰动)
存盘、读盘函数
类的成员函数read(istream &in)和write(istream &out)用于存盘、读盘。
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
曲线拟合问题的节点定义
对于上述曲线拟合问题,节点的定义如下:
// 节点类,优化变量为3维,Eigen::Vector3d类型的数据
class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {
public:
// 对齐
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 重置函数
virtual void setToOriginImpl() override {
_estimate << 0, 0, 0;
}
// 更新函数
virtual void oplusImpl(const double *update) override {
_estimate += Vector3d(update);
}
// 读盘函数、存盘函数:留空,暂时不用
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
成员变量EIGEN_MAKE_ALIGNED_OPERATOR_NEW声明在new一个这样类型的对象时,解决对齐问题。
边类的定义
边类根据边链接的节点为一个或是两个而继承不同的类。
一元边问题继承于类g2o::BaseUnaryEdge
int D:误差项的维度typename E:误差项的数据类型typename VertexXi:边链接的节点类型
二元边问题继承于类g2o::BaseBinaryEdge
int D:误差项的维度typename E:误差项的数据类型typename VertexXi:边链接的第一个节点的类型typename VertexXj:边链接的第二个节点的类型
例如,对于曲线拟合问题,应构建一个一维double类型的一元类,链接的节点类型为CurveFittingVertex:
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {}
此处定义派生类的名字为CurveFittingEdge。
同样,对于边的定义,也需要重写几个虚函数。
构造函数
边类在被实例化时,需要传入对应的特征 x x x,使用类的私有成员_x接受:
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
在g2o中,使用私有成员_measurement存储观测数据 y y y
误差计算函数
类的成员函数computeError()用于定义边的误差计算函数,误差函数主要用于获取链接节点的值并计算相应的残差值。
例如,曲线拟合的误差函数如下:
virtual void computeError() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 计算误差值
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
在曲线拟合问题中,优化变量为一个三维向量,对应曲线参数:a、b、c,对应的误差计算公式如下:
e r r o r = y − e x p ( a x 2 + b x + c ) error = y-exp(ax^2+bx+c) error=y−exp(ax2+bx+c)
其中,y为观测数据,计算得到的误差值error用于计算导数。
雅克比计算函数
类的成员函数linearizeOplus()用于定义边的雅克比计算函数。同样,雅克比计算函数获取边链接的节点及其对应的优化变量的值,从而求解雅克比矩阵的值。
如曲线拟合问题的雅克比计算函数如下:
virtual void linearizeOplus() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 雅克比矩阵求解
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
此处注意,对于一元边问题,只需要计算_jacobianOplusXi即可;
对于二元边问题 ,应同时计算_jacobianOplusXi和_jacobianOplusXj的值。
存盘、读盘函数
类的成员函数read(istream &in)和write(istream &out)用于存盘、读盘。
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
曲线拟合问题的边定义
对于上述曲线拟合问题,边的定义如下:
// 边类, 误差项为1维double类型的数据,边链接的节点类型为CurveFittingVertex类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
// 对齐
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 构造函数
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 边的误差计算函数
virtual void computeError() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 计算残差值
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 边的雅克比计算函数
virtual void linearizeOplus() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 求导
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
// 读盘函数、存盘函数:留空,暂时不用
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
private:
double _x; // x 值, y 值为 _measurement
};
成员变量EIGEN_MAKE_ALIGNED_OPERATOR_NEW声明在new一个这样类型的对象时,解决对齐问题。
曲线拟合数据生成
完成对节点和边类型的构建后,首先应在main函数中生成使用的数据:
int main()
{
/*-------- 初始参数配置 --------*/
// 实际曲线参数
double ar = 1.0, br = 1.0, cr = 1.0;
// 估计曲线参数初始值
double ae = 2.0, be = 1.0, ce = 5.0;
// 采样观测数据点个数
int N = 100;
// 噪声标准差及其倒数
double w_sigma = 1.0;
// 随机数生成器
cv::RNG rng;
/*-------- 观测数据生成 --------*/
vector<double> x_data, y_data;
for(int i = 0; i < N; i++){
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x +br * x + cr) + rng.gaussian(w_sigma * w_sigma));
}
return 0;
}
构建优化器
完成初始数据的生成后,在主函数中即可构建图模型的配置。
线性求解器、误差块
首先,定义问题中线性求解器、误差块的类型。此处曲线拟合问题的优化变量为三维,误差项为一维:
// 误差项的类型:误差项的优化变量维度为3、误差项的值维度为1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
// 求解器的类型:使用LinearSolverDense求解
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
线性求解器的类型可选LinearSolverDense、LinearSolverPCG、LinearSolverCSparse、LinearSolverCholmod
梯度下降方法
随后,设置梯度下降的方式:
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
此处选择GN法,可选GN法、LM法、DogLeg法,分别对应的API如下:
-
GN法
g2o::OptimizationAlgorithmGaussNewton(std::unique_ptr<Solver> solver); -
LM法
g2o::OptimizationAlgorithmLevenberg(std::unique_ptr<Solver> solver); -
DogLeg法
g2o::OptimizationAlgorithmDogleg(std::unique_ptr<BlockSolverBase> solver);
曲线拟合问题优化器
曲线拟合问题的优化器构建如下:
// 误差项的类型:误差项的优化变量维度为3、误差项的值维度为1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
// 线性求解器的类型:使用LinearSolverDense求解
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
// 优化器:设置采用GN法进行求解
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
图模型建立
设置优化器
首先构建一个图模型并设置优化器
// 图模型
g2o::SparseOptimizer optimizer;
// 设置优化器
optimizer.setAlgorithm(solver);
// 打开调试输出
optimizer.setVerbose(true);
添加节点
向构建的图模型中添加节点:
// 实例化节点类型
CurveFittingVertex *v = new CurveFittingVertex();
// 优化变量初始化
v->setEstimate(Eigen::Vector3d(ae, be, ce));
// 设置图中节点id
v->setId(0);
// 将节点加入图模型
optimizer.addVertex(v);
添加边
使用遍历方式将生成的数据点逐一填入边中:
for (int i = 0; i < N; i++)
{
// 实例化边类型,传入特征x
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
// 设置图中边id
edge->setId(i);
// 设置连接的节点:节点编号和节点对象
edge->setVertex(0, v);
// 设置观测数据
edge->setMeasurement(y_data[i]);
// 设置信息矩阵:协方差矩阵之逆
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
// 将边加入图模型
optimizer.addEdge(edge);
}
开始优化
最后,开始进行优化问题的求解:
/*-------- 图优化开始 --------*/
cout << "start optimization" << endl;
// 初始化优化
optimizer.initializeOptimization();
// 优化次数设置
optimizer.optimize(10);
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
实例:曲线拟合
代码
完整代码如下:
#include "main.h"
// 节点类,优化变量为3维,Eigen::Vector3d类型的数据
class CurveFittingVertex : public g2o::BaseVertex<3, Vector3d> {
public:
// 对齐
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 重置函数
virtual void setToOriginImpl() override {
_estimate << 0, 0, 0;
}
// 更新函数
virtual void oplusImpl(const double *update) override {
_estimate += Vector3d(update);
}
// 读盘函数、存盘函数:留空,暂时不用
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
// 边类, 误差项为1维double类型的数据,边链接的节点类型为CurveFittingVertex类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
// 对齐
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 构造函数
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 边的误差计算函数
virtual void computeError() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 计算残差值
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 边的雅克比计算函数
virtual void linearizeOplus() override {
// 获取节点
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
// 获取节点的优化变量(节点值)
const Eigen::Vector3d abc = v->estimate();
// 求导
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
// 读盘函数、存盘函数:留空,暂时不用
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
private:
double _x; // x 值, y 值为 _measurement
};
int main()
{
/*-------- 初始参数配置 --------*/
// 实际曲线参数
double ar = 1.0, br = 1.0, cr = 1.0;
// 估计曲线参数初始值
double ae = 2.0, be = 1.0, ce = 5.0;
// 采样观测数据点个数
int N = 100;
// 噪声标准差及其倒数
double w_sigma = 1.0;
// 随机数生成器
cv::RNG rng;
/*-------- 观测数据生成 --------*/
vector<double> x_data, y_data;
for(int i = 0; i < N; i++){
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x +br * x + cr) + rng.gaussian(w_sigma * w_sigma));
}
/*-------- 优化器配置 --------*/
// 误差项的类型:误差项的优化变量维度为3、误差项的值维度为1
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
// 线性求解器的类型:使用LinearSolverDense求解
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
// 优化器:设置采用GN法进行求解
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
/*-------- 图模型配置 --------*/
// 图模型
g2o::SparseOptimizer optimizer;
// 设置优化器
optimizer.setAlgorithm(solver);
// 打开调试输出
optimizer.setVerbose(true);
// 实例化节点类型
CurveFittingVertex *v = new CurveFittingVertex();
// 优化变量初始化
v->setEstimate(Eigen::Vector3d(ae, be, ce));
// 设置图中节点id
v->setId(0);
// 将节点加入图模型
optimizer.addVertex(v);
// 向图模型加入边
for (int i = 0; i < N; i++)
{
// 实例化边类型,传入特征x
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
// 设置图中边id
edge->setId(i);
// 设置连接的节点:节点编号和节点对象
edge->setVertex(0, v);
// 设置观测数据
edge->setMeasurement(y_data[i]);
// 设置信息矩阵:协方差矩阵之逆
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
// 将边加入图模型
optimizer.addEdge(edge);
}
/*-------- 图优化开始 --------*/
cout << "start optimization" << endl;
// 求解开始计时t1
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
// 初始化优化
optimizer.initializeOptimization();
// 优化次数设置
optimizer.optimize(10);
// 求解结束计时t2
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
// 求解总用时
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
cout << "estimated model: " << abc_estimate.transpose() << endl;
return 0;
}
输出
输出结果如下:
start optimization
solve time cost = 0.00741664 seconds.
estimated model: 0.877649 1.21235 0.931272
iteration= 0 chi2= 12378200.264531 time= 0.000666326 cumTime= 0.000666326 edges= 100 schur= 0
iteration= 1 chi2= 1618271.477542 time= 0.000780621 cumTime= 0.00144695 edges= 100 schur= 0
iteration= 2 chi2= 199423.333138 time= 0.000621562 cumTime= 0.00206851 edges= 100 schur= 0
iteration= 3 chi2= 20992.691489 time= 0.000643664 cumTime= 0.00271217 edges= 100 schur= 0
iteration= 4 chi2= 1519.455061 time= 0.000571236 cumTime= 0.00328341 edges= 100 schur= 0
iteration= 5 chi2= 132.709242 time= 0.000571791 cumTime= 0.0038552 edges= 100 schur= 0
iteration= 6 chi2= 102.041451 time= 0.000593103 cumTime= 0.0044483 edges= 100 schur= 0
iteration= 7 chi2= 102.004182 time= 0.000571012 cumTime= 0.00501932 edges= 100 schur= 0
iteration= 8 chi2= 102.004182 time= 0.000571102 cumTime= 0.00559042 edges= 100 schur= 0
iteration= 9 chi2= 102.004182 time= 0.000571705 cumTime= 0.00616212 edges= 100 schur= 0