R语言学习笔记9_多元统计分析介绍
目录
- 九、多元统计分析介绍
-
- 9.1 主成分分析与因子分析
-
- 9.1.1 主成分的R通用程序
- 9.1.2 因子分析R通用程序
- 9.2 判别分析
-
- 9.2.1 距离判别
- 9.2.2 Fisher判别法
- 9.2.3 R通用程序
- 9.3 聚类分析
-
- 9.3.1 基本思想
- 9.3.2 R通用程序
- 9.4 典型相关分析
-
- 9.4.1 基本思想
- 9.4.2 R通用程序
- 9.5 对应分析
-
- 9.5.1 R通用程序
九、多元统计分析介绍
研究客观事物中1)多变量(多因素或多指标)之间的相互关系2)多样品对象之间差异3)以多个变量为代表的多元随机变量之间的依赖和差异的现代统计分析理论和方法。
- 主成分分析与因子分析的目的是寻找多个变量的“代表”
- 判别分析能将对象分类到已知类别中
- 聚类分析按照一定的尺度把对象分类
- 典型相关分析研究两组变量之间的相关问题
- 对应分析探究行列变量的关系
9.1 主成分分析与因子分析
9.1.1 主成分的R通用程序
主成分分析:是把多维空间的相关多变量的数据集,通过降维化简为少量且相互独立新综合指标(尽可能多的包括或尽可能不损失原指标群中的主要信息)
princomp(formula, data = NULL, subset, na.action, ...)
princomp(x, cor = FALSE, scores = TRUE, covmat = NULL,
subset = rep_len(TRUE, nrow(as.matrix(x))), fix_sign = TRUE, ...)
formula是没有响应变量的公式;x是用于主成分分析的数据;cor是逻辑变量,cor = FALSE表示用样本的协方差矩阵S作主成分,cor=TRUE表示用样本点相关阵R作主成分分析。
例:学生身体4项指标的主成分分析:随机抽取30名某年级中学生,测量其身高X1,体重X2,胸围X3,坐高X4,数据如下表。试对这30名学生身体的四项指标作主成分分析。
X1 X2 X3 X4 148 41 72 78 139 34 71 76 160 49 77 86 149 36 67 79 159 45 80 86 142 31 66 76 153 43 76 83 150 43 77 79 151 42 77 80 139 31 68 74 140 29 64 74 161 47 78 84 158 49 78 83 140 33 67 77 137 31 66 73 152 35 73 79 149 47 82 79 145 35 70 77 160 47 74 87 156 44 78 85 151 42 73 82 147 38 73 78 157 39 68 80 147 30 65 75 157 48 80 88 151 36 74 80 144 36 68 76 141 30 67 76 139 32 68 73 148 38 70 78
> student<-data.frame(x1<-c(148,139,160,149,159,142,153,150,151,139,140,161,158,140,137,152,149,145,160,156,151,147,157,147,157,151,144,141,139,148),x2<-c(41,34,49,36,45,31,43,43,42,31,29,47,49,33,31,35,47,35,47,44,42,38,39,30,48,36,36,30,32,38),x3<-c(72,71,77,67,80,66,76,77,77,68,64,78,78,67,66,73,82,70,74,78,73,73,68,65,80,74,68,67,68,70),x4<-c(78,76,86,79,86,76,83,79,80,74,74,84,83,77,73,79,79,77,87,85,82,78,80,75,88,80,76,76,73,78))
> student.pr<-princomp(student,cor = T)
> summary(student.pr,loadings=T)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.8817805 0.55980636 0.28179594 0.25711844
Proportion of Variance 0.8852745 0.07834579 0.01985224 0.01652747
Cumulative Proportion 0.8852745 0.96362029 0.98347253 1.00000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
x1....c.148..139..160..149..159..142..153..150..151..139..140.. 0.497 0.543 0.450 0.506
x2....c.41..34..49..36..45..31..43..43..42..31..29..47..49..33.. 0.515 -0.210 0.462 -0.691
x3....c.72..71..77..67..80..66..76..77..77..68..64..78..78..67.. 0.481 -0.725 -0.175 0.461
x4....c.78..76..86..79..86..76..83..79..80..74..74..84..83..77.. 0.507 0.368 -0.744 -0.232
Standard deviation 表示主成分的标准差
Proportion of Variance 表示方差的贡献率
Cumulative Proportion 表示方差的累计贡献率
loadings=T表示列出主成分对应原始变量的系数,因此得到前两个主成分是:
Y1=0.497X1+ 0.543X2+ 0.450x3+ 0.506X4
Y2=0.515X1 - 0.210X2+ 0.462X3 - 0.691X4
由于前两个主成分的累计贡献率已经达到了96.36%,所以取前两个主成分来降维。
9.1.2 因子分析R通用程序
研究相关矩阵的内在依赖关系,把多个显在的变量综合为少数几个不可观测的潜在因子或公共因子。
根据研究对象和分析方法不同,可分为R型和Q型两种:R型因子分析研究指标(变量) 之间的相互关系,通过多变量相关系数矩阵内部结构的研究找出控制所有变量的几个主因子(成分),需要考虑变量量纲及数量级;Q型因子分析研究样品之间控制所有样品的几个主要因素。
factanal(x, factors, data = NULL, covmat = NULL, n.obs = NA,
subset, na.action, start = NULL,
scores = c("none", "regression", "Bartlett"),
rotation = "varimax", control = NULL, ...)
x是用于因子分析的数据;factors表示因子个数,scores表示选用因子得分方法,rotation=“varimax”表示用最大方差旋转。
9.2 判别分析
目的在于对已知归类的数据建立由数值指标构成的归类规则,然后把这样的规则应用到未知归类的样品去归类。
9.2.1 距离判别
计算样品到各类的马氏距离。样品和哪个总体距离最近,就判它属于哪个总体。
9.2.2 Fisher判别法
投影。将K组m维数据投影到某个方向,使投影后组与组之间尽可能地分开。用一元方差分析思想衡量组于组之间是否分开。
9.2.3 R通用程序
lda(formula, data, ..., subset, na.action)
formula用法为groups~x1+x2+…, groups表明总体来源,x1+x2+…表示分类指标;subset指明训练样本
例1:利用R内置数据包鸢尾花Iris进行判别分析
> data("iris")
> attach(iris)
> names(iris)
[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"
> library(MASS)
> iris.lda<-lda(Species~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width)
> iris.lda
Call:
lda(Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width)
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa 5.006 3.428 1.462 0.246
versicolor 5.936 2.770 4.260 1.326
virginica 6.588 2.974 5.552 2.026
Coefficients of linear discriminants:
LD1 LD2
Sepal.Length 0.8293776 0.02410215
Sepal.Width 1.5344731 2.16452123
Petal.Length -2.2012117 -0.93192121
Petal.Width -2.8104603 2.83918785
Proportion of trace:
LD1 LD2
0.9912 0.0088
> iris.pred=predict(iris.lda)$class
> table(iris.pred,Species)
Species
iris.pred setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 1
virginica 0 2 49
> detach(iris)
Group means 包含了每组的平均向量
Coefficients of linear discriminants 线性判别系数
Proportion of trace 表明了第 i 判别式对区分各组贡献的大小
Species 表示将原始数据带入线性判别函数的判别结果,setosa组没有判错, versicolor组有两个判错,virginica组有一个判错。
9.3 聚类分析
事先对总体到底有几种类型无从知晓。
9.3.1 基本思想
先将n个样品各自看成一类,然后规定类与类之间的距离(有多种定义方法)选择距离最小的一对合并成新的一类,计算新类与其他类的距离,再将距离最近的两类合并,每次减少一类,直至所有的样品成为一类为止。
dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p = 2)
method表示计算距离的方法,默认为欧氏距离;diag=T时输出距离矩阵对角线上的距离;upper=T时输出距离矩阵上三角部分。
类与类之间的距离有许多定义方法,主要有以下7种:
- 类平均法(average Linkage)
- 重心法(centroid method)
- 中间距离法(median method)
- 最长距离法(complete method)
- 最短距离法(single method)
- 离差平方和法(ward method)
- 密度估计法(density method)
9.3.2 R通用程序
hclust(d, method = "complete", members = NULL)
d是由dist构成的距离结构,method是系统聚类的方法。
例1:设有5个产品,每个产品测得一项质量指标x,值为:1,2,4.5,6,8,试用最短距离法、最长距离法、中间距离法、离差平方和法分别对5个产品按质量指标进行分类。
> x<-c(1,2,4.5,6,8)
> dim(x)<-c(5,1)
> d<-dist(x)
> hc1<-hclust(d,"single")
> hc2<-hclust(d,"complete")
> hc3<-hclust(d,"median")
> hc4<-hclust(d,"ward")
The "ward" method has been renamed to "ward.D"; note new "ward.D2"
> par(mfrow=c(2,2))
> plot(hc1,hang = -1)
> plot(hc2,hang = -1)
> plot(hc3,hang = -1)
> plot(hc4,hang = -1)
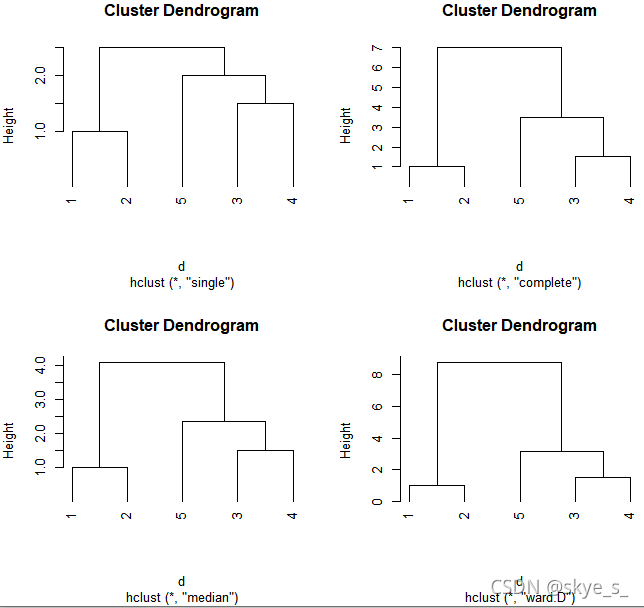
可见,四种分类方法结果一致,都将1,2分在一类,其余在第二类。
例2:对Iris数据集进行聚类分析。假设我们只知道数据内有三种品种的鸢尾花,而不知道每朵花的真正分类,只能凭借花萼及花瓣的长度和宽度去分成三类。
> data("iris")
> attach(iris)
> iris.hc<-hclust(dist(iris[,1:4]))
> plot(iris.hc,hang = -1) #绘制聚类的谱系图
> re<-rect.hclust(iris.hc,k=3) #给定类的个数
> iris.id<-cutree(iris.hc,3) #将数据的分类结果编为三组,分别以1,2,3表示
> table(iris.id,Species)
Species
iris.id setosa versicolor virginica
1 50 0 0
2 0 23 49
3 0 27 1
> detach(iris)
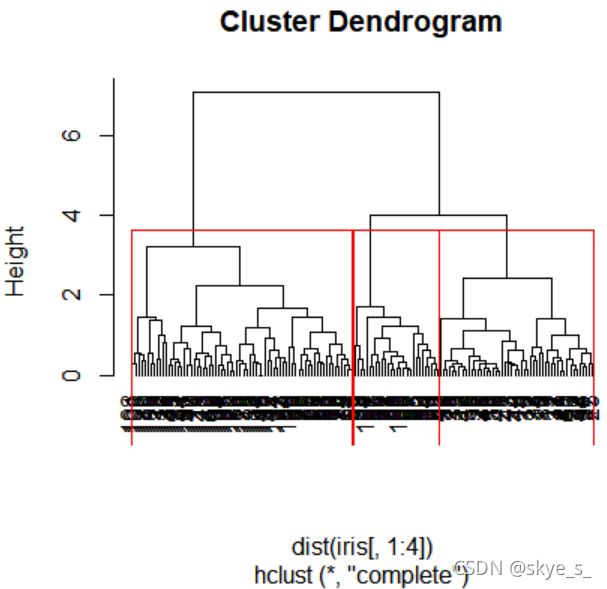
将iris.id与Species作比较发现1应该是setosa类,2应该是virginica类,3是versicolor类。
9.4 典型相关分析
研究两组变量相关关系的一种多元统计方法。(猪肉、牛肉、玉米的价格和其相应销售量的相关关系)
9.4.1 基本思想
首先在每组变量中找出变量的线性组合,使其具有最大相关性;再在每组变量中找出第二对线性组合,使其分别与第一对线性组合不相关,而第二对本身具有最大的相关性,直到两组变量之间的相关性被提取完毕为止。
典型相关关系是对两组变量的每一组作为整体考虑的,因此可以广泛应用于变量群之间的相关分析研究
9.4.2 R通用程序
cancor(x, y, xcenter = TRUE, ycenter = TRUE)
x,y是两组变量的数据矩阵,xcenter和ycenter=T时表示将数据中心化。
9.5 对应分析
研究样本与指标之间的关系。
9.5.1 R通用程序
corresp(x, nf = 1, ...)
x是数据矩阵,nf表示计算因子个数。
例:利用90年代初期对某市若干个郊区已婚妇女的调查资料,主要调查她们对“应该男人在外工作,妇女在家操持家务”的态度,依据文化程度和就业观点两个变量进行分类汇总。
文化程度 就业 观点 非常同意 同意 不同意 非常不同意 小学以下 2 17 17 5 小学 6 65 79 6 初中 41 220 327 48 高中 72 224 503 47 大学 24 61 300 41
> x.df=data.frame(HighlyFor=c(2,6,41,72,24),For=c(17,65,220,224,61),Against=c(17,79,327,503,300),HighlyAgainst=c(5,6,48,47,41))
> rownames(x.df)<-c("BelowPrimary","Primary","Secondary","HighSchool","College")
> library(MASS)
> biplot(corresp(x.df,nf=2))

看就业观点和文化程度的横坐标距离,可以看出对该观点持赞同态度的是小学以下、小学和初中,大学文化程度的妇女主要持不同意或非常不同意的观点,高中文化程度的持有非常不赞同、非常同意两种观点。