非线性优化求解器IPOPT

目录

1、IPOPT的安装（简洁版本）

2、IPOPT测试案例

3、ADOL-C的使用

4、CppAD的使用

 5、IPOPT的initial gauss 以及 warm star

参考链接：

---

优化，在Apollo规划模块中占据了重要的地位

Apollo中 OSQP 和 IPOPT 的应用：

OSQP	IPOPT
参考线：discrete_points_smoother（ FemPosSmooth） 参考线：qp_spline_smoother	参考线：spiral_smoother 分段五次螺旋线非线性优化拟合 参考线：discrete_points_smoother（CosThetaSmooth） ipopt+adol-c
Lattice中横向规划中使用的基于二次规划的轨迹规划	Hybrid A*的轨迹优化
路径规划的QP 速度规划中DP之后的QP	速度规划中DP之后的IPOPT

其中OSQP在之前的文章中测试过，这篇文章主要进行IPOPT的相关实践

非线性优化的一般形式为：

IPOPT是一种常用的非线性优化求解器，使用内点法进行求解

对于复杂问题，需要借助自动微分工具，帮助求解梯度、Yacobian矩阵、Hessian矩阵，

如ADOL-C，CppAD

1、IPOPT的安装（简洁版本）

(1).安装apt包

sudo apt-get install gcc g++ gfortran git patch wget pkg-config liblapack-dev libmetis-dev

(2).安装BLAS and LAPACK

即为前面apt安装的liblapack-dev

(3).安装HSL 官网注册申请下载

需要教育网邮箱申请，

同时下载如下库.并将前面下载的HSL包解压后改名为coinhsl(例如coinhsl-archive-2021.05.05 => coinhsl)后复制到ThirdParty-HSL文件夹中,最后进行编译安装.

git clone https://github.com/coin-or-tools/ThirdParty-HSL.git
cd ThirdParty-HSL
./configure
make
sudo make install
sudo ldconfig

(4).安装IPOPT

Ipopt源码下载

mkdir build
cd build
sudo ../configure --prefix=/usr/local/ #安装到指定位置
sudo make
sudo make test
sudo make install

make test的输出应该如下：

Running unitTests...

Testing AMPL Solver Executable...
    Test passed!
Testing C++ Example...
    Test passed!
Testing C Example...
    Test passed!
Testing Fortran Example...
    Test passed!
Skip testing Java Example (Java interface not build)
Testing sIpopt Example parametric_cpp...
    Test passed!
Testing sIpopt Example redhess_cpp...
    Test passed!
Testing EmptyNLP Example...
    Test passed!
Testing GetCurr Example...
    Test passed!

(5).安装成功与否
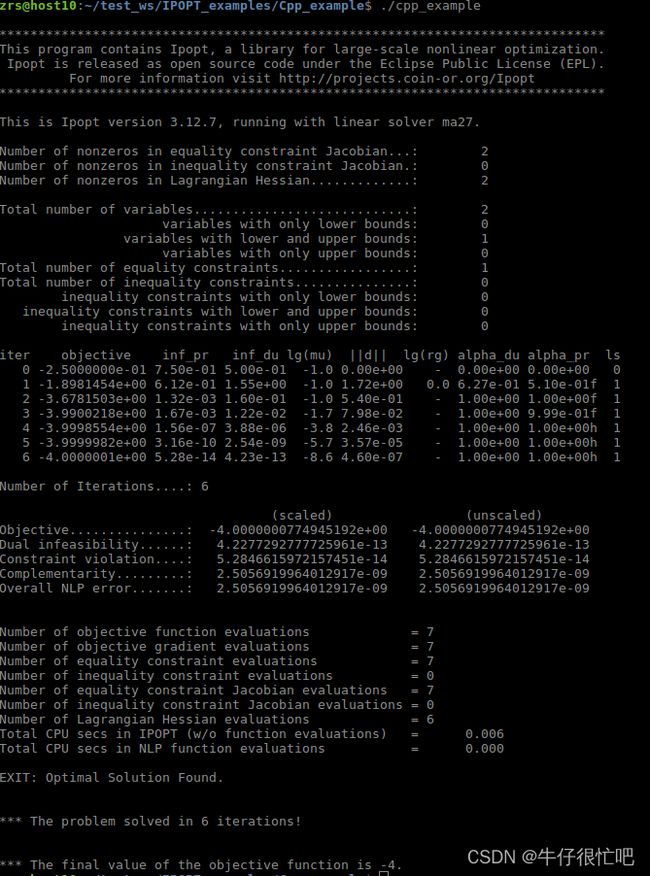
进入IPOPT源码文件夹如下位置,用官方例子测试

cd Ipopt-releases-3.14.2/build/examples/Cpp_example
sudo make
./solver

Ubuntu 16.04 安装Ipopt 3.12.7 和 CppAD - 简书

Ubuntu18.04配置Ipopt，CppAD 通过C++求解最优控制_小朱 智能驾驶的博客-CSDN博客_c++ ipopt

2、IPOPT测试案例

#include "IpIpoptApplication.hpp"
#include "IpSolveStatistics.hpp"
#include "MyNLP.hpp"

#include 

using namespace Ipopt;

int main(int argv, char* argc[])
{
  // Create an instance of your nlp...
  SmartPtr mynlp = new MyNLP();

  // Create an instance of the IpoptApplication
  //
  // We are using the factory, since this allows us to compile this
  // example with an Ipopt Windows DLL
  SmartPtr app = IpoptApplicationFactory();

  // Initialize the IpoptApplication and process the options
  ApplicationReturnStatus status;
  status = app->Initialize();
  if (status != Solve_Succeeded) {
    std::cout << std::endl << std::endl << "*** Error during initialization!" << std::endl;
    return (int) status;
  }

  status = app->OptimizeTNLP(mynlp);

  if (status == Solve_Succeeded) {
    // Retrieve some statistics about the solve
    Index iter_count = app->Statistics()->IterationCount();
    std::cout << std::endl << std::endl << "*** The problem solved in " << iter_count << " iterations!" << std::endl;

    Number final_obj = app->Statistics()->FinalObjective();
    std::cout << std::endl << std::endl << "*** The final value of the objective function is " << final_obj << '.' << std::endl;
  }

  return (int) status;
}

 

3、ADOL-C的使用

待补充

4、CppAD的使用

#include 
#include 

using namespace std;

namespace {
using CppAD::AD;
class FG_eval {
  public:
      typedef CPPAD_TESTVECTOR(AD) ADvector;
      // 
      void operator()(ADvector& fg, const ADvector& x)
      {
          assert(fg.size() == 3);
          assert(x.size() == 4);
          // variables 优化变量
          AD x1 = x[0];
          AD x2 = x[1];
          AD x3 = x[2];
          AD x4 = x[3];
          // f(x) objective function 目标函数
          fg[0] = x1 * x4 * (x1 + x2 + x3) + x3;
          // constraints 约束条件
          fg[1] = x1 * x2 * x3 * x4;
          fg[2] = x1 * x1 + x2 * x2 + x3 * x3 + x4 * x4;
          return;
      }
  };
} //end namespace


bool get_started(void)
{
    bool ok = true;
    size_t i;
    typedef CPPAD_TESTVECTOR(double) Dvector;

    size_t nx = 4; // number of varibles 
    size_t ng = 2; // number of constraints 
    Dvector x0(nx); // initial condition of varibles 初始？

    x0[0] = 1.0;
    x0[1] = 5.0;
    x0[2] = 5.0;
    x0[3] = 1.0;

    // lower and upper bounds for varibles
    Dvector xl(nx), xu(nx);
    for(i = 0; i < nx; i++)
    {
        xl[i] = 1.0;
        xu[i] = 5.0;
    }
	
    //不等式上下界
    Dvector gl(ng), gu(ng);
    gl[0] = 25.0;    gu[0] = 1.0e19;
    gl[1] = 40.0;    gu[1] = 40.0;
    // object that computes objective and constraints
    FG_eval fg_eval;

    // options
    string options;
    // turn off any printing
    options += "Integer print_level  0\n";
    options += "String sb            yes\n";
    // maximum iterations
    options += "Integer max_iter     10\n";
    //approximate accuracy in first order necessary conditions;
    // see Mathematical Programming, Volume 106, Number 1,
    // Pages 25-57, Equation (6)
    options += "Numeric tol          1e-6\n";
    //derivative tesing
    options += "String derivative_test   second-order\n";
    // maximum amount of random pertubation; e.g.,
    // when evaluation finite diff
    options += "Numeric point_perturbation_radius   0.\n";

    //定义solution并求解
    CppAD::ipopt::solve_result solution; // solution
    CppAD::ipopt::solve(options, x0, xl, xu, gl, gu, fg_eval, solution); // solve the problem

    cout << "solution: " << solution.x << endl;

    //check some of the solution values 这个check有什么用？
    ok &= solution.status == CppAD::ipopt::solve_result::success;

    double check_x[]  = {1.000000, 4.743000, 3.82115, 1.379408};
    double check_zl[] = {1.087871, 0.,       0.,       0.      };
    double check_zu[] = {0.,       0.,       0.,       0.      };
    double rel_tol    = 1e-6; // relative tolerance
    double abs_tol    = 1e-6; // absolute tolerance
    for(i = 0; i < nx; i++)
    {
        ok &= CppAD::NearEqual(check_x[i], solution.x[i], rel_tol, abs_tol);
        ok &= CppAD::NearEqual(check_zl[i], solution.zl[i], rel_tol, abs_tol);
        ok &= CppAD::NearEqual(check_zu[i], solution.zu[i], rel_tol, abs_tol);
    }

    return ok;
}

int main()
{
    cout << "CppAD : Hello World Demo!" << endl;
    bool res = get_started();
    cout << "CppAD res:" << res << endl;
    return 0;
}

CMakeList.txt

project(ipopt_test)

cmake_minimum_required (VERSION 3.5)

add_definitions(-std=c++11 -O3)

add_executable(ipopt_test main.cpp)

target_link_libraries(ipopt_test ipopt)

 

 5、IPOPT的initial gauss 以及 warm star

参考链接：

Ipopt: Documentation

非线性优化求解器IPOPT的使用学习 - Challenging-eXtraordinary

基础理论：

导数、梯度、 Jacobian、Hessian - 知乎

Chapter 11 导数、梯度、 Jacobian、Hessian {Gradient Related Concepts} | 数值分析笔记

梯度向量、Jacobian、Hessian矩阵_Alinooo的博客-CSDN博客_梯度向量怎么求

自动微分工具：ADOL-C、CppAD

自动微分的理论：

自动微分 - 知乎

ipopt CppAD 非线性规划_梦醒时分1218的博客-CSDN博客_cppad

无人车系统（十）：c++与python非线性规(优)划（化）工具_昔风不起，唯有努力生存！-CSDN博客 C++自动微分（Automatic differentiation）原理1_Daniel 的技术笔记 不积跬步无以至千里，不积小流无以成江海。-CSDN博客_c++ 自动微分

 自动微分的使用 - propagator的个人空间 - OSCHINA - 中文开源技术交流社区

后记：关于非线性优化，，我只在CasADi（MATLAB，Python）中进行过简单的测试

SX、MX以及Opti方法（像在写数学表达式），使用最基本的Opti方法

还有一种方式是AMPL，我在讲座中看到过

以上方案可以作为研究中初步的仿真测试，实际运行还是要用C++

https://www.youtube.com/watch?v=lx8RcYcYVuU

Convex Optimization | edX

CasADi/ACADOS学习 - 知乎

https://blog.csdn.net/u010442396/category_10110539.html