计算智能课程设计(以人事招聘为例的误差反向传播算法)
写在前面
昨天写了基于感知机的鸢尾花分类,今天下午要考《大数据技术原理》,本来是整个白天的课程设计,因为考试少了一下午。之前看书复习了一波,但记忆是需要反复锤炼的,所以要抓紧写完这个传播算法,抽出时间再去复习会。2021.11.30/2021.12.1/2021.12.2
以人事招聘为例的误差反向传播算法
实验目的
理解多层神经网络的结构和原理,掌握反向传播算法对神经元的训练过程,了解反向传播公式。通过构建 BP 网络实例,熟悉前馈网络的原理及结构。
示例代码
import numpy as np
import matplotlib.pyplot as plt
# 输入数据1行2列,这里只有张三的数据
X = np.array([[1,0.1]])
# X = np.array([[1,0.1],
# [0.1,1],
# [0.1,0.1],
# [1,1]])
# 标签,也叫真值,1行1列,张三的真值:一定录用
T = np.array([[1]])
# T = np.array([[1],
# [0],
# [0],
# [1]])
# 定义一个2隐层的神经网络:2-2-2-1
# 输入层2个神经元,隐藏1层2个神经元,隐藏2层2个神经元,输出层1个神经元
# 输入层到隐藏层1的权值初始化,2行2列
W1 = np.array([[0.8,0.2],
[0.2,0.8]])
# 隐藏层1到隐藏层2的权值初始化,2行2列
W2 = np.array([[0.5,0.0],
[0.5,1.0]])
# 隐藏层2到输出层的权值初始化,2行1列
W3 = np.array([[0.5],
[0.5]])
# 初始化偏置值
# 隐藏层1的2个神经元偏置
b1 = np.array([[-1,0.3]])
# 隐藏层2的2个神经元偏置
b2 = np.array([[0.1,-0.1]])
# 输出层的1个神经元偏置
b3 = np.array([[-0.6]])
# 学习率设置
lr = 0.1
# 定义训练周期数10000
epochs = 10000
# 每训练1000次计算一次loss值 # 定义测试周期数
report = 1000
# 将所有样本分组,每组大小为
batch_size = 1
# 定义sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# 定义sigmoid函数导数
def dsigmoid(x):
return x*(1-x)
# 更新权值和偏置值
def update():
global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
# 隐藏层1输出
Z1 = np.dot(batch_X,W1) + b1
A1 = sigmoid(Z1)
# 隐藏层2输出
Z2 = (np.dot(A1,W2) + b2)
A2 = sigmoid(Z2)
# 输出层输出
Z3=(np.dot(A2,W3) + b3)
A3 = sigmoid(Z3)
# 求输出层的误差
delta_A3 = (batch_T - A3)
delta_Z3 = delta_A3 * dsigmoid(A3)
# 利用输出层的误差,求出三个偏导(即隐藏层2到输出层的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
# 求隐藏层2的误差
delta_A2 = delta_Z3.dot(W3.T)
delta_Z2 = delta_A2 * dsigmoid(A2)
# 利用隐藏层2的误差,求出三个偏导(即隐藏层1到隐藏层2的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]
delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]
# 求隐藏层1的误差
delta_A1 = delta_Z2.dot(W2.T)
delta_Z1 = delta_A1 * dsigmoid(A1)
# 利用隐藏层1的误差,求出三个偏导(即输入层到隐藏层1的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]
delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]
# 更新权值
W3 = W3 + lr *delta_W3
W2 = W2 + lr *delta_W2
W1 = W1 + lr *delta_W1
# 改变偏置值
b3 = b3 + lr * delta_B3
b2 = b2 + lr * delta_B2
b1 = b1 + lr * delta_B1
# 定义空list用于保存loss
loss = []
batch_X = []
batch_T = []
max_batch = X.shape[0] // batch_size
# 训练模型
for idx_epoch in range(epochs):
for idx_batch in range(max_batch):
# 更新权值
batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
update()
# 每训练5000次计算一次loss值
if idx_epoch % report == 0:
# 隐藏层1输出
A1 = sigmoid(np.dot(X,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
# 计算loss值
print('A3:',A3)
print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A3) / 2))
# 保存loss值
loss.append(np.mean(np.square(T - A3) / 2))
# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,report),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
# 隐藏层1输出
A1 = sigmoid(np.dot(X,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
print('output:')
print(A3)
# 因为最终的分类只有0和1,所以我们可以把
# 大于等于0.5的值归为1类,小于0.5的值归为0类
def predict(x):
if x>=0.5:
return 1
else:
return 0
# map会根据提供的函数对指定序列做映射
# 相当于依次把A2中的值放到predict函数中计算
# 然后打印出结果
print('predict:')
for i in map(predict,A3):
print(i)
实验内容
请回答下列问题:
第一题
1. 如果去掉总裁这一层,相应张三的样本修改为(1.0,0.1,1.0,1.0),分别对应张三的学习成绩、张三的实践成绩、张三的工作能力真值、张三的工作态度真值,代码应该如何修改?
要修改的代码:
-
更改的:
# 求隐藏层2的误差 80. delta_A2 = delta_Z3.dot(batch_T - A2) # 计算loss值 127. print('A2:',A2) 128. print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A2) / 2)) # 保存loss值 130. loss.append(np.mean(np.square(T - A2) / 2)) 145. print(A3) 159. for i in map(predict,A2.T): -
删除的:
# 隐藏层2到输出层的权值初始化,2行1列 27. W3 = np.array([[0.5], 28. [0.5]]) # 输出层的1个神经元偏置 37. b3 = np.array([[-0.6]]) # 输出层输出 68. Z3=(np.dot(A2,W3) + b3) 69. A3 = sigmoid(Z3) # 求输出层的误差 72. delta_A3 = (batch_T - A3) 73. delta_Z3 = delta_A3 * dsigmoid(A3) # 利用输出层的误差,求出三个偏导(即隐藏层2到输出层的权值改变) # 由于一次计算了多个样本,所以需要求平均 76. delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0] 77. delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0] # 更新权值 96. W3 = W3 + lr *delta_W3 # 改变偏置值 101. b3 = b3 + lr * delta_B3 # 输出层输出 125. A3 = sigmoid(np.dot(A2,W3) + b3) # 输出层输出 143. A3 = sigmoid(np.dot(A2,W3) + b3)
第二题
2…如果增加一个样本,李四(0.1,1.0,0),分别对应李四的学习成绩,李四的实践成绩,李四被招聘可能性的真值,代码应该如何修改?此时是一个样本计算一次偏导、更新一次权值,还是两个样本一起计算一次偏导、更新一次权值?(提示:注意 batch_size 的作用)
修改的代码:
5. X = np.array([[1,0.1],
[0.1,1]])
11. T = np.array([[1],
[0]])
结果:
此时,我们通过修改代码:
114. for idx_batch in range(max_batch):
# 更新权值
batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
# 以下为新增的代码
print(batch_X)
print(batch_T)
# 以上为新增的代码
update()
运行程序不难看出:
当batch_size==1时,一个样本计算一次偏导,更新一次权值。
第三题
3.样本为张三[1,0.1,1]、李四[0.1,1,0]、王五[0.1,0.1,0]、赵六[1,1,1],请利用 batch_size 实现教材 279 页提到的“批量梯度下降”、“随机梯度下降”和“小批量梯度下降”,请注意“随机梯度下降”和“小批量梯度下降”要体现随机性。
批量梯度下降
修改代码:
4. # 输入数据4行2列,这里有张三、李四、王五、赵六的数据
X = np.array([[1,0.1],
[0.1,1],
[0.1,0.1],
[1,1]])
# 标签,也叫真值,4行1列,张三的真值:一定录用,李四的真值:一定不录用
T = np.array([[1],
[0],
[0],
[1]])
# batch_size
batch_size = 4
此时,四个样本一起计算一次偏导,更新一次权值,进行一次迭代。符合在每一次迭代时使用所有样本来进行梯度的更新。
随机梯度下降
修改代码:
# 将所有样本分组,每组大小为1
batch_size = 1
114. for idx_batch in range(max_batch):
# 更新权值
# 随机样本
idx_batch = random.randint(0,max_batch-1)
batch_X = X[(idx_batch)*batch_size:(idx_batch+1)*batch_size, :]
batch_T = T[(idx_batch)*batch_size:(idx_batch+1)*batch_size, :]
update()
小批量梯度下降
在这里,我们设置小批量梯度下降的m为2.
修改代码:
# 将所有样本分组,每组大小为
batch_size = 2
for idx_batch in range(max_batch):
# 更新权值
# 随机样本
r_nums = np.array([1,1.5,2])
r_num = random.randint(0,2)
batch_X = X[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
batch_T = T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
update()
第四题
4.【 选 做 】 本 例 中 输 入 向 量 、 真 值 都 是 行 向 量 , 请 将 它 们 修 改 为 列 向 量 , 如X = np.array([[1,0.1]])改为 X = np.array([[1],[0.1]]),请合理修改其它部分以使程序得到与行向量时相同的结果。
基于第三题小批量随机梯度下降更改的代码:
import random
import numpy as np
import matplotlib.pyplot as plt
# 输入数据2行4列
# X = np.array([[1,0.1],[0.1,1],[0.1,0.1],[1,1]])
X = np.array([[1,0.1,0.1,1],
[0.1,1,0.1,1]])
# X = np.array([[1,0.1],
# [0.1,1],
# [0.1,0.1],
# [1,1]])
# 标签,也叫真值,1行4列,张三的真值:一定录用
T = np.array([[1,0,0,1]])
# T = np.array([[1],
# [0],
# [0],
# [1]])
# 定义一个2隐层的神经网络:2-2-2-1
# 输入层2个神经元,隐藏1层2个神经元,隐藏2层2个神经元,输出层1个神经元
# 输入层到隐藏层1的权值初始化,2行2列
W1 = np.array([[0.8,0.2],
[0.2,0.8]])
# 隐藏层1到隐藏层2的权值初始化,2行2列
W2 = np.array([[0.5,0.0],
[0.5,1.0]])
# 隐藏层2到输出层的权值初始化,2行1列
W3 = np.array([[0.5],
[0.5]])
# 初始化偏置值
# 隐藏层1的2个神经元偏置
b1 = np.array([[-1,0.3]])
# 隐藏层2的2个神经元偏置
b2 = np.array([[0.1,-0.1]])
# 输出层的1个神经元偏置
b3 = np.array([[-0.6]])
# 学习率设置
lr = 0.1
# 定义训练周期数10000
epochs = 10000
# 每训练1000次计算一次loss值 # 定义测试周期数
report = 1000
# 将所有样本分组,每组大小为
batch_size = 2
# 定义sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# 定义sigmoid函数导数
def dsigmoid(x):
return x*(1-x)
# 更新权值和偏置值
def update():
global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
# 隐藏层1输出
Z1 = np.dot(batch_X,W1) + b1
A1 = sigmoid(Z1)
# 隐藏层2输出
Z2 = (np.dot(A1,W2) + b2)
A2 = sigmoid(Z2)
# 输出层输出
Z3=(np.dot(A2,W3) + b3)
A3 = sigmoid(Z3)
# 求输出层的误差
delta_A3 = (batch_T - A3)
delta_Z3 = delta_A3 * dsigmoid(A3)
# 利用输出层的误差,求出三个偏导(即隐藏层2到输出层的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
# 求隐藏层2的误差
delta_A2 = delta_Z3.dot(W3.T)
delta_Z2 = delta_A2 * dsigmoid(A2)
# 利用隐藏层2的误差,求出三个偏导(即隐藏层1到隐藏层2的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]
delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]
# 求隐藏层1的误差
delta_A1 = delta_Z2.dot(W2.T)
delta_Z1 = delta_A1 * dsigmoid(A1)
# 利用隐藏层1的误差,求出三个偏导(即输入层到隐藏层1的权值改变) # 由于一次计算了多个样本,所以需要求平均
delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]
delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]
# 更新权值
W3 = W3 + lr *delta_W3
W2 = W2 + lr *delta_W2
W1 = W1 + lr *delta_W1
# 改变偏置值
b3 = b3 + lr * delta_B3
b2 = b2 + lr * delta_B2
b1 = b1 + lr * delta_B1
# 定义空list用于保存loss
loss = []
batch_X = []
batch_T = []
max_batch = X.shape[1] // batch_size
# 训练模型
for idx_epoch in range(epochs):
for idx_batch in range(max_batch):
# 更新权值
# 随机样本
r_nums = np.array([1,1.5,2])
r_num = random.randint(0,2)
batch_X = X.T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
batch_T = T.T[int((r_nums[r_num]-1))*batch_size:(int(r_nums[r_num]))*batch_size]
print(batch_X)
print(batch_T)
update()
# 每训练5000次计算一次loss值
if idx_epoch % report == 0:
# 隐藏层1输出
A1 = sigmoid(np.dot(X.T,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
# 计算loss值
print('A3:',A3)
print('epochs:',idx_epoch,'loss:',np.mean(np.square(T.T - A3) / 2))
# 保存loss值
loss.append(np.mean(np.square(T.T - A3) / 2))
# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,report),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
# 隐藏层1输出
A1 = sigmoid(np.dot(X.T,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
print('output:')
print(A3)
# 因为最终的分类只有0和1,所以我们可以把
# 大于等于0.5的值归为1类,小于0.5的值归为0类
def predict(x):
if x>=0.5:
return 1
else:
return 0
# map会根据提供的函数对指定序列做映射
# 相当于依次把A2中的值放到predict函数中计算
# 然后打印出结果
print('predict:')
for i in map(predict,A3):
print(i)
实验涉及到的实验语法知识
numpy.dot()函数的用法 [1]
numpy.dot(a, b, out=None)
Dot product of two arrays. Specifically,
-
If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).
-
If both a and b are 2-D arrays, it is matrix multiplication, but using
matmulora @ bis preferred. -
If either a or b is 0-D (scalar), it is equivalent to
multiplyand usingnumpy.multiply(a, b)ora * bis preferred. -
If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.
-
If a is an N-D array and b is an M-D array (where
M>=2), it is a sum product over the last axis of a and the second-to-last axis of b:dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])
Examples
>>> np.dot(3, 4)
12
Neither argument is complex-conjugated:
>>> np.dot([2j, 3j], [2j, 3j])
(-13+0j)
For 2-D arrays it is the matrix product:
>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
[2, 2]])
>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128
总结:
- 如果处理的是一维数组,则得到的是两数组的內积
- 如果是二维数组(矩阵)之间的运算,则得到的是矩阵积(mastrix product)
## 一维数组的情况
In : d = np.arange(0,9)
Out: array([0, 1, 2, 3, 4, 5, 6, 7, 8])
In : e = d[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])
In : np.dot(d,e)
Out: 84
##矩阵的情况
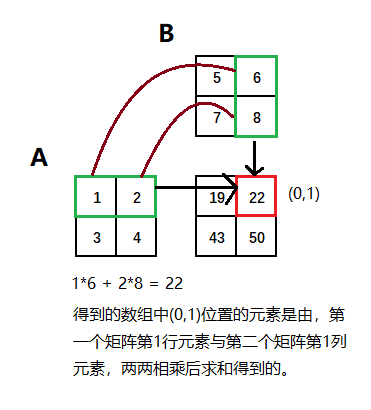
In : a = np.arange(1,5).reshape(2,2)
Out:
array([[1, 2],
[3, 4]])
In : b = np.arange(5,9).reshape(2,2)
Out: array([[5, 6],
[7, 8]])
In : np.dot(a,b)
Out:
array([[19, 22],
[43, 50]])
sigmoid()函数的用法及意义 [2]
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
![]()
这就是sigmoid函数的表达式,这个函数在伯努利分布上非常好用,现在看看他的图像就清楚
![]()
可以看到在趋于正无穷或负无穷时,函数趋近平滑状态,sigmoid函数因为输出范围(0,1),所以二分类的概率常常用这个函数,事实上logistic回归采用这个函数很多教程也说了以下几个优点
1 值域在0和1之间
2 函数具有非常好的对称性
函数对输入超过一定范围就会不敏感
sigmoid的输出在0和1之间,我们在二分类任务中,采用sigmoid的输出的是事件概率,也就是当输出满足满足某一概率条件我们将其划分正类,不同于svm。
代码:
from matplotlib import pyplot as plt
import numpy as np
import math
def sigmoid_function(z):
fz = []
for num in z:
fz.append(1/(1 + math.exp(-num)))
return fz
if __name__ == '__main__':
z = np.arange(-10, 10, 0.01)
fz = sigmoid_function(z)
plt.title('Sigmoid Function')
plt.xlabel('z')
plt.ylabel('σ(z)')
plt.plot(z, fz)
plt.show()
输出函数图像:
![]()
Numpy中的shape函数的用法详解 [3]
摘要
x.shape[0] will give the number of rows in an array. In your case it will give output 10. If you will type x.shape[1], it will print out the number of columns i.e 1024.
详解
中文解释
shape函数的功能是读取矩阵的长度,比如shape[0]就是读取矩阵第一维度的长度,相当于行数。它的输入参数可以是一个整数表示维度,也可以是一个矩阵。shape函数返回的是一个元组,表示数组(矩阵)的维度,例子如下:
- 数组(矩阵)只有一个维度时,shape只有shape[0],返回的是该一维数组(矩阵)中元素的个数,通俗点说就是返回列数,因为一维数组只有一行,一维情况中array创建的可以看做list(或一维数组)
示例代码:
>>> a=np.array([1,2])
>>> a
array([1, 2])
>>> a.shape
(2L,)
>>> a.shape[0]
2L
>>> a.shape[1]
Traceback (most recent call last):
File "" , line 1, in <module>
a.shape[1]
IndexError: tuple index out of range #最后报错是因为一维数组只有一个维度,可以用a.shape或a.shape[0]来访问
- 数组有两个维度(即行和列)时,和我们的逻辑思维一样,a.shape返回的元组表示该数组的行数与列数,请看下例:
示例代码:
>>> a=np.array([[1,2],[3,4]]) #注意二维数组要用()和[]一起包裹起来,键入print a 会得到一个用2个[]包裹的数组(矩阵)
>>> a
array([[1, 2],
[3, 4]])
>>> a.shape
(2L, 2L)
>>> b=np.array([[1,2,3],[4,5,6]])
>>> b
array([[1, 2, 3],
[4, 5, 6]])
>>> b.shape
(2L, 3L)
英文解释
x[0].shape will give the Length of 1st row of an array. x.shape[0] will give the number of rows in an array. In your case it will give output 10. If you will type x.shape[1], it will print out the number of columns i.e 1024. If you would type x.shape[2], it will give an error, since we are working on a 2-d array and we are out of index. Let me explain you all the uses of ‘shape’ with a simple example by taking a 2-d array of zeros of dimension 3x4.
示例代码:
import numpy as np
#This will create a 2-d array of zeroes of dimensions 3x4
x = np.zeros((3,4))
print(x)
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]
#This will print the First Row of the 2-d array
x[0]
array([ 0., 0., 0., 0.])
#This will Give the Length of 1st row
x[0].shape
(4,)
#This will Give the Length of 2nd row, verified that length of row is showing same
x[1].shape
(4,)
#This will give the dimension of 2-d Array
x.shape
(3, 4)
# This will give the number of rows is 2-d array
x.shape[0]
3
# This will give the number of columns is 2-d array
x.shape[1]
3
# This will give the number of columns is 2-d array
x.shape[1]
4
# This will give an error as we have a 2-d array and we are asking value for an index
out of range
x.shape[2]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
<ipython-input-20-4b202d084bc7> in <module>()
----> 1 x.shape[2]
IndexError: tuple index out of range
NumPy 切片和索引 [4]
ndarray对象的内容可以通过索引或切片来访问和修改,与 Python 中 list 的切片操作一样。
ndarray 数组可以基于 0 - n 的下标进行索引,切片对象可以通过内置的 slice 函数,并设置 start, stop 及 step 参数进行,从原数组中切割出一个新数组。
实例:
import numpy as np
a = np.arange(10)
s = slice(2,7,2)
#从索引 2 开始到索引 7 停止,间隔为2
print (a[s])
输出结果为:
[2 4 6]
冒号 : 的解释:如果只放置一个参数,如 [2],将返回与该索引相对应的单个元素。如果为 [2:],表示从该索引开始以后的所有项都将被提取。如果使用了两个参数,如 [2:7],那么则提取两个索引(不包括停止索引)之间的项。
多维数组同样适用上述索引提取方法:
import numpy as np
a = np.array([[1,2,3],
[3,4,5],
[4,5,6]])
print(a)
# 从某个索引处开始切割
print('从数组索引 a[1:] 处开始切割')
print(a[1:])
输出结果为:
[[1 2 3]
[3 4 5]
[4 5 6]]
从数组索引 a[1:] 处开始切割
[[3 4 5]
[4 5 6]]
参考文献:
[1] 越来越胖的GuanRunwei.简述Sigmoid函数(附Python代码)[G/OL].CSDN,2019(2019-11-25).https://blog.csdn.net/qq_38890412/article/details/103246057
[2] 付修磊.Numpy中的shape函数的用法详解[G/OL].CSDN,2018(2018-01-17).https://blog.csdn.net/qq_38669138/article/details/79084275
[3] Animesh Johri.x.shape[0] vs x[0].shape in NumPy[G/OL].stackoverflow,2018(2018-9-22).https://stackoverflow.com/questions/48134598/x-shape0-vs-x0-shape-in-numpy
[4] RUNOOB.COM编者.NumPy 切片和索引[G/OL].RUNOOB.COM,2021…https://www.runoob.com/numpy/numpy-indexing-and-slicing.html