Deep Global Registration (CVPR 2020) 论文解析

0. 相关链接：

• 论文网址：https://node1.chrischoy.org/data/publications/dgr/DGR.pdf
• 论文代码：https://github.com/chrischoy/DeepGlobalRegistration
• 论文视频：https://youtu.be/stzgn6DkozA

1. 简介

\qquad Deep Global Registration (DGR) 是一个基于correspondence的partial-to-partial registration通用框架，和之前我写的Fast Global Registration的框架有类似之处，都是在原有correspondence的基础上，采用outlier filter策略取得可靠的inliers，再在inliers的基础上使用SVD得到鲁棒的transformation. 请注意这种outlier filter的操作不需要重复求取correspondence（与ICP不同）的，而只是每次滤除一部分不可靠的correspondence。与FGR的不同主要有以下两点：

1. FGR采用关联验证+BR对偶性进行滤波，而DGR采用流形学习+Weighted Procrustes+Robust Refinement过程进行滤波
2. FGR采用FPFH作为特征输入，DGR采用FCGF作为特征输入。FCGF是一种稀疏卷积编码的深度特征，在3DMatch上有较高的召回率。

\qquad 接下来分以下几步介绍DGR：稀疏卷积与特征提取，Weighted Procrustes与流形学习，Robust Refinement过程。整体的理解难度是要低于FGR的。

2. 稀疏卷积与特征提取

\qquad 稀疏卷积的详细介绍见NVIDA发布的两个链接：代码实现、理论解析。采用的库是NVIDA的MinkowskiEgine。这里只简单介绍一下它与不同的卷积有什么不同。
\qquad 稀疏卷积（Sparse Convoluntion）是用于点云的一种卷积。由于点云的坐标是浮点数，因此一般会一步操作将点云的坐标离散化（Quantization），离散化后的点云坐标为整数，符合卷积核的计算规范。
\qquad 稀疏卷积张量（Sparse Tensor）的保存规范是坐标和特征分别保存。因为稀疏张量的坐标不满足Dense的特征。本文就batch=1的情况讨论，C的每行保存一个D维坐标向量，而F的每行保存一个$F_D$维的特征向量（在下图中没展示出来）。C的每一行对应F的一个特征，而C不包含的坐标在F中一律记为0。

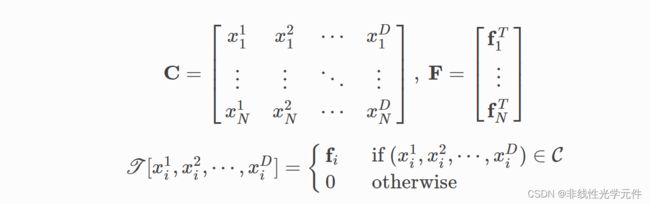
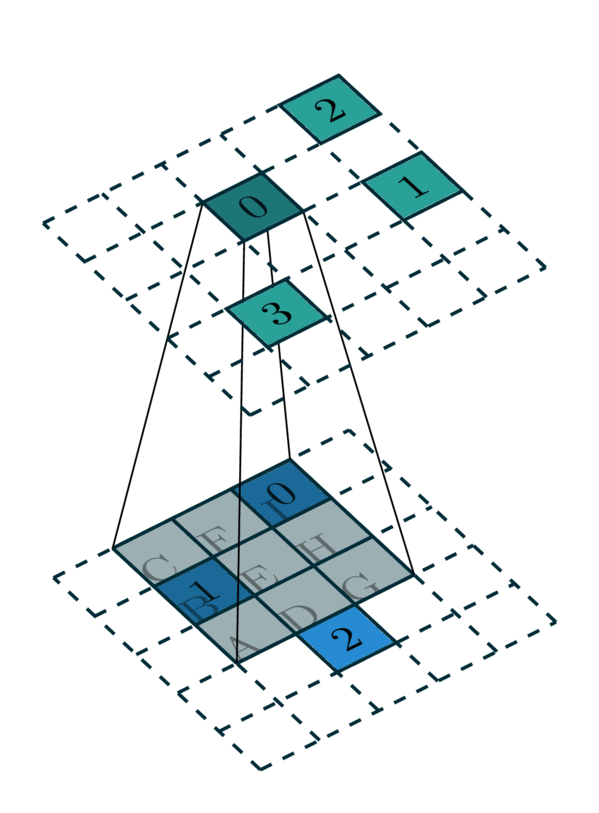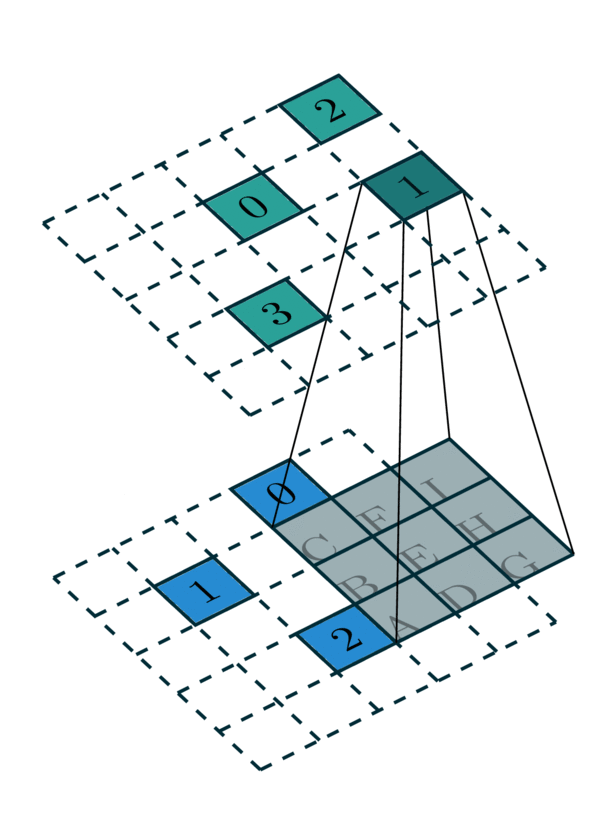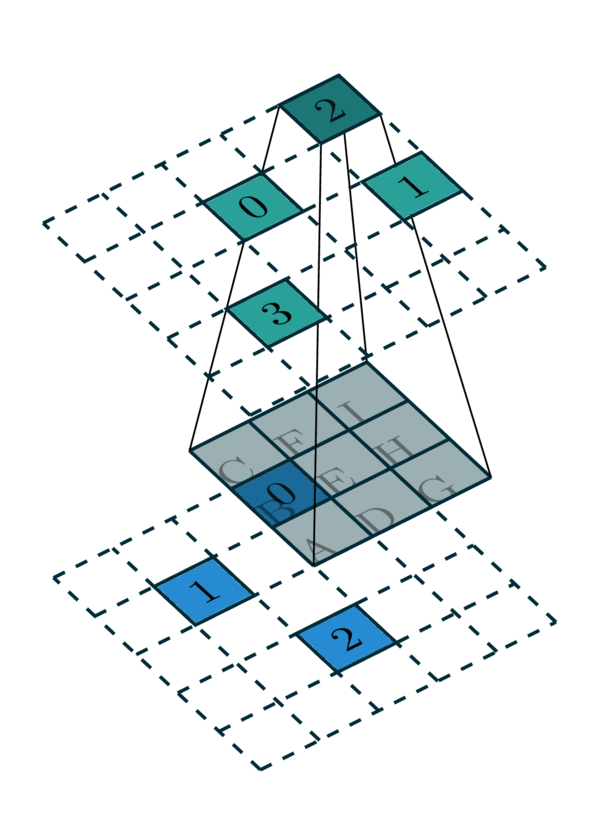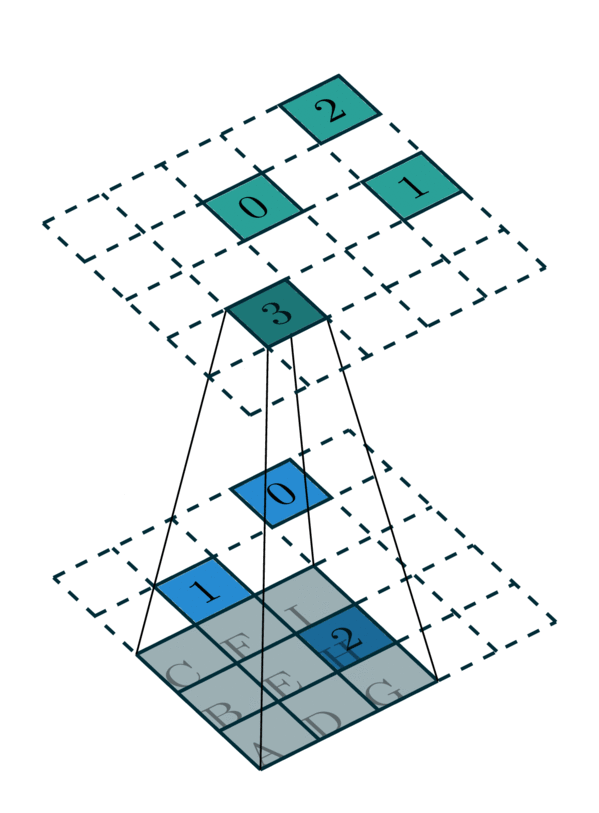
\qquad 对于一个3x3的稀疏卷积操作而言，需要知道它周围包含自身的9个邻域（一般需要由搜索器事先确定），然后在使用3x3卷积与它周围邻域的值做乘法即可。稀疏卷积的stride和普通卷积类似。

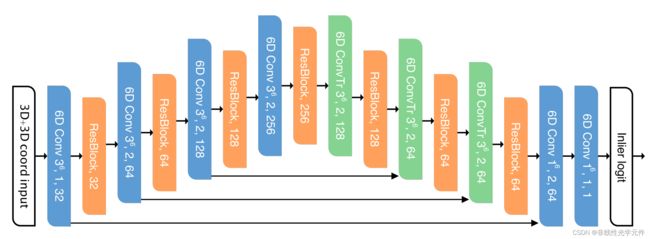
\qquad DGR的特征提取层使用的是FCGF（Fully Convolutional Geometric Feature），FCGF是稀疏卷积版的ResUNet结构，是一种32维度的端到端点云特征，在3DMatch上有93%-96%的Recall（不同Voxel和Final Feature），它的结构表示如下。
DGR在使用FCGF时的匹配是基于简单的L2范数距离的（这一点与FGR类似），采用KDTree进行加速。

3. Weighted Procrustes与流形学习

\qquad 读过ICP那篇论文的学者应该知道以下问题存在闭解：
$$\arg \underset{\text{R},\text{t}}{\min }\sum _i\Vert y_i-\text{R}{x}_i+\text{t}{\Vert }_2$$
\qquad DGR的作者找到了一篇1991年的论文，它证明了即使加上了权重$w_i$，上述问题也存在闭解，即
$$\arg \underset{\text{R},\text{t}}{\min }\sum _i{w}_i\Vert y_i-\text{R}{x}_i+\text{t}{\Vert }_2$$
这个闭解的形式论文和代码中都有，我将代码放在下面作为参考：

def weighted_procrustes(X:torch.Tensor, Y:torch.Tensor, w:torch.Tensor, eps:float):
	  """
	  X: torch tensor N x 3
	  Y: torch tensor N x 3
	  w: torch tensor N
	  """
	  # https://ieeexplore.ieee.org/document/88573
	  assert len(X) == len(Y)
	  W1 = torch.abs(w).sum()
	  w_norm = w / (W1 + eps)
	  mux = (w_norm * X).sum(0, keepdim=True)
	  muy = (w_norm * Y).sum(0, keepdim=True)
	
	  # Use CPU for small arrays
	  Sxy = (Y - muy).t().mm(w_norm * (X - mux)).cpu().double()
	  U, D, V = Sxy.svd()
	  S = torch.eye(3).double()
	  if U.det() * V.det() < 0:
	    S[-1, -1] = -1
	
	  R = U.mm(S.mm(V.t())).float()
	  t = (muy.cpu().squeeze() - R.mm(mux.cpu().t()).squeeze()).float()
	  return R, t

\qquad 得到这个闭解的好处也很明显，$w_i$权重可以理解为每一组匹配的置信度，这样就可以针对软匹配进行SVD求解了。而这个置信度$w_i$也稀疏卷积的端到端网络通过流行学习得到的。
\qquad 例如A={0,1,2,3,4,5}, B={5,6,7,8,9,10}，假设A和B的一组匹配关系为{(0,5),(1,6),(2,7),(3,9),(4,8),(5,10)}。那么匹配{(0,5),(1,6),(2,7),(5,10)}就分布在2D平面的一个1D流形上，而错误匹配(3,9),(4,8)则不在。将这个结论拓展到三维匹配。例如$A=\{(x_1^1,x_2^1,x_3^1),(x_1^2,x_2^2,x_3^2),...,(x_1^n,x_2^n,x_3^n)\}$, $B=\{(y_1^1,y_2^1,y_3^1),(y_1^2,y_2^2,y_3^2),...,(y_1^n,y_2^n,y_3^n)\}$，若将A和B的一组匹配的坐标也像上述一样合并在一起，那么它们应该分布在6D空间的一个3D流形上。因为它们应该满足一个三自由度方程：
$$y_i=\text{R}{x}_i+\text{t}$$
这种流形判据也就是点云配准中常说的inlier prediction.
\qquad 作者仍然采用了稀疏卷积来预测这些匹配是不是分布在流形上，由于分布在流形上的判据通常是由它周围的点确定的，因此这种做法也许是可行的（但作者没有证明了）。
\qquad 可以将流形学习理解为分割模型，最后一维度置为1维表示是否在流形上的概率，则得到了一个6D空间上的流形学习稀疏卷积网络（如下）。
\qquad 这个网络被作者称为SimpleUNet，但实际上和ResUNet的结构非常相似，不同在于卷积编码的维度，还有就是上面FCGF的ResUNet是3D卷积，这个SimpleUNet是6D卷积。
\qquad 续上前节的FCGF特征匹配，DGR的结构就是先提取FCGF特征，利用KDTree搜索L2范数最小完成初步匹配，对初步匹配结果利用SimpleUNet预测inlier prediction，得到每一个匹配的权重$w_i$，最后利用weighted procrustes得到R和t的闭解。
\qquad 代码中还有一个小tips，inlier prediction会输出一个浮点数，这个浮点数会先经过Sigmoid层得到一个0~1的数。作者给出了个阈值$ϵ$用于将$<ϵ$的所有prediction置0。

4. Robust Refinement

\qquad 看到这里是不是觉得DGR已经结束了，已经得到$\text{R}$和$\text{t}$了。然而作者增加了Robust Refinement，然后利用torch自带的优化器进行梯度下降优化（代码中设置最大iteration为1000）。这一步的目的还是为了减小outlier产生的不良影响。
\qquad 设第3节产生的初始旋转矩阵和平移向量为$R_0,T_0$，Template点云为$P_1$，source点云为$P_0$。为了优化变量的方便，采用李群的变量形式定义优化变量，即设$R=\mathcal{G}({\xi }_R)$，${\xi }_T=R^{-1}T$，则得到了一下问题的优化形式：
$$\arg \underset{{\xi }_R,{\xi }_T}{\min }\sum _i\varphi (w)L(R{p}_1+T-p_0)$$
其中$\varphi (w)=\{\begin{array}{ll}w,& w>\tau \\ 0,& w\le \tau \end{array}$,$L(x)=\{\begin{array}{ll}0.5x^2,& x<1\\ 0.5(|x|-0.5).& x\ge 1\end{array}$
其中HuberLoss $L(x)$(有时也称为Smooth L1Loss)的图像大致如下：

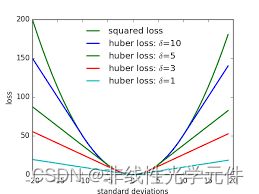
\qquad 上述的1是指1个voxel。由于HuberLoss可微，所以作者设的$R=R_0,T=T_0$，通过迭代和梯度下降的方法对$R，T$进行进一步优化，从而满足HuberLoss最小，这一步其实也是具有启发性，采用梯度优化主要还是为了追求效率，也是一个启发式的idea。相关代码如下

transformation = Transformation(R, t).to(points.device)

  optimizer = optim.Adam(transformation.parameters(), lr=1e-1)
  scheduler = optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.999)
  loss_prev = loss_fn(transformation(points), trans_points).item()
  break_counter = 0

  # Transform points
  for i in range(max_iter):
    new_points = transformation(points)  # R,t are learnable paramters
    loss = loss_fn(new_points, trans_points)  # loss is weighted least square function
    if loss.item() < 1e-7:
      break

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()  # optimize R and t
    scheduler.step()
    if i % stat_freq == 0 and verbose:
      print(i, scheduler.get_lr(), loss.item())

    if abs(loss_prev - loss.item()) < loss_prev * break_threshold_ratio:
      break_counter += 1
      if break_counter >= max_break_count:
        break

    loss_prev = loss.item()

它在3DMatch和KITTI上的效果如下表

实际上，这个结果是在成功样本率中的performance而非全部样本的performance，筛选的标准是<0.6m and <5°，DGR的成功率在KITTI数据集上为98.38%，全局的样本误差为RTE=0.15m，RRE=1.43°，算法平均耗时0.60s（在3080Ti上测试）.