代码随想录1刷—二叉树篇(二)
代码随想录1刷—二叉树篇(二)
-
-
- 迭代法中究竟什么时候用队列,什么时候用栈?
- 递归函数什么时候要有返回值,什么时候不能有返回值?
- [222. 完全二叉树的节点个数](https://leetcode.cn/problems/count-complete-tree-nodes/)
-
- 普通二叉树的求法
- 利用完全二叉树性质的求法
- [110. 平衡二叉树](https://leetcode.cn/problems/balanced-binary-tree/)
- [257. 二叉树的所有路径](https://leetcode.cn/problems/binary-tree-paths/)(认真多看几次!总会做出来的!)
-
- 递归
- 迭代
- [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/)
- [513. 找树左下角的值](https://leetcode.cn/problems/find-bottom-left-tree-value/)
- [112. 路径总和](https://leetcode.cn/problems/path-sum/)
- [113. 路径总和 II](https://leetcode.cn/problems/path-sum-ii/)
- [106. 从中序与后序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)
- [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
- [654. 最大二叉树](https://leetcode.cn/problems/maximum-binary-tree/)
-
- 什么时候递归函数前面加if,什么时候不加if?
- [617. 合并二叉树](https://leetcode.cn/problems/merge-two-binary-trees/)
- [700. 二叉搜索树中的搜索](https://leetcode.cn/problems/search-in-a-binary-search-tree/)
-
-
- 迭代法
-
- [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/)
- [530. 二叉搜索树的最小绝对差](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)
- [501. 二叉搜索树中的众数](https://leetcode.cn/problems/find-mode-in-binary-search-tree/)
-
- 如果不是二叉搜索树
-
- map中的value排序问题
- 是二叉搜索树
-
-
- 递归法
- 迭代法
-
-
迭代法中究竟什么时候用队列,什么时候用栈?
如果是模拟前中后序遍历就用栈,如果是适合层序遍历就用队列;
其他情况:先用队列试试行不行,不行就用栈。
递归函数什么时候要有返回值,什么时候不能有返回值?
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(113. 路径总和 II)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (236. 二叉树的最近公共祖先)
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(112. 路径总和)
222. 完全二叉树的节点个数
普通二叉树的求法
遍历+记录遍历的节点数量就可以了。
//递归
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
时间复杂度:O(n)
空间复杂度:O(log n),算上了递归系统栈占用的空间
//迭代
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录节点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
时间复杂度:O(n)
空间复杂度:O(n)
利用完全二叉树性质的求法
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
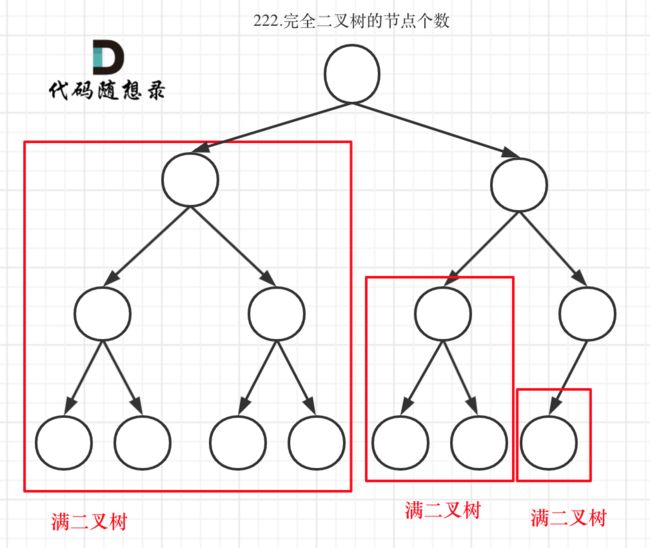
完全二叉树(二)如图:

可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftHeight++;
}
while (right) { // 求右子树深度
right = right->right;
rightHeight++;
}
if (leftHeight == rightHeight) {
return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2,所以leftHeight初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
时间复杂度:O(log n × log n)
空间复杂度:O(log n)
110. 平衡二叉树
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
强调一波概念:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
关于根节点的深度究竟是1 还是 0:leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,暂时以leetcode为准(毕竟在这上面刷题)。
class Solution {
public:
int getHeight(TreeNode* node) {
if (node == nullptr) return 0;
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1+max(leftHeight, rightHeight);
//abs()绝对值 //返回以该节点为根节点的二叉树的高度
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};
迭代版本太复杂了干不明白,代码随想录链接:迭代版平衡二叉树解法 (programmercarl.com)
257. 二叉树的所有路径(认真多看几次!总会做出来的!)
递归
class Solution {
public:
vector<string> answer;
vector<int> path;
void traversal(TreeNode* cur,vector<int>& path,vector<string>& answer){
path.push_back(cur->val);
if(cur->left == nullptr && cur->right == nullptr){
string sPath;
for(int i = 0;i < path.size() - 1;i++){
sPath += to_string(path[i]);
//to_string函数 : 将数值转化为字符串。返回对应的字符串
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
answer.push_back(sPath);
return;
}
if(cur->left){
traversal(cur->left,path,answer);
path.pop_back();
}
if(cur->right){
traversal(cur->right,path,answer);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
if(root == nullptr) return answer;
traversal(root,path,answer);
return answer;
}
};
精简版的递归我没看懂emm…点击跳转看吧:二叉树所有路径(递归版)—代码随想录 (programmercarl.com)
迭代
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> TreeSt;
stack<string> pathSt;
vector<string> result;
if(root == nullptr) return result;
TreeSt.push(root);
pathSt.push(to_string(root->val));
while(!TreeSt.empty()){
TreeNode* node = TreeSt.top();
TreeSt.pop();
string path = pathSt.top();
pathSt.pop();
if(node->left == nullptr && node->right == nullptr){
result.push_back(path);
}
if(node->left){
TreeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
if(node->right){
TreeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
}
return result;
}
};
404. 左叶子之和
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == nullptr) return 0;
int val = 0;
if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr){
val += root->left->val;
}
return val + sumOfLeftLeaves(root->right) + sumOfLeftLeaves(root->left);
}
};
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode*> stack;
if(root == nullptr) return 0;
stack.push(root);
int result = 0;
while(!stack.empty()){
TreeNode* node = stack.top();
stack.pop();
if(node->left!=nullptr&&node->left->left==nullptr&&node->left->right==nullptr){
result += node->left->val;
}
if(node->right) stack.push(node->right);
if(node->left) stack.push(node->left);
}
return result;
}
};
513. 找树左下角的值
注意!左下角!是最底层 最左边!所以用层序遍历到最底层!层序遍历的话要用队列!
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if(root != nullptr) que.push(root);
int result = 0;
while(!que.empty()){
int size = que.size();
for(int i = 0; i< size ;i++){
TreeNode* node = que.front();
que.pop();
if(i == 0) result = node->val;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return result;
}
};
class Solution {
public:
int maxLen = INT_MIN;
int leftval;
void traversal(TreeNode* root,int leftLen){
if(root->left == nullptr && root->right == nullptr){
if(leftLen > maxLen){
maxLen = leftLen;
leftval = root->val;
}
return;
}
if(root->left){
traversal(root->left, leftLen + 1);
}
if(root->right){
traversal(root->right, leftLen + 1);
}
return;
}
int findBottomLeftValue(TreeNode* root) {
traversal(root,0);
return leftval;
}
};
112. 路径总和
class Solution {
public:
bool traversal(TreeNode* cur, int sum){
if(!cur->left &&!cur->right && sum == 0) return true;
if(!cur->left &&!cur->right && sum != 0 ) return false;
if(cur->left){
if(traversal(cur->left,sum - cur->left->val)) return true;
}
if(cur->right){
if(traversal(cur->right,sum - cur->right->val)) return true;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr) return false;
return traversal(root,targetSum - root->val);
}
};
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) return false;
if (!root->left && !root->right && targetSum == root->val) {
return true;
}
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
}; //超简版递归
//迭代版本
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root==nullptr) return false;
stack<pair<TreeNode*,int>> st;
st.push(pair<TreeNode*,int>(root,root->val));
while(!st.empty()){
pair<TreeNode*, int> node = st.top();
st.pop();
if (!node.first->left && !node.first->right && targetSum == node.second) return true;
if (node.first->left){
st.push(pair<TreeNode*, int>(node.first->left, node.second + node.first->left->val));
}
if (node.first->right){
st.push(pair<TreeNode*, int>(node.first->right, node.second + node.first->right->val));
}
}
return false;
}
};
113. 路径总和 II
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) {
result.push_back(path);
return;
}
if (!cur->left && !cur->right && count != 0) return ;
if (cur->left) { // 左 (空节点不遍历)
path.push_back(cur->left->val);
traversal(cur->left, count - cur->left->val); // 递归
path.pop_back();
}
if (cur->right) { // 右 (空节点不遍历)
path.push_back(cur->right->val);
traversal(cur->right, count - cur->right->val); // 递归
path.pop_back();
}
return ;
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
result.clear();
path.clear();
if (root == nullptr) return result;
path.push_back(root->val); // 把根节点放进路径
traversal(root, targetSum - root->val);
return result;
}
};
106. 从中序与后序遍历序列构造二叉树

//数组版本,每层递归定定义了新的vector(就是数组),既耗时又耗空间
class Solution {
public:
TreeNode* traversal(vector<int>& inorder,vector<int>& postorder){
if(postorder.size() == 0) return nullptr;
int rootvalue = postorder[postorder.size() - 1];
TreeNode* Root = new TreeNode(rootvalue);
if(postorder.size() == 1) return Root;
int CutIndex;
for(CutIndex = 0;CutIndex < inorder.size();CutIndex++){
if(inorder[CutIndex] == rootvalue) break;
}
vector<int> leftInorder(inorder.begin(),inorder.begin() + CutIndex);
vector<int> rightInorder(inorder.begin() + CutIndex + 1,inorder.end());
postorder.resize(postorder.size() - 1);
vector<int> leftPostorder(postorder.begin(),postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(),postorder.end());
Root->left = traversal(leftInorder,leftPostorder);
Root->right = traversal(rightInorder,rightPostorder);
return Root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0 || postorder.size() == 0) return nullptr;
return traversal(inorder,postorder);
}
};
//索引下标版本 思路和前面一样 但是不用重复定义vector了
class Solution {
public:
TreeNode* traversal(vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if(postorderBegin == postorderEnd) return nullptr;
int rootvalue = postorder[postorderEnd - 1];
TreeNode* Root = new TreeNode(rootvalue);
if(postorderEnd - postorderBegin == 1) return Root;
int CutIndex;
for(CutIndex = 0;CutIndex < inorder.size();CutIndex++){
if(inorder[CutIndex] == rootvalue) break;
}
int leftInorderBegin = inorderBegin;
int leftInorderEnd = CutIndex;
int rightInorderBegin = CutIndex + 1;
int rightInorderEnd = inorderEnd;
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + CutIndex - inorderBegin;
int rightPostorderBegin = postorderBegin + CutIndex - inorderBegin;
int rightPostorderEnd = postorderEnd - 1;
Root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
Root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return Root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0 || postorder.size() == 0) return nullptr;
return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());
}
};
105. 从前序与中序遍历序列构造二叉树
class Solution {
public:
TreeNode* traversal(vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if(postorderBegin == postorderEnd) return nullptr;
int rootvalue = postorder[postorderBegin];
TreeNode* Root = new TreeNode(rootvalue);
if(postorderEnd - postorderBegin == 1) return Root;
int CutIndex;
for(CutIndex = 0;CutIndex < inorder.size();CutIndex++){
if(inorder[CutIndex] == rootvalue) break;
}
int leftInorderBegin = inorderBegin;
int leftInorderEnd = CutIndex;
int rightInorderBegin = CutIndex + 1;
int rightInorderEnd = inorderEnd;
int leftPostorderBegin = postorderBegin + 1;
int leftPostorderEnd = postorderBegin + 1 + CutIndex - inorderBegin;
int rightPostorderBegin = postorderBegin + 1 + CutIndex - inorderBegin;
int rightPostorderEnd = postorderEnd;
Root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
Root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return Root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
654. 最大二叉树
//也是每层递归定定义了新的vector(就是数组),既耗时又耗空间
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
//题干说了1 <= nums.length <= 1000 所以不会是空
//当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了,那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
TreeNode* node = new TreeNode(0);
if(nums.size() == 1){
node->val = nums[0];
return node;
}
//找到最大值和其对应的下标
int MaxValue = 0;
int MaxValueIndex = 0;
for(int i = 0 ;i < nums.size();i++){
if(nums[i] > MaxValue){
MaxValue = nums[i];
MaxValueIndex = i;
}
}
node->val = MaxValue;
//最大值所在的下标左区间 构造左子树
if(MaxValueIndex > 0){
vector<int> newVector(nums.begin(), nums.begin() + MaxValueIndex);
node->left = constructMaximumBinaryTree(newVector);
}
//最大值所在的下标左区间 构造左子树
if(MaxValueIndex < (nums.size() - 1)){
vector<int> newVector(nums.begin() + MaxValueIndex + 1,nums.end());
node->right = constructMaximumBinaryTree(newVector);
}
return node;
}
};
class Solution {
public:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left >= right) return nullptr;
int maxValueIndex = left;
for (int i = left + 1; i < right; i++) {
if (nums[i] > nums[maxValueIndex]){
maxValueIndex = i;
}
}
TreeNode* root = new TreeNode(nums[maxValueIndex]);
root->left = traversal(nums, left, maxValueIndex);
root->right = traversal(nums, maxValueIndex + 1, right);
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums, 0, nums.size());
}
};
注意类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
什么时候递归函数前面加if,什么时候不加if?
其实就是不同代码风格的实现,一般情况来说:如果让空节点(空指针)进入递归,就不加if,如果不让空节点进入递归,就加if限制一下,相应的两者的终止条件也会有相应的调整。
在本题目中给的两个版本:
第一版递归过程:(加了if判断,为了不让空节点进入递归)
if (maxValueIndex > 0) { // 这里加了判断是为了不让空节点进入递归 vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex); node->left = constructMaximumBinaryTree(newVec); } if (maxValueIndex < (nums.size() - 1)) { // 这里加了判断是为了不让空节点进入递归 vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end()); node->right = constructMaximumBinaryTree(newVec); }第二版递归过程: (如下代码就没有加if判断)
root->left = traversal(nums, left, maxValueIndex); root->right = traversal(nums, maxValueIndex + 1, right);第二版代码是允许空节点进入递归,所以没有加if判断,当然终止条件也要有相应的改变。
第一版终止条件,是遇到叶子节点就终止,因为空节点不会进入递归。
第二版相应的终止条件,是遇到空节点,也就是数组区间为0,就终止了。
617. 合并二叉树
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 == nullptr) return root2;
if(root2 == nullptr) return root1;
TreeNode* node = new TreeNode(0);
node->val = root1->val + root2->val;
node->left = mergeTrees(root1->left,root2->left);
node->right = mergeTrees(root1->right,root2->right);
return node;
}
};
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 == nullptr) return root2;
if(root2 == nullptr) return root1;
queue<TreeNode*> que;
que.push(root1);
que.push(root2);
while(!que.empty()){
TreeNode* node1 = que.front();que.pop();
TreeNode* node2 = que.front();que.pop();
node1->val += node2->val;
if(node1->left != nullptr && node2->left != nullptr){
que.push(node1->left);
que.push(node2->left);
}
if(node1->right != nullptr && node2->right != nullptr){
que.push(node1->right);
que.push(node2->right);
}
if(node1->left == nullptr && node2->left != nullptr){
node1->left = node2->left;
}
if(node1->right == nullptr && node2->right != nullptr){
node1->right = node2->right;
}
}
return root1;
}
};
700. 二叉搜索树中的搜索
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (root == nullptr || root->val == val)
return root;
if (root->val > val)
return searchBST(root->left, val);
if (root->val < val)
return searchBST(root->right, val);
return NULL;
}
};
迭代法
一提到二叉树遍历的迭代法,可能立刻想起使用栈来模拟深度遍历,使用队列来模拟广度遍历。对于二叉搜索树可就不一样了,因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树,递归过程中还有回溯的过程,例如走一个左方向的分支走到头了,那么要调头,在走右分支。而对于二叉搜索树,不需要回溯的过程,因为节点的有序性就帮我们确定了搜索的方向。
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while (root != nullptr) {
if (root->val > val)
root = root->left;
else if (root->val < val)
root = root->right;
else return root;
}
return NULL;
}
};
98. 验证二叉搜索树
中序遍历下,输出的二叉搜索树节点的数值是有序序列。有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。
class Solution {
public:
vector<int> vec;
void tracersal(TreeNode* root){
if(root == nullptr) return;
tracersal(root->left);
vec.push_back(root->val);
tracersal(root->right);
} //前序遍历放入数组
bool isValidBST(TreeNode* root) {
vec.clear();
tracersal(root);
for(int i = 1;i < vec.size();i++){
if(vec[i] <= vec[i - 1])
return false;
}
return true;
}
};
class Solution {
public:
TreeNode* pre = nullptr; //用于记录前一个结点
bool isValidBST(TreeNode* root) {
if(root == nullptr) return true;
bool left = isValidBST(root->left);
if(pre != nullptr && pre->val >= root->val)
return false;
pre = root; //记录结点~
bool right = isValidBST(root->right);
return left && right;
}
};
530. 二叉搜索树的最小绝对差
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root){
if(root == nullptr) return;
traversal(root->left);
vec.push_back(root->val);
traversal(root->right);
}
public:
int getMinimumDifference(TreeNode* root) {
vec.clear();
traversal(root);
if(vec.size() < 2) return 0;
int result = INT_MAX;
for(int i = 1; i < vec.size();i++){
result = min(result,vec[i] - vec[i-1]);
}
return result;
}
};
class Solution {
private:
int result = INT_MAX;
TreeNode* pre;
void traversal(TreeNode* cur){
if(cur == nullptr) return;
traversal(cur->left);
if(pre != nullptr){
result = min(result,cur->val - pre->val);
}
pre = cur; //在递归中记录前一个节点的指针
traversal(cur->right);
}
public:
int getMinimumDifference(TreeNode* root) {
traversal(root);
return result;
}
};
//迭代法
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = nullptr;
int result = INT_MAX;
while(cur != nullptr || !st.empty()){
if(cur != nullptr){
st.push(cur);
cur = cur->left; //左
}else{
cur = st.top();
st.pop();
if(pre != nullptr){ //中
result = min(result,cur->val - pre->val);
}
pre = cur;
cur = cur->right; //右
}
}
return result;
}
};
501. 二叉搜索树中的众数
如果不是二叉搜索树
把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
class Solution {
private:
void searchBST(TreeNode* cur,unordered_map<int,int>& map){
if(cur == nullptr)
return;
map[cur->val]++;
searchBST(cur->left,map);
searchBST(cur->right,map);
return;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map; // key:元素,value:出现频率
vector<int> result;
if(root == nullptr)
return result;
searchBST(root, map);
vector<pair<int,int>> vec(map.begin(),map.end());
sort(vec.begin(),vec.end(),cmp);
result.push_back(vec[0].first); //最高的就是答案
for(int i = 1;i<vec.size();i++){
if(vec[i].second == vec[0].second) //可能最高的不止一个,继续放
result.push_back(vec[i].first);
else break;
}
return result;
}
};
map中的value排序问题
注意:无法直接对map中的value排序,C++中如果使用std::map或者std::multimap,那么可以对key排序,但不能对value排序。
所以要把map转化数组即vector,再进行排序,当然vector里面放的也是pair类型的数据,第一个int为元素,第二个int为出现频率。
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second; // 按照频率从大到小排序
}
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
是二叉搜索树
递归法
class Solution {
private:
int maxCount;
int count;
TreeNode* pre;
vector<int> result;
void searchBST(TreeNode* cur){
if(cur == nullptr)
return;
searchBST(cur->left);
if(pre == nullptr){
count = 1;
}else if(pre->val == cur->val){
count++;
}else{
count = 1;
}
pre = cur;
if(count == maxCount){
result.push_back(cur->val); //由于众数不止一个所以需要二次遍历
//而直接将其加入数组中可以规避二次便利
} //但是并无法确定此时的maxCount为最大的,因此需要下面的步骤
if(count > maxCount){
maxCount = count;
result.clear();
result.push_back(cur->val);
}
searchBST(cur->right);
return;
}
public:
vector<int> findMode(TreeNode* root) {
count = 0;
maxCount = 0;
TreeNode* pre = nullptr;
result.clear();
searchBST(root);
return result;
}
};
迭代法
class Solution {
public:
vector<int> findMode(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = nullptr;
int maxCount = 0;
int count = 0;
vector<int> result;
while (cur != nullptr || !st.empty()) {
if (cur != nullptr) {
st.push(cur);
cur = cur->left; // 左
} else {
cur = st.top();
st.pop(); // 中
if(pre == nullptr){
count = 1;
}else if(pre->val == cur->val){
count++;
}else{
count = 1;
}
pre = cur;
if(count == maxCount){
result.push_back(cur->val);
}
if(count > maxCount){
maxCount = count;
result.clear();
result.push_back(cur->val);
}
cur = cur->right; // 右
}
}
return result;
}
};