【机器学习】自动编码器

自动编码器

简介：

自动编码器是一种无监督的神经网络模型，它可以学习到输入数据的隐含特征，这称为编码(coding)，同时用学习到的新特征可以重构出原始输入数据，称之为解码(decoding)。从直观上来看，自动编码器可以用于特征降维，类似主成分分析PCA，但是其相比PCA其性能更强，这是由于神经网络模型可以提取更有效的新特征。除了进行特征降维，自动编码器学习到的新特征可以送入有监督学习模型中，所以自动编码器可以起到特征提取器的作用。作为无监督学习模型，自动编码器还可以用于生成与训练样本不同的新数据，这样自动编码器（变分自动编码器，Variational Autoencoders）就是生成式模型。

自动编码器原理

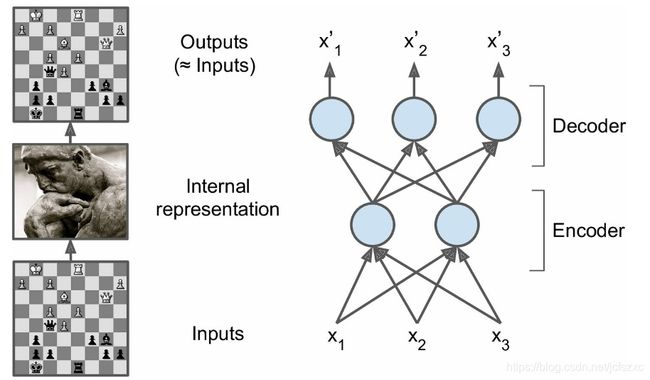
自动编码器的基本结构如图1所示，包括编码和解码两个过程：

自动编码器是将输入x进行编码得到新的特征Y，并且希望原始的输入X能够从新特征Y重构出来。编码过程如下：
$$y=f(Wx+b)$$

可以看到，和神经网络的结构一样，其编码就是线性组合之后加上非线性的激活函数。如果没有非线性的包装，那么自动编码器就和普通的PCA没有本质区别了。利用新的特征 Y，可以对输入X重构，即解码过程：
$$x^{\prime }=f(W^{\prime }x+b^{\prime })$$

我们希望重构出的x’和x尽可能一致，可以采用最小化负对数似然的损失函数来训练这个模型：
$$L=-LogP(x|x^{\prime })$$

对于高斯分布的数据，采用均方误差就好，而对于伯努利分布可以采用交叉熵，这个是可以根据似然函数推导出来的。一般情况下，我们会对自动编码器加上一些限制，常用的是使$W^{\prime }=W^T$，这称为绑定权重（tied weights），本文所有的自动编码器都加上这个限制。有时候，我们还会给自动编码器加上更多的约束条件，去噪自动编码器以及稀疏自动编码器就属于这种情况，因为大部分时候单纯地重构原始输入并没有什么意义，我们希望自动编码器在近似重构原始输入的情况下能够捕捉到原始输入更有价值的信息。

堆栈自动编码器

前面我们讲了自动编码器的原理，不过所展示的自动编码器只是简答的含有一层，其实可以采用更深层的架构，这就是堆栈自动编码器或者深度自动编码器，本质上就是增加中间特征层数。这里我们以MNIST数据为例来说明自动编码器，建立两个隐含层的自动编码器，如图2所示：

对于MNIST来说，其输入是28*28=784维度的特征，这里使用了两个隐含层其维度分别为300和150，可以看到是不断降低特征的维度了。得到的最终编码为150维度的特征，使用这个特征进行反向重构得到重建的特征，我们希望重建特征和原始特征尽量相同。由于MNIST是0,1量，可以采用交叉熵作为损失函数，TF的代码核心代码如下：

n_inputs = 28*28
n_hidden1 = 300
n_hidden2 = 150

# 定义输入占位符：不需要y
X = tf.placeholder(tf.float32, [None, n_inputs])

# 定义训练参数
initializer = tf.contrib.layers.variance_scaling_initializer()
W1 = tf.Variable(initializer([n_inputs, n_hidden1]), name="W1")
b1 = tf.Variable(tf.zeros([n_hidden1,]), name="b1")
W2 = tf.Variable(initializer([n_hidden1, n_hidden2]), name="W2")
b2 = tf.Variable(tf.zeros([n_hidden2,]), name="b2")
W3 = tf.transpose(W2, name="W3")
b3 = tf.Variable(tf.zeros([n_hidden1,]), name="b3")
W4 = tf.transpose(W1, name="W4")
b4 = tf.Variable(tf.zeros([n_inputs,]), name="b4")

# 构建模型
h1 = tf.nn.sigmoid(tf.nn.xw_plus_b(X, W1, b1))
h2 = tf.nn.sigmoid(tf.nn.xw_plus_b(h1, W2, b2))
h3 = tf.nn.sigmoid(tf.nn.xw_plus_b(h2, W3, b3))
outputs = tf.nn.sigmoid(tf.nn.xw_plus_b(h3, W4, b4))

# 定义loss
loss = -tf.reduce_mean(tf.reduce_sum(X * tf.log(outputs) +
                    (1 - X) * tf.log(1 - outputs), axis=1))
train_op = tf.train.AdamOptimizer(1e-02).minimize(loss)

当训练这个模型后，你可以将原始MNIST的数字手写体与重构出的手写体做个比较，如图3所示，上面是原始图片，而下面是重构图片，基本上没有差别了。尽管我们将维度从784降低到了150，得到的新特征还是抓取了原始特征的核心信息。

有一点，上面的训练过程是一下子训练完成的，其实对于堆栈编码器来说，有时候会采用逐层训练方式。直白点就是一层一层地训练：先训练X->h1的编码，使h1->X的重构误差最小化；之后再训练h1->h2的编码，使h2->h1的重构误差最小化。其实现代码如下：

# 构建模型
h1 = tf.nn.sigmoid(tf.nn.xw_plus_b(X, W1, b1))
h1_recon = tf.nn.sigmoid(tf.nn.xw_plus_b(h1, W4, b4))
h2 = tf.nn.sigmoid(tf.nn.xw_plus_b(h1, W2, b2))
h2_recon = tf.nn.sigmoid(tf.nn.xw_plus_b(h2, W3, b3))
outputs = tf.nn.sigmoid(tf.nn.xw_plus_b(h2_recon, W4, b4))

learning_rate = 1e-02
# X->h1
with tf.name_scope("layer1"):
    layer1_loss = -tf.reduce_mean(tf.reduce_sum(X * tf.log(h1_recon) +
                            (1-X) * tf.log(1-h1_recon), axis=1))
    layer1_train_op = tf.train.AdamOptimizer(learning_rate).minimize(layer1_loss,
                                            var_list=[W1, b1, b4])

# h1->h2
with tf.name_scope("layer2"):
    layer2_loss = -tf.reduce_mean(tf.reduce_sum(h1 * tf.log(h2_recon) +
                                    (1 - h1) * tf.log(1 - h2_recon), axis=1))
    layer2_train_op = tf.train.AdamOptimizer(learning_rate).minimize(layer2_loss,
                                                                 var_list=[W2, b2, b3])

分层训练之后，最终得到如图4所示的对比结果，结果还是不错的。

小结：

自动编码器应该是最通俗易懂的无监督神经网络模型，这里我们介绍了其基本原理及堆栈自动编码器。

参考文献：

1. Hands-On Machine Learning with Scikit-Learn and TensorFlow, Aurélien Géron, 2017.
2. Deep Learning Tutorials：Auto Encoders, Denoising Autoencoders.
3. Learning deep architectures for AI, Foundations and Trends in Machine Learning, Y. Bengio, 2009.