NNDL 作业11:优化算法比较
文章目录
-
- 1. 编程实现图6-1,并观察特征
- 2. 观察梯度方向
- 3. 编写代码实现算法,并可视化轨迹
- 4. 分析上图,说明原理(选做)
-
- 1.为什么SGD会走“之字形”?其它算法为什么会比较平滑?
- 2.Momentum、AdaGrad对SGD的改进体现在哪里?速度?方向?在图上有哪些体现?
- 3.仅从轨迹来看,Adam似乎不如AdaGrad效果好,是这样么?
- 5. 总结SGD、Momentum、AdaGrad、Adam的优缺点(选做)
- 6. Adam这么好,SGD是不是就用不到了?(选做)
- 总结
- 参考

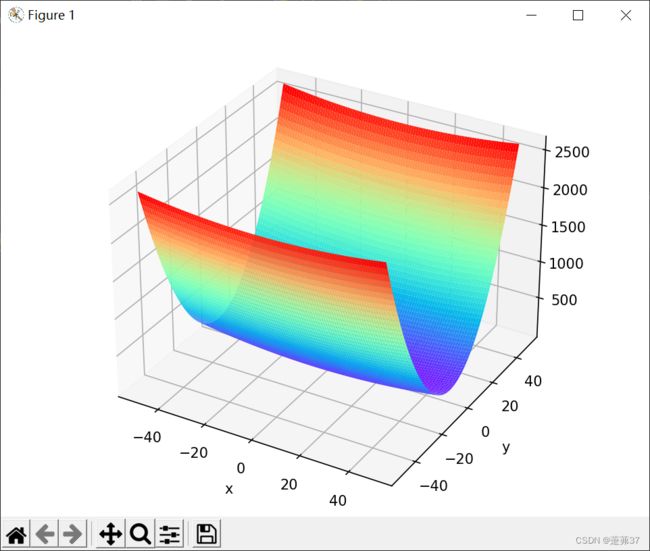
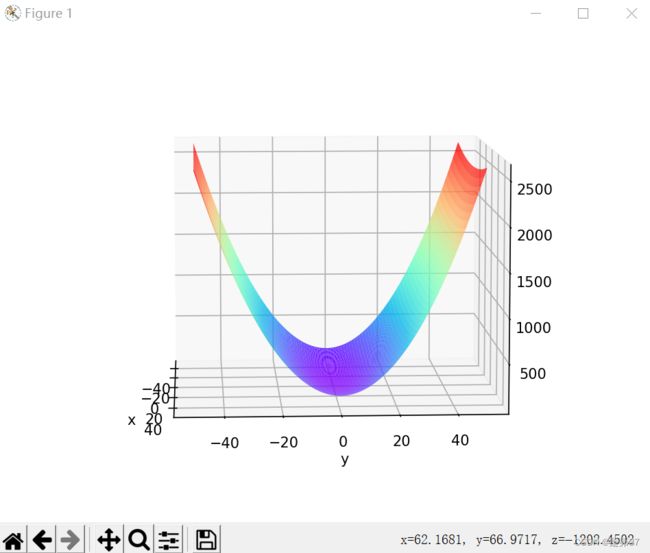
1. 编程实现图6-1,并观察特征
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x, y):
return x * x / 20 + y * y
def paint_loss_func():
x = np.linspace(-50, 50, 100) # x的绘制范围是-50到50,从改区间均匀取100个数
y = np.linspace(-50, 50, 100) # y的绘制范围是-50到50,从改区间均匀取100个数
X, Y = np.meshgrid(x, y)
Z = func(X, Y)
fig = plt.figure() # figsize=(10, 10))
ax = Axes3D(fig)
plt.xlabel('x')
plt.ylabel('y')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
paint_loss_func()
- 是向x轴方向延申的“碗”状函数,两端高,中间低。
- 等高线呈向x轴方向延申的椭圆状
- 有全局最小值
2. 观察梯度方向
 这个梯度的特征是,y轴方向上大,x轴方向上小。换句话说, 就是y轴方向的坡度大,而x轴方向的坡度小。这里需要注意的是,虽然式 (6.2)的最小值在(x, y)= (0, 0)处,但是图6-2中的梯度在很多地方并没有指向(0,0)。
这个梯度的特征是,y轴方向上大,x轴方向上小。换句话说, 就是y轴方向的坡度大,而x轴方向的坡度小。这里需要注意的是,虽然式 (6.2)的最小值在(x, y)= (0, 0)处,但是图6-2中的梯度在很多地方并没有指向(0,0)。
3. 编写代码实现算法,并可视化轨迹
代码如下:
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
class SGD:
"""随机梯度下降法(Stochastic Gradient Descent)"""
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
class Momentum:
"""Momentum SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
class Nesterov:
"""Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
def f(x, y):
return x ** 2 / 20.0 + y ** 2
def df(x, y):
return x / 10.0, 2.0 * y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z) # 绘制等高线
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.subplots_adjust(wspace=0, hspace=0) # 调整子图间距
plt.show()
4. 分析上图,说明原理(选做)
1.为什么SGD会走“之字形”?其它算法为什么会比较平滑?
- SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次,在样本量及其大的情况下,可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型,而且SGD没有动量的概念。
- 其他算法在下降开始阶段,历史速度变量和当前梯度方向相反,则会使得下降的过程更为平滑,避免过度震荡。因此主要作用在于:
有一定几率跳出局部最优解,历史速度变量和当前梯度方向相反时,使得下降的过程更为平滑。
2.Momentum、AdaGrad对SGD的改进体现在哪里?速度?方向?在图上有哪些体现?
-
Momentum

Momentum算法借用了物理中的动量概念,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力。
Momentum算法会观察历史梯度,若当前梯度的方向与历史梯度一致(表明当前样本不太可能为异常点),则会增强这个方向的梯度,若当前梯度与历史梯方向不一致,则梯度会衰减。 -
AdaGrad
 对于梯度大的参数设置小的步长,对于梯度小的参数,设置大的步长。类比于在缓坡上面,我们可以大步长的前进,在陡坡上面,这需要小步长的前进。adagrad则是参考了这个思路。上述的式子中,对梯度的平方进行了累加,所以r值一直都是递增的,故梯度的改变量会越来越小。对于较小的梯度,r的开方若小于1的,故梯度的改变量则较大,对于较大的梯度,r的开放较大,所以梯度改变量则较小。该优化方法的问题是,r的值一直是递增的,导致梯度梯度改变量会一直减小。也就是图中函数值趋向最小值的速度更快。
对于梯度大的参数设置小的步长,对于梯度小的参数,设置大的步长。类比于在缓坡上面,我们可以大步长的前进,在陡坡上面,这需要小步长的前进。adagrad则是参考了这个思路。上述的式子中,对梯度的平方进行了累加,所以r值一直都是递增的,故梯度的改变量会越来越小。对于较小的梯度,r的开方若小于1的,故梯度的改变量则较大,对于较大的梯度,r的开放较大,所以梯度改变量则较小。该优化方法的问题是,r的值一直是递增的,导致梯度梯度改变量会一直减小。也就是图中函数值趋向最小值的速度更快。
3.仅从轨迹来看,Adam似乎不如AdaGrad效果好,是这样么?
是。对于AdaGrad,虽然在稀疏场景下表现的非常好,但由于 V t \sqrt{V_t} Vt
是单调递增的,就会使得实际学习率 α / V t α / \sqrt{V_t} α/Vt
递减至0,训练提前结束。
对于Adam避免二阶动量累积,导致训练过程提前结束。
5. 总结SGD、Momentum、AdaGrad、Adam的优缺点(选做)
- SGD
优点:训练收敛速度快,可以在线更新模型,有几率跳出局部最优达到更好的局部最优或者全局最优 。
缺点:选择合适的learning rate比较困难;容易收敛到局部最优,并且在某些情况下可能被困在鞍点。
- Momentum
优点:一方面可以加快收敛速度,另一方面可以提高精度(减少震荡,使模型收敛更稳定)。
缺点:需要人工设定学习率,需要有可靠的初始化参数。
- AdaGrad
优点:前期gt较小的时候,regularizer较大,能够放大梯度;后期gt较大的时候。regularizer较小,能够约束梯度 ,适合处理稀疏梯度 。
缺点:仍依赖于人工设置一个全局学习率,在这里插入图片描述设置过大的话,会使regularizer过于敏感,对梯度的调节太大。在训练的中后期,分母上梯度平方的累加将会越来越大,从而梯度趋近于0,使得训练提前结束。
- Adam
优点:结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点;对内存需求较小;为不同的参数计算不同的自适应学习率;也适用于大多非凸优化,适用于大数据集和高维空间。
缺点:可能不收敛;可能错过全局最优解。
6. Adam这么好,SGD是不是就用不到了?(选做)
不是。先来看SGD,SGD没有动量的概念,也就是说: m t = g t m_{t}=g_{t} mt=gt; V t = I 2 V_{t}=I^{2} Vt=I2,可以看到下降梯度就是最简单的 η t = α ⋅ g t \eta _{t}=\alpha \cdot g_{t} ηt=α⋅gt,SGD最大的缺点是下降速度慢,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点。
SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。
SGD的一阶动量: m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t m _{t}=\beta _{1}\cdot m_{t-1}+\left ( 1- \beta _{1}\right )\cdot g _{t} mt=β1⋅mt−1+(1−β1)⋅gt
加上AdaDelta的二阶动量: V t = β 2 ⋅ V t − 1 + ( 1 − β 2 ) ⋅ g t 2 V_{t}=\beta _{2}\cdot V_{t-1}+\left ( 1- \beta _{2}\right )\cdot g _{t}^{2} Vt=β2⋅Vt−1+(1−β2)⋅gt2
优化算法里最常见的两个超参数 就都在这里了,前者控制一阶动量,后者控制二阶动量。
但Adam并不能适应所有的场合,首先Adam可能不收敛,二阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的数据可能发生巨变,使得 V t V_{t} Vt 可能会时大时小,不是单调变化。这就可能在训练后期引起学习率的震荡,导致模型无法收敛;其次,使用Adam可能错过全局最优解,同样的一个优化问题,不同的优化算法可能会找到不同的答案,但自适应学习率的算法往往找到非常差的答案。
-
充分了解数据——如果模型是非常稀疏的,那么优先考虑自适应学习率的算法。
-
根据你的需求来选择——在模型设计实验过程中,要快速验证新模型的效果,可以先用Adam进行快速实验优化;在模型上线或者结果发布前,可以用精调的SGD进行模型的极致优化。
-
先用小数据集进行实验。有论文研究指出,随机梯度下降算法的收敛速度和数据集的大小的关系不大。因此可以先用一个具有代表性的小数据集进行实验,测试一下最好的优化算法,并通过参数搜索来寻找最优的训练参数。
-
考虑不同算法的组合。先用Adam进行快速下降,而后再换到SGD进行充分的调优。切换策略可以参考本文介绍的方法。
-
数据集一定要充分的打散(shuffle)。这样在使用自适应学习率算法的时候,可以避免某些特征集中出现,而导致的有时学习过度、有时学习不足,使得下降方向出现偏差的问题。
-
训练过程中持续监控训练数据和验证数据上的目标函数值以及精度或者AUC等指标的变化情况。对训练数据的监控是要保证模型进行了充分的训练——下降方向正确,且学习率足够高;对验证数据的监控是为了避免出现过拟合。
-
制定一个合适的学习率衰减策略。可以使用定期衰减策略,比如每过多少个epoch就衰减一次;或者利用精度或者AUC等性能指标来监控,当测试集上的指标不变或者下跌时,就降低学习率。
总结
课上听老师讲结合课下实验对几种优化算法的比较,对SGD、Momentum、AdaGrad、Adam这几种优化算法有了更深的理解。通过做选做题对比优缺点,也有了更深的认识。SGD最大的缺点是下降速度慢,而且可能会陷入局部最优,Adam结合了几种算法的优点,但泛化能力差,总的来说不如SGD。
参考
深度学习常用优化方法总结——SGD,Momentum,AdaGrad,RMSProp,Adam
优化方法总结:SGD,Momentum,AdaGrad,RMSProp,Adam
Adam那么棒,为什么还对SGD念念不忘