机器学习笔记只隐马尔可夫模型(三)求值问题——前向算法(Forward Algorithm)
机器学习笔记之隐马尔可夫模型——前向算法处理求值问题
- 引言
-
- 回顾:隐马尔可夫模型
-
- 概念介绍
- 模型参数表示
- 隐马尔可夫模型的核心假设
- 关于 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)求解过程中的问题
- 前向算法
引言
上一节对隐马尔可夫模型(Hidden Markov Model,HMM)进行了归纳介绍。本节将详细介绍使用前向算法(Forward Algorithm)对处理求值(Evaluation)问题。
回顾:隐马尔可夫模型
隐马尔可夫模型是一个动态模型(Dynamic Model)。其主要特点是系统状态(System State)任意一个状态元素(隐变量),其取值范围是离散的。
以系统状态中 t t t时刻的状态元素 Z ( t ) \mathcal Z^{(t)} Z(t)为例,存在 K \mathcal K K个离散结果供 Z ( t ) \mathcal Z^{(t)} Z(t)进行选择。即:
Z ( t ) ∈ { z 1 , z 2 , ⋯ , z K } \mathcal Z^{(t)} \in \{z_1,z_2,\cdots,z_{\mathcal K}\} Z(t)∈{z1,z2,⋯,zK}
概念介绍
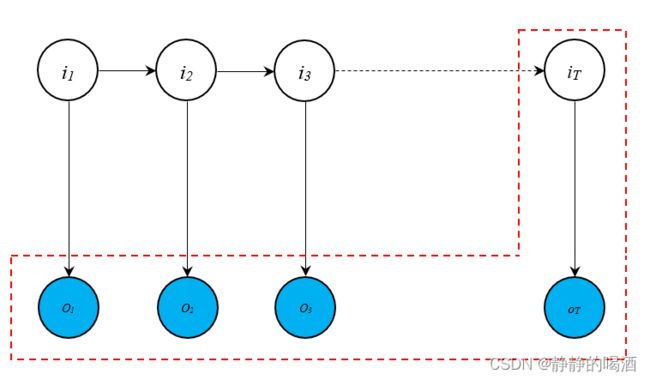
隐马尔可夫模型由状态序列与观测序列两部分构成:
I = { i 1 , i 2 , ⋯ , i t , i t + 1 , ⋯ , i T } O = { o 1 , o 2 , ⋯ , o t , o t + 1 , ⋯ , o T } \mathcal I = \{i_1,i_2,\cdots,i_t,i_{t+1},\cdots,i_T\} \\ \mathcal O = \{o_1,o_2,\cdots,o_t,o_{t+1},\cdots,o_T\} I={i1,i2,⋯,it,it+1,⋯,iT}O={o1,o2,⋯,ot,ot+1,⋯,oT}
其中状态序列中状态变量 i t ∈ I i_{t} \in \mathcal I it∈I的取值范围是离散的,并且状态变量可取到的状态值集合 Q \mathcal Q Q表示如下:
Q = { q 1 , q 2 , ⋯ , q K } \mathcal Q = \{q_1,q_2,\cdots,q_{\mathcal K}\} Q={q1,q2,⋯,qK}
观测序列中的观测变量 o t ∈ O o_t \in \mathcal O ot∈O的取值范围同样是离散的,并且观测变量可取到的观测值集合 V \mathcal V V表示如下:
V = { v 1 , v 2 , ⋯ , v M } \mathcal V = \{v_1,v_2,\cdots,v_\mathcal M\} V={v1,v2,⋯,vM}
模型参数表示
隐马尔可夫模型的模型参数 λ \lambda λ具体包含三项:
λ = ( π , A , B ) \lambda = (\pi,\mathcal A,\mathcal B) λ=(π,A,B)
- π \pi π称作 初始概率分布(基于状态变量),是一个 K \mathcal K K维向量。向量各元素表示初始状态变量 i 1 i_1 i1取到各离散结果 q 1 , q 2 , ⋯ , q K q_1,q_2,\cdots,q_{\mathcal K} q1,q2,⋯,qK 的概率值。即:
π = ( P ( i 1 = q 1 ) P ( i 1 = q 2 ) ⋮ P ( i 1 = q K ) ) K × 1 ∑ k = 1 K P ( i 1 = q k ) = 1 \pi = \begin{pmatrix}P(i_1 = q_1) \\ P(i_1 = q_2) \\ \vdots \\ P(i_1 = q_{\mathcal K})\end{pmatrix}_{\mathcal K \times 1} \sum_{k=1}^{\mathcal K} P(i_1 = q_k) = 1 π=⎝ ⎛P(i1=q1)P(i1=q2)⋮P(i1=qK)⎠ ⎞K×1k=1∑KP(i1=qk)=1 - A \mathcal A A称作状态转移矩阵。具体表示如下:
A = [ a i j ] K × K \mathcal A = [a_{ij}]_{\mathcal K \times \mathcal K} A=[aij]K×K
其中 a i j a_{ij} aij表示 t t t时刻下的状态变量 i t = q i i_t = q_i it=qi的条件下, t + 1 t+1 t+1时刻的状态变量 i t + 1 = q j i_{t+1}=q_j it+1=qj的概率。数学符号表示如下:
a i j = P ( i t + 1 = q j ∣ i t = q i ) i , j ∈ { 1 , 2 , ⋯ , K } a_{ij} = P(i_{t+1} = q_j \mid i_t = q_i) \quad i,j \in \{1,2,\cdots,\mathcal K\} aij=P(it+1=qj∣it=qi)i,j∈{1,2,⋯,K} - B \mathcal B B称作发射矩阵。具体表示如下:
B = [ b j ( k ) ] K × M \mathcal B = [b_j(k)]_{\mathcal K\times \mathcal M} B=[bj(k)]K×M
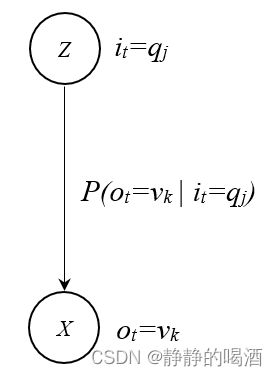
其中 b j ( k ) b_j(k) bj(k)表示 t t t时刻下状态变量 i t = q j i_t=q_j it=qj的条件下, t t t时刻下的观测变量 o t = v k o_t=v_k ot=vk的概率。数学符号表示如下:
b j ( k ) = P ( o t = v k ∣ i t = q j ) j ∈ { 1 , 2 , ⋯ , K } ; k ∈ { 1 , 2 , ⋯ , M } b_j(k) = P(o_t = v_k \mid i_t = q_j) \quad j \in \{1,2,\cdots,\mathcal K\};k \in \{1,2,\cdots,\mathcal M\} bj(k)=P(ot=vk∣it=qj)j∈{1,2,⋯,K};k∈{1,2,⋯,M}
隐马尔可夫模型的核心假设
- 齐次马尔可夫假设:
某时刻 t t t条件下,状态变量 i t i_t it的后验概率,只和前一时刻状态变量 i t − 1 i_{t-1} it−1相关,与其他变量无关;
数学符号表达如下:
P ( i t ∣ i t − 1 , ⋯ , i 1 , o t − 1 , o 1 ) = P ( i t ∣ i t − 1 ) P(i_{t} \mid i_{t-1},\cdots,i_1,o_{t-1},o_1) = P(i_t \mid i_{t-1}) P(it∣it−1,⋯,i1,ot−1,o1)=P(it∣it−1) - 观测独立性假设:
某时刻 t t t条件下,观测变量 o t o_t ot的后验概率,只和 t t t时刻的状态变量 i t i_t it相关,与其他变量无关。
数学符号表达如下:
P ( o t ∣ i t , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = P ( o t ∣ i t ) P(o_t \mid i_t,\cdots,i_1,o_{t-1},\cdots,o_1) = P(o_t \mid i_t) P(ot∣it,⋯,i1,ot−1,⋯,o1)=P(ot∣it)
关于 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)求解过程中的问题
求值问题描述:已知给定参数 λ \lambda λ的隐马尔可夫模型,求解观测序列 O = { o 1 , o 2 , ⋯ , o T } \mathcal O = \{o_1,o_2,\cdots,o_T\} O={o1,o2,⋯,oT}的后验概率结果 P ( O ∣ λ ) P(\mathcal O \mid \mathcal \lambda) P(O∣λ)。
或者可理解为’观测序列‘ O = { o 1 , o 2 , ⋯ , o T } \mathcal O = \{o_1,o_2,\cdots,o_T\} O={o1,o2,⋯,oT}通过HMM模型的计算所发生的概率。
首先,类似于高斯混合模型引入隐变量的方式,将将状态变量 I \mathcal I I引入到 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ):
因为'状态变量' I \mathcal I I的取值范围是离散的,因此积分方式是 ∑ \sum ∑;
P ( O ∣ λ ) = ∑ I P ( I , O ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) \begin{aligned} P(\mathcal O \mid \lambda) & = \sum_{\mathcal I} P(\mathcal I,\mathcal O \mid \lambda) \\ & = \sum_{\mathcal I} P(\mathcal O \mid \mathcal I,\lambda)P(\mathcal I \mid \lambda) \end{aligned} P(O∣λ)=I∑P(I,O∣λ)=I∑P(O∣I,λ)P(I∣λ)
- 观察 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ),它是关于状态变量 I \mathcal I I的概率分布。因此使用 状态转移矩阵 A \mathcal A A中的元素 进行表示:
- 将 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)展开成 P ( i 1 , i 2 , ⋯ , i T ∣ λ ) P(i_1,i_2,\cdots,i_{T}\mid \lambda) P(i1,i2,⋯,iT∣λ)的格式,并将其看作联合概率分布的形式,分解成条件概率的形式:
P ( I ∣ λ ) = P ( i 1 , i 2 , ⋯ , i T ∣ λ ) = P ( i T ∣ i 1 , i 2 , ⋯ , i T − 1 , λ ) ⋅ P ( i 1 , i 2 , ⋯ , i T − 1 ∣ λ ) \begin{aligned} P(\mathcal I \mid \lambda) & = P(i_1,i_2,\cdots,i_{T}\mid \lambda) \\ & = P(i_T \mid i_1,i_2,\cdots,i_{T-1},\lambda) \cdot P(i_1,i_2,\cdots,i_{T-1} \mid \lambda) \end{aligned} P(I∣λ)=P(i1,i2,⋯,iT∣λ)=P(iT∣i1,i2,⋯,iT−1,λ)⋅P(i1,i2,⋯,iT−1∣λ) - 观察上述公式的后项 P ( i 1 , i 2 , ⋯ , i T − 1 ∣ λ ) P(i_1,i_2,\cdots,i_{T-1} \mid \lambda) P(i1,i2,⋯,iT−1∣λ),它实际上就是个缩小版的 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ),和 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)相比,只少了一个 i T i_{T} iT项。因此,可以将 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)看成迭代式子。即:
P ( I ∣ λ ) = P ( i T ∣ i 1 , i 2 , ⋯ , i T − 1 , λ ) ⋅ P ( i 1 , i 2 , ⋯ , i T − 1 ∣ λ ) = P ( i T ∣ i 1 , i 2 , ⋯ , i T − 1 , λ ) ⋅ P ( i T − 1 ∣ i 1 , i 2 , ⋯ , i T − 2 , λ ) ⋅ P ( i 1 , i 2 , ⋯ , i T − 2 ∣ λ ) = ⋯ = P ( i T ∣ i 1 , i 2 , ⋯ , i T − 1 , λ ) ⋅ P ( i T − 1 ∣ i 1 , i 2 , ⋯ , i T − 2 , λ ) ⋯ P ( i 2 ∣ i 1 , λ ) ⋅ P ( i 1 ∣ λ ) \begin{aligned} P(\mathcal I \mid \lambda) & = P(i_T \mid i_1,i_2,\cdots,i_{T-1},\lambda) \cdot P(i_1,i_2,\cdots,i_{T-1} \mid \lambda) \\ & = P(i_T \mid i_1,i_2,\cdots,i_{T-1},\lambda) \cdot P(i_{T-1} \mid i_1,i_2,\cdots,i_{T-2},\lambda)\cdot P(i_1,i_2,\cdots,i_{T-2} \mid \lambda)\\ & = \cdots \\ & = P(i_T \mid i_1,i_2,\cdots,i_{T-1},\lambda) \cdot P(i_{T-1} \mid i_1,i_2,\cdots,i_{T-2},\lambda) \cdots P(i_2 \mid i_1,\lambda) \cdot P(i_1 \mid \lambda) \end{aligned} P(I∣λ)=P(iT∣i1,i2,⋯,iT−1,λ)⋅P(i1,i2,⋯,iT−1∣λ)=P(iT∣i1,i2,⋯,iT−1,λ)⋅P(iT−1∣i1,i2,⋯,iT−2,λ)⋅P(i1,i2,⋯,iT−2∣λ)=⋯=P(iT∣i1,i2,⋯,iT−1,λ)⋅P(iT−1∣i1,i2,⋯,iT−2,λ)⋯P(i2∣i1,λ)⋅P(i1∣λ) - 观察上式中的每一项,我们都可以使用 齐次马尔可夫假设 对每一项进行简化。例如: P ( i T ∣ i 1 , i 2 , ⋯ , i T − 1 , λ ) = P ( i T ∣ i T − 1 ) P(i_T \mid i_1,i_2,\cdots,i_{T-1},\lambda) = P(i_T \mid i_{T-1}) P(iT∣i1,i2,⋯,iT−1,λ)=P(iT∣iT−1),以此类推。
其中最后一项 P ( i 1 ∣ λ ) P(i_1 \mid \lambda) P(i1∣λ),即初始概率分布 π \pi π。最终 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)表示如下:
P ( I ∣ λ ) = P ( i T ∣ i T − 1 ) ⋅ P ( i T − 1 ∣ i T − 2 ) ⋯ P ( i 2 ∣ i 1 ) ⋅ π P(\mathcal I \mid \lambda) = P(i_T \mid i_{T-1}) \cdot P(i_{T-1} \mid i_{T-2}) \cdots P(i_2 \mid i_1) \cdot \pi P(I∣λ)=P(iT∣iT−1)⋅P(iT−1∣iT−2)⋯P(i2∣i1)⋅π - 观察状态转移过程图, P ( i T ∣ i T − 1 ) P(i_T \mid i_{T-1}) P(iT∣iT−1)使用 状态转移矩阵 A \mathcal A A中的元素进行表示:
P ( I ∣ λ ) = a i T − 1 , i T ⋅ a i T − 2 , i T − 1 ⋯ a i 1 , i 2 ⋅ π = π ⋅ ∏ t = 2 T a i t − 1 , i t \begin{aligned} P(\mathcal I \mid \lambda) & = a_{i_{T-1},i_{T}} \cdot a_{i_{T-2},i_{T-1}} \cdots a_{i_1,i_2} \cdot \pi \\ & = \pi \cdot \prod_{t=2}^{T}a_{i_{t-1},i_{t}} \end{aligned} P(I∣λ)=aiT−1,iT⋅aiT−2,iT−1⋯ai1,i2⋅π=π⋅t=2∏Tait−1,it
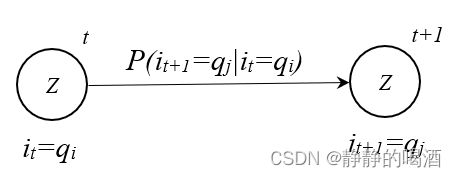
- 将 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)展开成 P ( i 1 , i 2 , ⋯ , i T ∣ λ ) P(i_1,i_2,\cdots,i_{T}\mid \lambda) P(i1,i2,⋯,iT∣λ)的格式,并将其看作联合概率分布的形式,分解成条件概率的形式:
- 继续观察 P ( O ∣ I , λ ) P(\mathcal O \mid \mathcal I,\lambda) P(O∣I,λ),和 P ( I ∣ λ ) P(\mathcal I \mid \lambda) P(I∣λ)相似,但依据的是 观测独立性假设。
- P ( O ∣ I , λ ) P(\mathcal O \mid \mathcal I,\lambda) P(O∣I,λ)中的 O , I \mathcal O,\mathcal I O,I进行展开,得到如下形式:
P ( O ∣ I , λ ) = P ( o 1 , ⋯ , o T ∣ i 1 , ⋯ , i T , λ ) = P ( o T ∣ o 1 , ⋯ , o T − 1 , i 1 , ⋯ , i T , λ ) ⋅ P ( o 1 , ⋯ , o T − 1 , i 1 , ⋯ , i T ∣ λ ) \begin{aligned} P(\mathcal O \mid \mathcal I ,\lambda) & = P(o_1,\cdots,o_T \mid i_1,\cdots,i_T,\lambda) \\ & = P(o_T \mid o_1,\cdots,o_{T-1},i_1,\cdots,i_{T},\lambda) \cdot P(o_1,\cdots,o_{T-1},i_1,\cdots,i_{T} \mid \lambda) \end{aligned} P(O∣I,λ)=P(o1,⋯,oT∣i1,⋯,iT,λ)=P(oT∣o1,⋯,oT−1,i1,⋯,iT,λ)⋅P(o1,⋯,oT−1,i1,⋯,iT∣λ) - 将上式展开成迭代形式:
P ( O ∣ I , λ ) = P ( o T ∣ o 1 , ⋯ , o T − 1 , i 1 , ⋯ , i T , λ ) ⋅ P ( o T − 1 ∣ o 1 , ⋯ , o T − 2 , i 1 , ⋯ , i T , λ ) ⋯ P ( o 1 ∣ i 1 , ⋯ i T , λ ) P(\mathcal O \mid \mathcal I ,\lambda) = P(o_T \mid o_1,\cdots,o_{T-1},i_1,\cdots,i_{T},\lambda) \cdot P(o_{T-1} \mid o_1,\cdots,o_{T-2},i_1,\cdots,i_{T},\lambda) \cdots P(o_1 \mid i_1,\cdots i_T,\lambda) P(O∣I,λ)=P(oT∣o1,⋯,oT−1,i1,⋯,iT,λ)⋅P(oT−1∣o1,⋯,oT−2,i1,⋯,iT,λ)⋯P(o1∣i1,⋯iT,λ) - 根据观测独立性假设,上述迭代形式表示如下:
P ( o T ∣ i T ) ⋅ P ( o T − 1 ∣ i T − 1 ) ⋯ P ( o 1 ∣ i 1 ) P(o_T \mid i_T) \cdot P(o_{T-1} \mid i_{T-1}) \cdots P(o_1 \mid i_1) P(oT∣iT)⋅P(oT−1∣iT−1)⋯P(o1∣i1) - 基于发射过程图, P ( o T ∣ i T ) P(o_T \mid i_T) P(oT∣iT)使用发射矩阵 B \mathcal B B结果进行表示:
P ( O ∣ I , λ ) = b i 1 ( o 1 ) ⋅ b i 2 ( o 2 ) ⋯ b i T ( o T ) = ∏ t = 1 T b i t ( o t ) \begin{aligned} P(\mathcal O \mid \mathcal I, \lambda) & = b_{i_1}(o_1) \cdot b_{i_2}(o_2) \cdots b_{i_T}(o_T) \\ & = \prod_{t=1}^T b_{i_t}(o_t) \end{aligned} P(O∣I,λ)=bi1(o1)⋅bi2(o2)⋯biT(oT)=t=1∏Tbit(ot)
- P ( O ∣ I , λ ) P(\mathcal O \mid \mathcal I,\lambda) P(O∣I,λ)中的 O , I \mathcal O,\mathcal I O,I进行展开,得到如下形式:
至此, P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)可以表示如下:
P ( O ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) = ∑ I π ⋅ ∏ t = 2 T a i t − 1 , i t ⋅ ∏ t = 1 T b i t ( o t ) \begin{aligned} P(\mathcal O \mid \lambda) & = \sum_{\mathcal I} P(\mathcal O \mid \mathcal I,\lambda)P(\mathcal I \mid \lambda) \\ & = \sum_{\mathcal I} \pi \cdot \prod_{t=2}^T a_{i_{t-1},i_{t}} \cdot\prod_{t=1}^T b_{i_t}(o_t) \end{aligned} P(O∣λ)=I∑P(O∣I,λ)P(I∣λ)=I∑π⋅t=2∏Tait−1,it⋅t=1∏Tbit(ot)
将上式中的 ∑ I \sum_{\mathcal I} ∑I部分展开,展开结果如下:
P ( O ∣ λ ) = ∑ i 1 ⋯ ∑ i T ( π ⋅ ∏ t = 2 T a i t − 1 , i t ⋅ ∏ t = 1 T b i t ( o t ) ) P(\mathcal O \mid \lambda) = \sum_{i_1} \cdots\sum_{i_T}\left(\pi \cdot \prod_{t=2}^T a_{i_{t-1},i_{t}} \cdot\prod_{t=1}^T b_{i_t}(o_t)\right) P(O∣λ)=i1∑⋯iT∑(π⋅t=2∏Tait−1,it⋅t=1∏Tbit(ot))
观察,大括号内的项均可以通过查找初始概率分布 π \pi π,状态转移矩阵 A \mathcal A A,发射矩阵 B \mathcal B B 得到。但括号外的 ∑ i 1 ⋯ ∑ i T \sum_{i_1} \cdots\sum_{i_T} ∑i1⋯∑iT中的每一项由于状态变量 i t ( t = 1 , 2 , ⋯ , T ) i_t(t=1,2,\cdots,T) it(t=1,2,⋯,T)均存在 K \mathcal K K种选择,因此上式的时间复杂度至少为 O ( K T ) O(\mathcal K^{T}) O(KT)。
即:状态序列 { i 1 , i 2 , ⋯ , i T } \{i_1,i_2,\cdots,i_T\} {i1,i2,⋯,iT}随着序列长度 T T T的增加,时间复杂度指数级别增长。下面将介绍关于求解 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)的优化算法——前向算法(Forward Algorithm)。
前向算法
- 我们记 α t ( i ) \alpha_t(i) αt(i)表示 在 t t t时刻,状态变量 i t = q i i_t = q_i it=qi的条件下, t t t时刻之前的所有观测变量(含 t t t时刻) o 1 , o 2 , ⋯ , o t o_1,o_2,\cdots,o_t o1,o2,⋯,ot与 i t i_t it的联合概率分布。数学符号表示如下:
α t ( i ) = P ( o 1 , ⋯ o t , i t = q i ∣ λ ) \alpha_t(i) = P(o_1,\cdots o_t,i_t = q_i \mid \lambda) αt(i)=P(o1,⋯ot,it=qi∣λ) - 基于上式, T T T时刻的 α T ( i ) \alpha_{T}(i) αT(i)表示如下:
即图中‘红色框’包含的变量。
α T ( i ) = P ( o 1 , ⋯ o T , i T = q i ∣ λ ) = P ( O , i T = q i ∣ λ ) \begin{aligned} \alpha_T(i) &= P(o_1,\cdots o_T,i_T = q_i \mid \lambda) \\ & =P(\mathcal O,i_T = q_i \mid \lambda) \end{aligned} αT(i)=P(o1,⋯oT,iT=qi∣λ)=P(O,iT=qi∣λ) - 如果求解 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ),只需求解 α T ( i ) \alpha_T(i) αT(i),然后将 i T i_T iT执行条件概率密度积分即可。数学符号表示如下:
同上,i T i_T iT自身存在K \mathcal K K种选择。
P ( O ∣ λ ) = ∑ i T P ( O , i T = q i ∣ λ ) = ∑ i = 1 K P ( O , i T = q i ∣ λ ) = ∑ i = 1 K α T ( i ) \begin{aligned} P(\mathcal O \mid \lambda) & = \sum_{i_T} P(\mathcal O,i_T = q_i \mid \lambda) \\ & = \sum_{i=1}^{\mathcal K} P(\mathcal O,i_T = q_i \mid \lambda) \\ & = \sum_{i=1}^{\mathcal K} \alpha_T(i) \end{aligned} P(O∣λ)=iT∑P(O,iT=qi∣λ)=i=1∑KP(O,iT=qi∣λ)=i=1∑KαT(i)
基于上述对 α t ( i ) \alpha_t(i) αt(i)的描述,我们尝试 观察 α t + 1 ( j ) \alpha_{t+1}(j) αt+1(j)和 α t ( i ) \alpha_t(i) αt(i)之间的关系。
- α t + 1 ( j ) \alpha_{t+1}(j) αt+1(j)具体表达如下:
α t + 1 ( j ) = P ( o 1 , ⋯ , o t , o t + 1 , i t + 1 = q j ∣ λ ) \alpha_{t+1}(j) = P(o_1,\cdots,o_t,o_{t+1},i_{t+1} = q_j \mid \lambda) αt+1(j)=P(o1,⋯,ot,ot+1,it+1=qj∣λ) - 但是上式中并不包含 i t i_t it项,因此,使用条件概率密度积分的方式将 i t i_t it加到公式中:
α t + 1 ( j ) = ∑ i t P ( o 1 , ⋯ , o t , o t + 1 , i t = q i , i t + 1 = q j ∣ λ ) = ∑ i = 1 K P ( o 1 , ⋯ , o t , o t + 1 , i t = q i , i t + 1 = q j ∣ λ ) \begin{aligned} \alpha_{t+1}(j) & = \sum_{i_t} P(o_1,\cdots,o_t,o_{t+1},i_t = q_i,i_{t+1} = q_j \mid \lambda) \\ & = \sum_{i=1}^{\mathcal K} P(o_1,\cdots,o_t,o_{t+1},i_t = q_i,i_{t+1} = q_j \mid \lambda) \end{aligned} αt+1(j)=it∑P(o1,⋯,ot,ot+1,it=qi,it+1=qj∣λ)=i=1∑KP(o1,⋯,ot,ot+1,it=qi,it+1=qj∣λ) - 但上述式子中仍包含 o t + 1 o_{t+1} ot+1项。因此,使用条件概率将上式分解,提出 o t + 1 o_{t+1} ot+1:
∑ i = 1 K [ P ( o t + 1 ∣ o 1 , ⋯ , o t , i t = q i , i t + 1 = q j , λ ) ⋅ P ( o 1 , ⋯ , o t , i t = q i , i t + 1 = q j ∣ λ ) ] \sum_{i=1}^{\mathcal K} \left[P(o_{t+1} \mid o_1,\cdots,o_t,i_t = q_i,i_{t+1} = q_j,\lambda) \cdot P(o_1,\cdots,o_t,i_t = q_i,i_{t+1} = q_j \mid \lambda)\right] i=1∑K[P(ot+1∣o1,⋯,ot,it=qi,it+1=qj,λ)⋅P(o1,⋯,ot,it=qi,it+1=qj∣λ)]
观察中括号内的第一项,可以使用观测独立性假设进行处理。并将上式改写如下形式:
∑ i = 1 K [ P ( o t + 1 ∣ i t + 1 = q j , λ ) ⋅ P ( o 1 , ⋯ , o t , i t = q i , i t + 1 = q j ∣ λ ) ] \sum_{i=1}^{\mathcal K} \left[P(o_{t+1} \mid i_{t+1}=q_j,\lambda) \cdot P(o_1,\cdots,o_t,i_t = q_i,i_{t+1} = q_j \mid \lambda)\right] i=1∑K[P(ot+1∣it+1=qj,λ)⋅P(o1,⋯,ot,it=qi,it+1=qj∣λ)] - 此时继续观察中括号内的后项: P ( o 1 , ⋯ , o t , i t = q i , i t + 1 = q j ∣ λ ) P(o_1,\cdots,o_t,i_t = q_i,i_{t+1} = q_j \mid \lambda) P(o1,⋯,ot,it=qi,it+1=qj∣λ),它和 α t ( i ) \alpha_t(i) αt(i)仅差一项: i t + 1 = q j i_{t+1} = q_j it+1=qj。
和 o t + 1 o_{t+1} ot+1项处理方式相同,继续使用条件概率将上式分解,提出 i t + 1 i_{t+1} it+1:
P ( o 1 , ⋯ , o t , i t = q i , i t + 1 = q j ∣ λ ) = P ( i t + 1 = q j ∣ o 1 , ⋯ , o t , i t = q i , λ ) ⋅ P ( o 1 , ⋯ , o t , i t = q i ∣ λ ) \begin{aligned} & P(o_1,\cdots,o_t,i_t = q_i,i_{t+1} = q_j \mid \lambda) \\ & = P(i_{t+1} = q_j \mid o_1,\cdots,o_t,i_t = q_i,\lambda) \cdot P(o_1,\cdots,o_t,i_t = q_i\mid \lambda) \end{aligned} P(o1,⋯,ot,it=qi,it+1=qj∣λ)=P(it+1=qj∣o1,⋯,ot,it=qi,λ)⋅P(o1,⋯,ot,it=qi∣λ)
观察上述式子第一项,可以使用齐次马尔科夫假设进行处理。并将上式改写成如下形式:
P ( i t + 1 = q j ∣ i t = q i , λ ) ⋅ P ( o 1 , ⋯ , o t , i t = q i ∣ λ ) = P ( i t + 1 = q j ∣ i t = q i , λ ) ⋅ α t ( i ) P(i_{t+1} = q_j \mid i_t = q_i,\lambda) \cdot P(o_1,\cdots,o_t,i_t = q_i\mid \lambda) = P(i_{t+1} = q_j \mid i_t = q_i,\lambda) \cdot \alpha_{t}(i) P(it+1=qj∣it=qi,λ)⋅P(o1,⋯,ot,it=qi∣λ)=P(it+1=qj∣it=qi,λ)⋅αt(i)
至此,整理 α t + 1 ( j ) \alpha_{t+1}(j) αt+1(j)和 α t ( i ) \alpha_{t}(i) αt(i)之间的关联关系:
α t + 1 ( j ) = ∑ i = 1 K [ P ( o t + 1 ∣ i t + 1 = q j ) ⋅ P ( i t + 1 = q j ∣ i t = q i , λ ) ⋅ α t ( i ) ] \alpha_{t+1}(j) = \sum_{i=1}^{\mathcal K} \left[P(o_{t+1} \mid i_{t+1}=q_j) \cdot P(i_{t+1} = q_j \mid i_t = q_i,\lambda) \cdot \alpha_{t}(i)\right] αt+1(j)=i=1∑K[P(ot+1∣it+1=qj)⋅P(it+1=qj∣it=qi,λ)⋅αt(i)]
如果使用模型参数进行表示:
α t + 1 ( j ) = ∑ i = 1 K b j ( o t + 1 ) ⋅ a i j ⋅ α t ( i ) \alpha_{t+1}(j) = \sum_{i=1}^{\mathcal K}b_j(o_{t+1}) \cdot a_{ij} \cdot \alpha_{t}(i) αt+1(j)=i=1∑Kbj(ot+1)⋅aij⋅αt(i)
最后观察它的时间复杂度:每次迭代的时间复杂度是 O ( N ) O(N) O(N),迭代 T T T次的时间复杂度即 O ( K × T ) O(\mathcal K \times T) O(K×T)。
而上述时间复杂度 描述的是 α 1 ( i ) → α T ( i ) \alpha_1(i) \to \alpha_T(i) α1(i)→αT(i)的时间复杂度,而 P ( O ∣ λ ) = ∑ i = 1 K α T ( i ) P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} \alpha_{T}(i) P(O∣λ)=∑i=1KαT(i)。因此, P ( O ∣ λ ) P(\mathcal O\mid \lambda) P(O∣λ)的时间复杂度为: O ( K 2 × T ) O(\mathcal K^2 \times T) O(K2×T),相比于 O ( K T ) O(\mathcal K^{T}) O(KT)还是要优化一些的。
下一节将介绍: 使用后向算法处理 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)问题。
相关参考:
机器学习-隐马尔可夫模型3-Evaluation问题-前向算法