（人工智能）线性/非线性规划问题求解

一、问题描述

二、拉格朗日和KKT条件的最优化问题

1、等式约束的优化

2、不等式约束的优化

三、利用拉格朗日手工求解问题

四、利用拉格朗日编程求解问题

# 导入包
from sympy import *
# 设置变量
x,y,z,k = symbols('x,y,z,k')
a,b,c=symbols('a,b,c')
f = 8*x*y*z
g = x**2/a**2+y**2/b**2+z**2/c**2-1
#构造拉格朗日函数
L=f+k*g
#求导
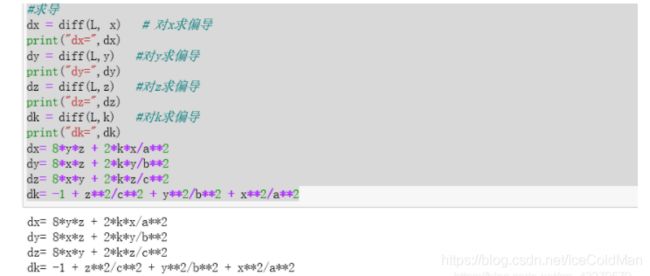
dx = diff(L, x)   # 对x求偏导
print("dx=",dx)
dy = diff(L,y)   #对y求偏导
print("dy=",dy)
dz = diff(L,z)   #对z求偏导
print("dz=",dz)
dk = diff(L,k)   #对k求偏导
print("dk=",dk)
dx= 8*y*z + 2*k*x/a**2
dy= 8*x*z + 2*k*y/b**2
dz= 8*x*y + 2*k*z/c**2
dk= -1 + z**2/c**2 + y**2/b**2 + x**2/a**2
#求出个变量解
m= solve([dx,dy,dz,dk],[x,y,z,k])   
print(m)
#变量赋值
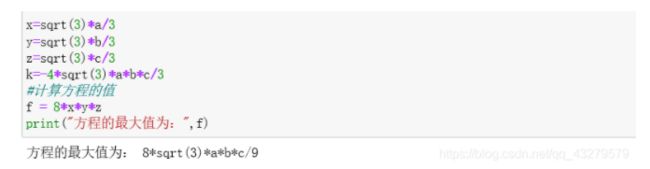
x=sqrt(3)*a/3
y=sqrt(3)*b/3
z=sqrt(3)*c/3
k=-4*sqrt(3)*a*b*c/3
#计算方程的值
f = 8*x*y*z
print("方程的最大值为：",f)

通过diff函数求解的偏导结果

通过solve函数求解变量的结果（根据题目要求，可知变量的值应该为正数）

最终结果

五、实际问题描述——媒体组合案例

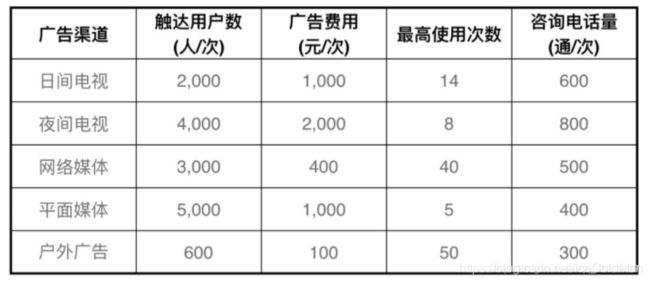
现有5个广告投放渠道，分别是日间电视、夜间电视、网络媒体、平面媒体、户外广告，每个渠道的效果、费用及限制如下表

其他限制条件
电视广告至少投放20次(包括日间和夜间)；
触达用户数(曝光量)不少于10万；
电视广告投入费用不超过3万元；
现在公司总共给到4万的营销费用，要求咨询电话量的最大化。

六、使用Excle实现线性规划

1、创建数据源
将下面数据输入表格

2、三要素

3、表格中设置目标函数

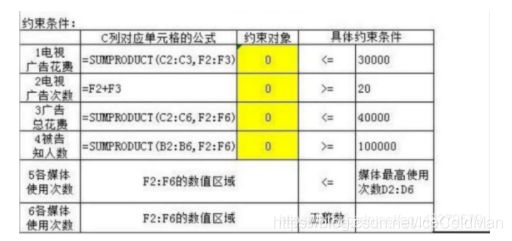
4、表格中设置约束条件

5、加载数据规划模块
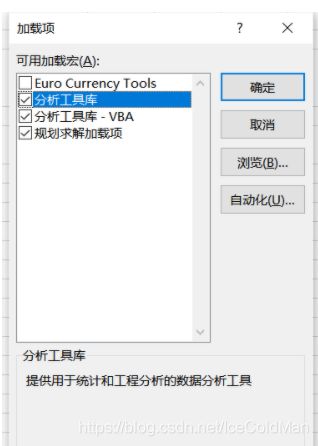
选择文件->更多->选项->加载项->转到，勾选上规划求解加载项

6、使用数据规划设置决策变量，目标函数和约束条件
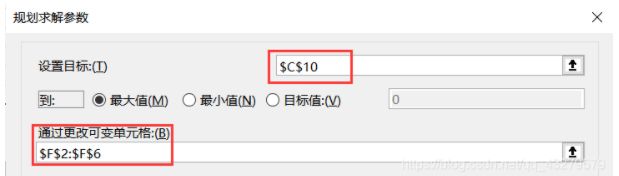
数据->规划求解
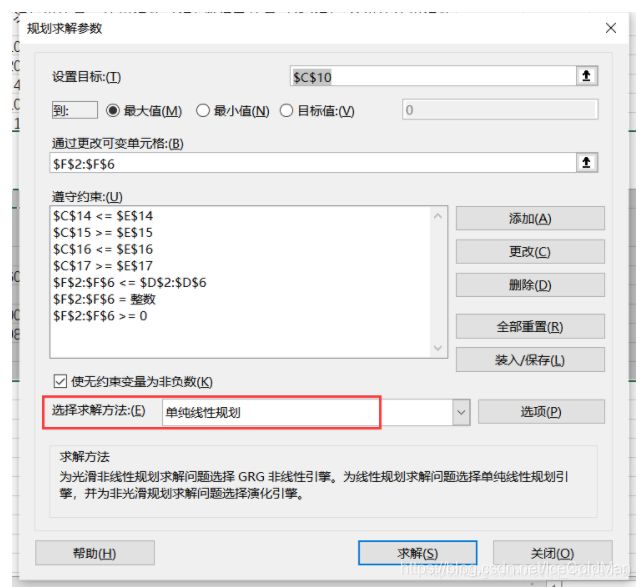
①设置目标函数和决策变量

②设置约束条件
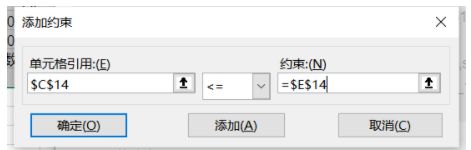
遵守约束->添加
约束条件1设置

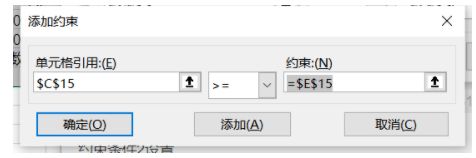
约束条件2设置

约束条件3设置

约束条件4设置

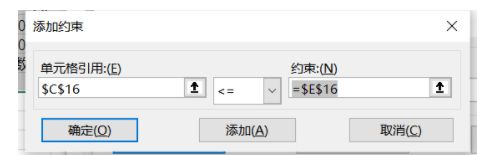
约束条件5设置

约束条件6设置

约束条件7设置

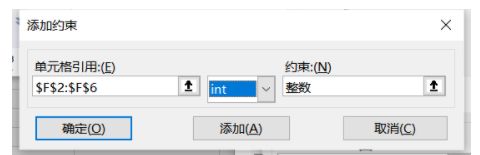
设置完成

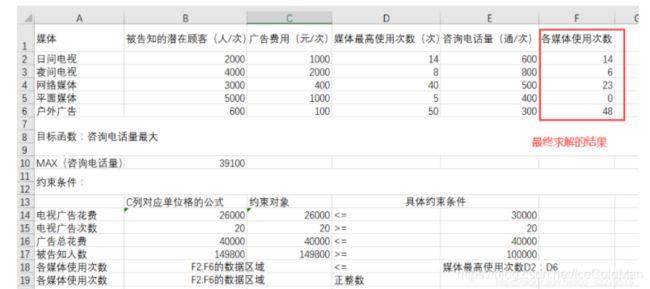
7、最终求解结果

七、使用Python编程实现线性规划

1、问题数学化

2、使用scipy库对线性规划的最优解、最大值进行求解

# 导入包
from scipy import optimize
import numpy as np
#创建矩阵，c为目标函数的矩阵，A_ub为约束条件的左边构成的矩阵，B_ub为约束条件的右边
c=np.array([600,800,500,400,300])
A_ub=np.array([[1000,2000,0,0,0],[-1,-1,0,0,0],[1000,2000,400,1000,100],[-2000,-4000,-3000,-5000,-600],[1,0,0,0,0],[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1]])
B_ub=np.array([30000,-20,40000,-100000,14,8,40,5,50])
# 求解
res=optimize.linprog(-c,A_ub,B_ub)
print(res)

3、求解结果

八、参考链接

https://blog.csdn.net/qq_43279579/article/details/115362675