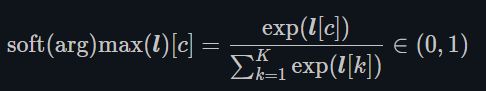第二次作业：深度学习基础

Assginment2：Basis of Deep Learning

本博客为OUC2022秋季软件工程第二周作业

一、问题

【第一部分】视频学习心得及问题总结

根据视频的学习内容，写一个总结，最后列出没有学明白的问题，针对大家的疑问，下次课会讨论一下，大家可提前把问题列出来。

【第二部分】代码练习

在谷歌 Colab 上完成 pytorch 代码练习中的 2.1 pytorch基础练习、2.2 螺旋数据分类，关键步骤截图，并附一些自己的想法和解读。

二、作业内容

ps：最后的实验体会有惊喜！

Part1 视频心得和问题总结

视频心得：

绪论部分：

机器学习并非最初用于有解析解的问题，而是用于给出一个近似解，但是随着问题复杂度的提升，后期也会有人采用使用机器学习解决存在解析解的问题。

参数模型：对数据分布做了假设

非参数模型：不对数据分布进行假设，数据的所有统计特性都来源于数据本身，且非参数模型的时空复杂度一般比参数模型大得多

AI方向在17年左右缺口较大，但是目前存在过热的趋势，且目前AI方向的应用并非很多，大致可行的落地项目分为cv和nlp两大类，在3，4年后这个行业是否会存在竞争压力过大而难以就业的问题

深度学习概述部分：

深度学习的概念起源于人工神经网络的研究，有多个隐层的多层感知器是深度学习模型的一个很好的范例。
深度学习的基本思想：假设有系统S，它有n层（S1，…，Sn），输入为I，输出为O，可形象的表示为：I=>S1=>S2=>… =>Sn=>O。为了使输出O尽可能的接近输入I，可以通过调整系统中的参数，这样就可以得到输入I的一系列层次特征S1，S2，…,Sn。对于堆叠的多个层，其中一层的输出作为其下一层的输入，以实现对输入数据的分级表达，这就是深度学习的基本思想。

深度神经网络是由多个单层非线性网络叠加而成的，常见的单层网络按照编码解码情况分为3类：只包含编码器部分、只包含解码器部分、既有编码器部分也有解码器部分。编码器提供从输入到隐含特征空间的自底向上的映射，解码器以重建结果尽可能接近原始输入为目标将隐含特征映射到输入空间。

1、 前馈深度网络

典型的前馈神经网络有多层感知机和卷积神经网络等。

(1) 单层卷积神经网络：

卷积阶段，通过提取信号的不同特征实现输入信号进行特定模式的观测。

(2) 卷积神经网络：

将单层的卷积神经网络进行多次堆叠，前一层的输出作为后一层的输入，便构成卷积神经网络。

(3) 卷积神经网络的特点：

卷积神经网络的特点在于，采用原始信号(一般为图像)直接作为网络的输入，避免了传统识别算法中复杂的特征提取和图像重建过程。

2、 反馈深度网络

典型的反馈深度网络有反卷积网络、层次稀疏编码网络等。

(1) 单层反卷积网络：

反卷积网络是通过先验学习，对信号进行稀疏分解和重构的正则化方法。

(2) 反卷积网络：

单层反卷积网络进行多层叠加，可得到反卷积网络。多层模型中，在学习滤波器组的同时进行特征图的推导，第L层的特征图和滤波器是由第L-1层的特征图通过反卷积计算分解获得。反卷积网络训练时，使用一组不同的信号y，求解C(y)，进行滤波器组f和特征图z的迭代交替优化。训练从第1层开始，采用贪心算法，逐层向上进行优化，各层间的优化是独立的。

(3) 反卷积网络的特点：

反卷积网络的特点在于，通过求解最优化输入信号分解问题计算特征，而不是利用编码器进行近似，这样能使隐层的特征更加精准，更有利于信号的分类或重建。

3、 双向深度网络

典型的双向深度网络有深度玻尔兹曼机、深度信念网络、栈式自编码器等。

(1) 受限玻尔兹曼机：

玻尔兹曼机(Boltzmann machine, BM)是一种随机的递归神经网络，由G. E.Hinton等提出，是能通过学习数据固有内在表示、解决复杂学习问题的最早的人工神经网络之一。

(2) 深度玻尔兹曼机：

将多个受限玻尔兹曼机堆叠，前一层的输出作为后一层的输入，便构成了深度玻尔兹曼机。

问题总结

1.有个讲了很久的东西，结果一个小时后你告诉我他过时了，有点仙人跳啊！

2.反卷积听得不是很明白

3.受限玻尔兹曼机有点疑问。

4.对梯度消失的理解

最底层的参数改变，传递到前面层的时候影响减小，被忽略。多层神经网络没办法传递，收敛情况没有单层神经网络好。梯度数学公式推导没有理解，存在一些问题。有什么其他方法解决梯度消失？梯度消失的解决在代码中应该怎么体现？

Part2 代码练习

感谢施雪雯同学贡献的代码和截图~
大家做的都很好，我就随便取了一个人的代码截图了。

2.1 pytorch 基础练习

凡是用Tensor进行各种运算的，都是Function

最终，还是需要用Tensor来进行计算的，计算无非是：

基本运算，加减乘除，求幂求余
布尔运算，大于小于，最大最小
线性运算，矩阵乘法，求模，求行列式
基本运算包括： abs/sqrt/div/exp/fmod/pow ，及一些三角函数 cos/ sin/ asin/ atan2/ cosh，及 ceil/round/floor/trunc

布尔运算包括： gt/lt/ge/le/eq/ne，topk, sort, max/min

线性计算包括： trace, diag, mm/bmm，t，dot/cross，inverse，svd 等

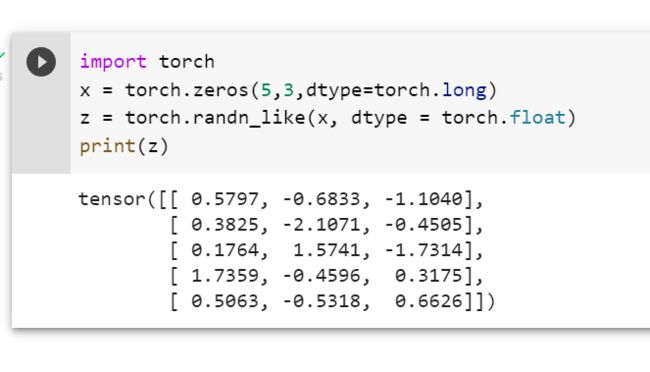
2.1.1. 定义数据

一般定义数据使用torch.tensor(), tensor的意思是张量,是数字各种形式的总称

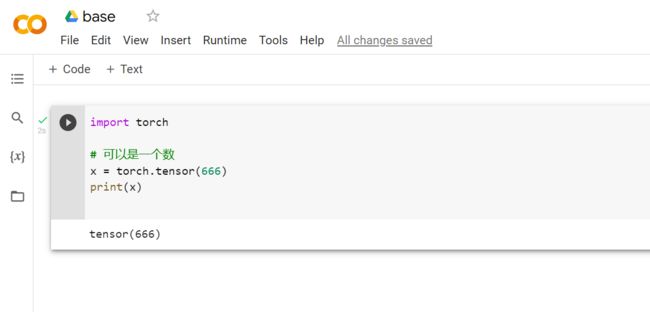
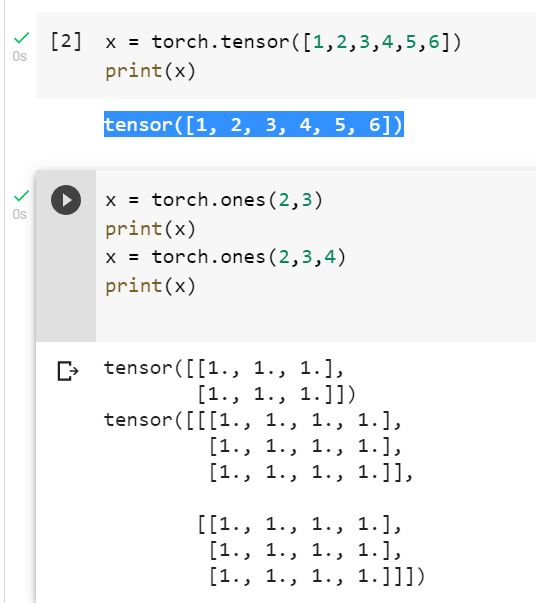
Tensor支持各种各样类型的数据，包括：
torch.float32, torch.float64, torch.float16, torch.uint8, torch.int8, torch.int16, torch.int32, torch.int64
创建Tensor有多种方法，包括：ones, zeros, eye, arange, linspace, rand, randn, normal, uniform, randperm

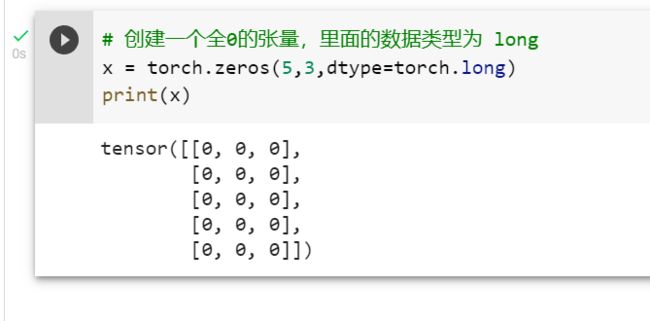
2.1.2. 定义操作

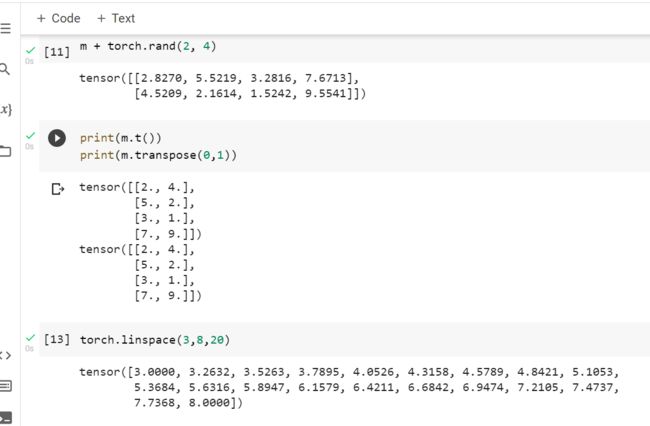
transpose()只能一次操作两个维度

函数返回输入矩阵input的转置

input (Tensor) – 输入张量，必填

dim0 (int) – 转置的第一维，默认0，可选

dim1 (int) – 转置的第二维，默认1，可选

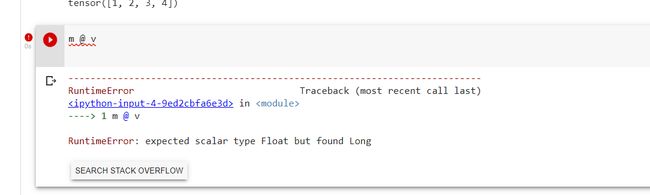
m @ v报错辽，这里的@符号表示两个矩阵的向量积，如N×W和W×C的两个矩阵相乘，得到结果为一个N×C的矩阵。需要注意，@和*还是不同的。*号表示两个矩阵对应元素直接相乘并非向量乘，如果形状不同可能会报错或者触发Python广播机制使得形状补齐相乘。

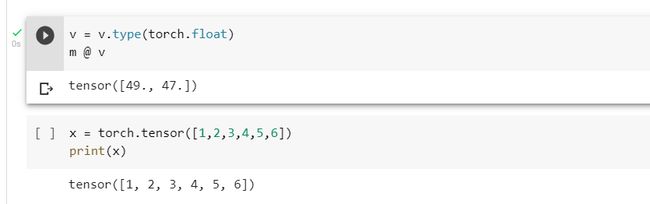
利用type修改元素类型后就可以成功运行了

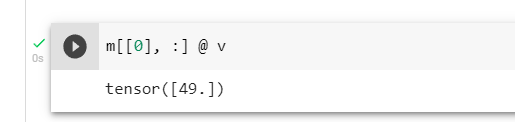
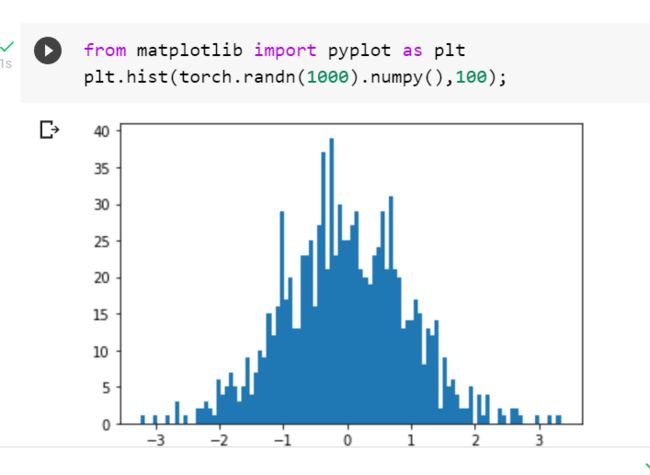
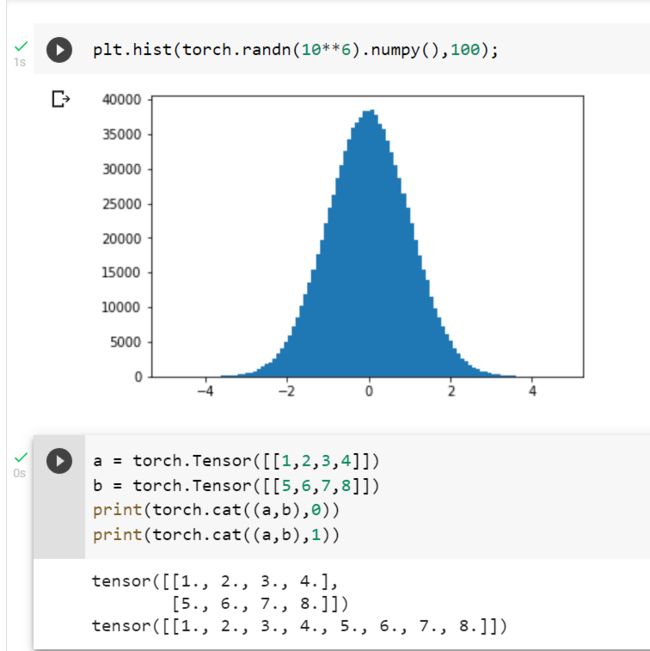
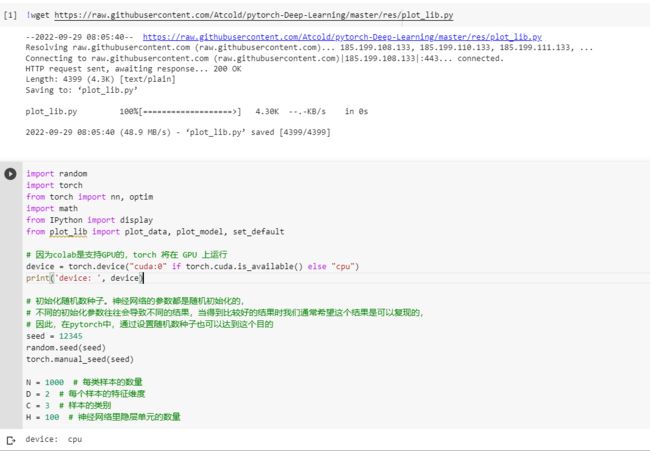
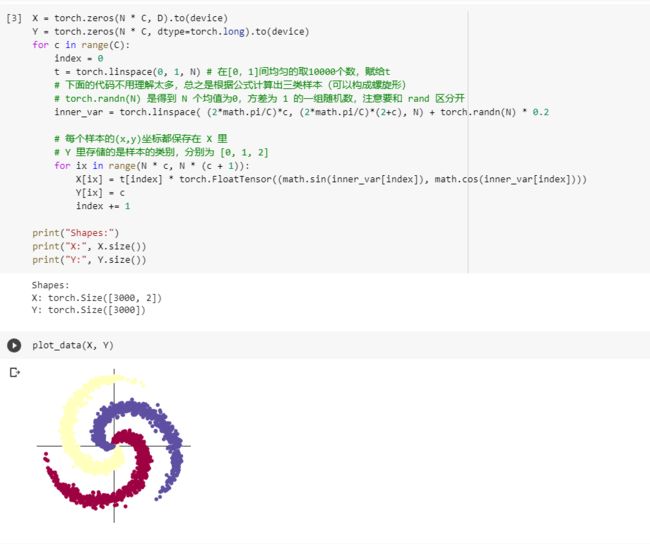
2.2 螺旋数据分类

2.2.1. 构建线性模型分类

optimizer手动将梯度清零可以减小内存消耗。

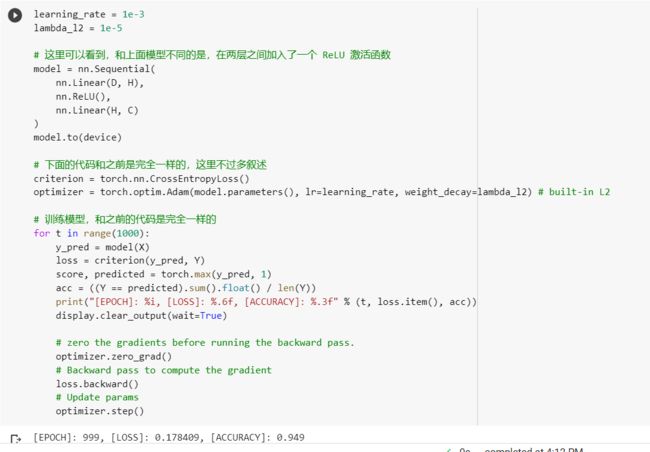
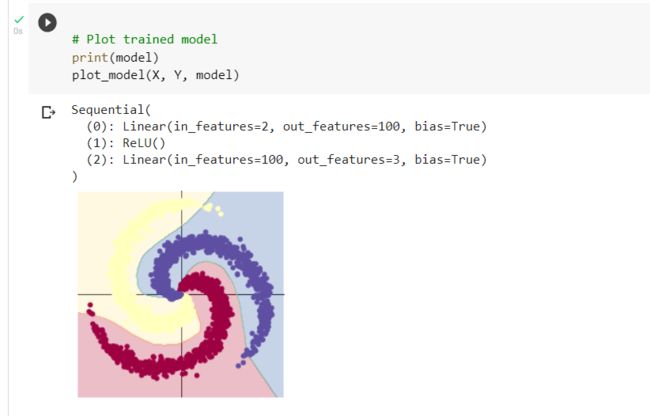
2.2.2. 构建两层神经网络分类

ReLU函数拥有单侧抑制，可以更好地挖掘相关特征，训练拟合数据。

实验体会

1.relu和sigmoid浅层对比

线性整流激活函数relu比sigmoid函数有更好的收敛效果。在三层网络之后，这个效果尤为明显，而sigmoid函数如果不进行数据预处理基本训练不动了。

仿照实验和视频，参考b站课程资料，写了一个简单的线性回归预测模型如下：

我这里是定义了四层网络。

import torch
import matplotlib.pyplot as plt
import numpy

#定义数据x，y
x = torch.unsqueeze(torch.linspace(-8,8,400),dim=1)
y = torch.sin(x)*0.7 + 0.3*torch.rand(x.size()) +2*torch.cos(x)*torch.rand(1)+x -0.05*x**2

#定义网络，构建网络
class Net(torch.nn.Module):
  def __init__(self,in_features,n_hidden_list,out_features):
    super(Net,self).__init__()
    #输入隐层列表来构建网络
    self.hidden =[]
    in_hidden = in_features
    for n_hidden in n_hidden_list:
      out_hidden = n_hidden
      self.hidden.append(torch.nn.Linear(in_hidden,out_hidden))
      in_hidden = n_hidden
    out_hidden = n_hidden_list[-1]
    self.predict = torch.nn.Linear(out_hidden,out_features)
  
  def forward(self,x):
    for hid in self.hidden:
      if(self.hidden.index(hid)==0):
        x=torch.sigmoid(hid(x))
      else:
        x=hid(x)
    x=self.predict(x)
    return x

#初始化网络
net = Net(1,[100,200,400],1)
lr = 0.001

#使用adam优化器
optimizer = torch.optim.Adam(net.parameters(),lr)
#使用均方差损失函数，也就是L2
loss_func = torch.nn.MSELoss()

epochs = 100000

plt.ion()

#开始训练
for epoch in range(epochs):
  #获取学习到的预测结果prediction
  prediction = net(x)
  #记录损失函数的损失
  loss = loss_func(prediction,y)
  #清空已经积累的梯度
  optimizer.zero_grad()
  #反向传播梯度
  loss.backward()
  #优化器根据梯度进行优化
  optimizer.step()
  if (epoch%10000 ==0):
    plt.cla()
    plt.scatter(x.data.numpy(),y.data.numpy())
    plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
    plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
    plt.pause(0.1)
plt.ioff()
plt.show()

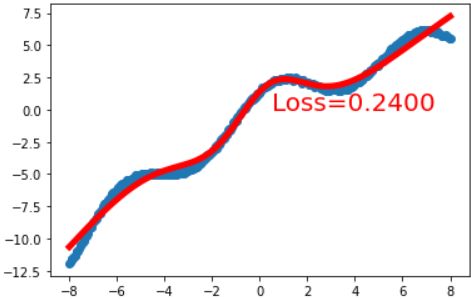
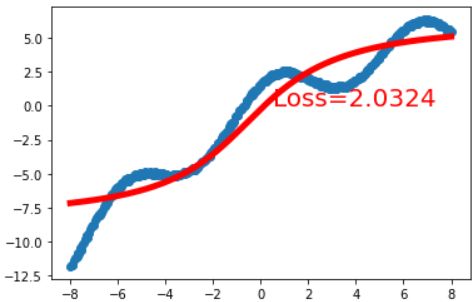
在此处我只给第一层加了sigmoid激活函数，设置epoch=5000轮，设置了初始学习率lr=0.01,优化器使用了Adam优化器,损失函数loss_func使用了均方差损失函数MSE。效果如下：

拟合的不算很好，不过还是能够训练的动的。但是如果每一个隐藏层都添加一个sigmoid激活函数呢？代码修改如下：

def forward(self,x):
    for hid in self.hidden:
      # if(self.hidden.index(hid)==0):
      #   x=torch.sigmoid(hid(x))
      # else:
      #   x=hid(x)
      x = torch.sigmoid(hid(x))
    x=self.predict(x)
    return x

拟合效果如下：

可见在训练轮数一定的情况下，他已经开始训练不动了，甚至可以说难以收敛
这也就是所谓梯度消失现象了。

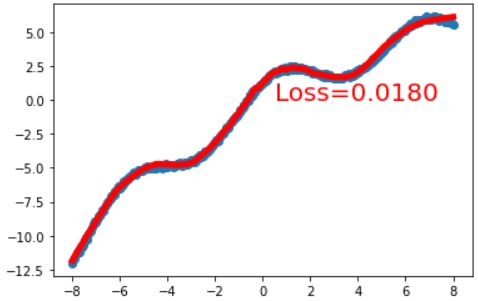
那如果每层都换成relu激活函数呢？

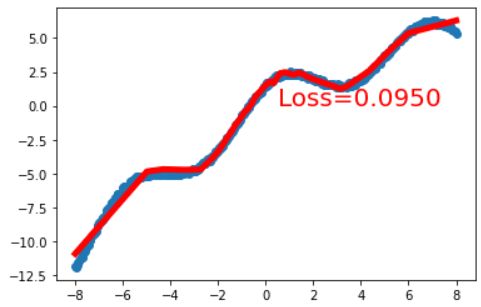
几乎完美拟合！同时我还观察到，训练的时间也比sigmoid短了很多！（图不放了）从这里我们可以看到如果采取多层relu函数，可以让线性分类变得更加平滑。这里可能还看不出来，下面我们只采用只有第一层用relu函数，就能看出区别了。

可以看到，在部分区间，这条拟合的趋向接近一条直线而非曲线！因为relu函数本身就是线性整流的，大于0的保留，而小于0的部分直接抑制。这也导致如果只用一层relu，分类的效果还是偏线性的。而多层relu函数可以解决此问题，使得拟合的模型更加容易非线性化。

2.线性模型分类

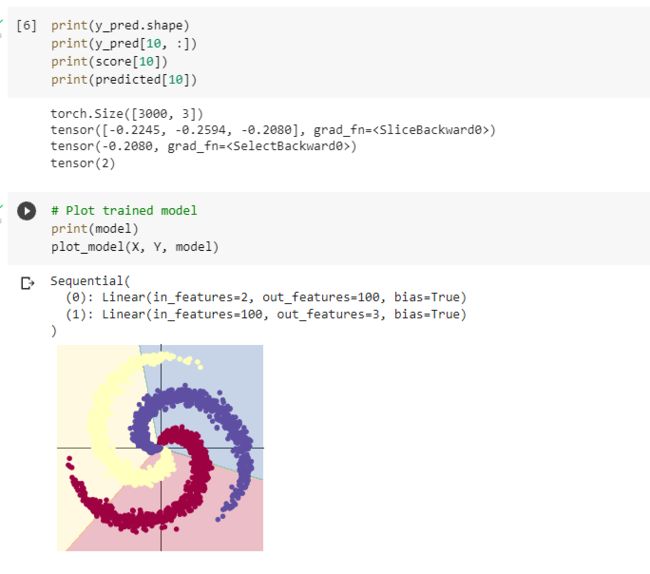
我略读了螺旋数据分类中，以下构建线性模型分类的代码

for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

当时有个疑问，就是求acc这一行代码，将Y标签类和预测类predicted比较的结果求和后为一个整数，整数/整数，在Python里面也能获得一个小数，为什么还需要添加float()函数，将前者强制转换为一个浮点数呢？

经过研究发下，原来Python3.0以下的版本，整数除整数只能得到一个整数,所以这里是为了兼容啊！（其实是自己没分清Python2和3的语法，不过值得一记）

然后逛博客看看大佬们都写了啥，偶然发现这么一个问题

我自己理解是，0+是这个预测的概率大于0，但无限接近于0;而1-,则是你预测概率出无限接近于1。至于为什么不是直接等于0和1，可以看下面我的解释。假设如果是完美的预测，他的损失函数就是几乎不损失吧，当然无限接近0最好啦！分析标签我们也可以知道，c=1的时候，y标签就是(1,0,0)，而y向量下标应该从1开始的。带入我们就知道损失函数l（yi，c）=-log（1-），这个损失函数就是0+了。对于不匹配的结果同理，-log（0+）=+∞！

关于为什么不可能等于0或者1，我是这么想的

看看下面这个公式，softmax函数。这个是将我们的分数转换为（0,1）区间上的一个函数，也就是把分数转换为概率的函数。

这里就解释了为什么预测的结果，y_hat（x）不可能是（1,0,0）了，因为使用这个后，你的概率肯定比0大，而你有三个类，分母都是指数，也一定比分子大，这也说明为什么不可能到1.