NNDL 实验六 卷积神经网络（1）卷积

目录

5.1 卷积

5.1.1 二维卷积运算

5.1.2 二维卷积算子

5.1.3 二维卷积的参数量和计算量

5.1.4 感受野

5.1.5 卷积的变种

5.1.6 带步长和零填充的二维卷积算子

5.1.7 使用卷积运算完成图像边缘检测任务

基于 Pytorch 实现的 Canny 边缘检测器

---

卷积神经网络（Convolutional Neural Network，CNN）

• 受生物学上感受野机制的启发而提出。
• 一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络
• 有三个结构上的特性：局部连接、权重共享、汇聚。
• 具有一定程度上的平移、缩放和旋转不变性。
• 和前馈神经网络相比，卷积神经网络的参数更少。
• 主要应用在图像和视频分析的任务上，其准确率一般也远远超出了其他的神经网络模型。
• 近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。

5.1 卷积

考虑到使用全连接前馈网络来处理图像时，会出现如下问题：

（1）模型参数过多，容易发生过拟合。 在全连接前馈网络中，隐藏层的每个神经元都要跟该层所有输入的神经元相连接。随着隐藏层神经元数量的增多，参数的规模也会急剧增加，导致整个神经网络的训练效率非常低，也很容易发生过拟合。

（2）难以提取图像中的局部不变性特征。 自然图像中的物体都具有局部不变性特征，比如尺度缩放、平移、旋转等操作不影响其语义信息。而全连接前馈网络很难提取这些局部不变性特征。

卷积神经网络有三个结构上的特性：局部连接、权重共享和汇聚。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。和前馈神经网络相比，卷积神经网络的参数也更少。因此，通常会使用卷积神经网络来处理图像信息。

卷积是分析数学中的一种重要运算，常用于信号处理或图像处理任务。本节以二维卷积为例来进行实践。

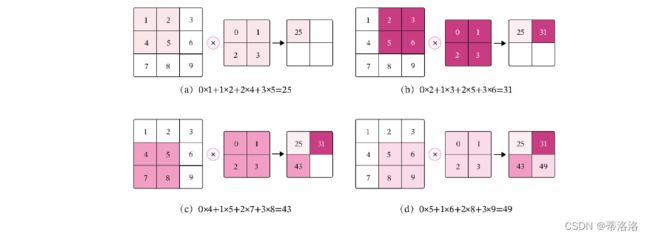
5.1.1 二维卷积运算

5.1.2 二维卷积算子

在本书后面的实现中，算子都继承paddle.nn.Layer，并使用支持反向传播的飞桨API进行实现，这样我们就可以不用手工写backword()的代码实现。

【使用pytorch实现】

import torch
import torch.nn as nn
import torch.nn
import numpy as np


class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        w = torch.tensor(np.array([[0., 1.], [2., 3.]], dtype='float32').reshape([kernel_size, kernel_size]))
        self.weight = torch.nn.Parameter(w, requires_grad=True)

    def forward(self, X):
        u, v = self.weight.shape
        output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])
        for i in range(output.shape[1]):
            for j in range(output.shape[2]):
                output[:, i, j] = torch.sum(X[:, i:i + u, j:j + v] * self.weight, axis=[1, 2])
        return output


# 随机构造一个二维输入矩阵
inputs = torch.as_tensor([[[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]])
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input: {}, \noutput: {}".format(inputs, outputs))

运行结果

 

5.1.3 二维卷积的参数量和计算量

随着隐藏层神经元数量的变多以及层数的加深，

使用全连接前馈网络处理图像数据时，参数量会急剧增加。

如果使用卷积进行图像处理，相较于全连接前馈网络，参数量少了非常多。

参数量

由于二维卷积的运算方式为在一个图像（或特征图）上滑动一个卷积核，通过卷积操作得到一组新的特征。所以参数量仅仅与卷积核的尺寸有关，对于一个输入矩阵和一个滤波器，卷积核的参数量为。

 假设有一幅大小为32×32的图像，如果使用全连接前馈网络进行处理，即便第一个隐藏层神经元个数为1，此时该层的参数量也高达1025个，此时该层的计算过程如下图所示。

 计算量

在卷积神经网络中运算时，通常会统计网络总的乘加运算次数作为计算量（FLOPs，floating point of operations），来衡量整个网络的运算速度。对于单个二维卷积，计算量的统计方式为：

 FLOPs=M′×N′×U×V。（5.4）

其中M′×N′表示输出特征图的尺寸，即输出特征图上每个点都要与卷积核进行U×V次乘加运算。对于一幅大小为32×32的图像，使用3×3的卷积核进行运算可以得到以下的输出特征图尺寸：

M′=M−U+1=30M′=M−U+1=30

N′=N−V+1=30N′=N−V+1=30

此时，计算量为：

 FLOPs=M′×N′×U×V=30×30×3×3=8100

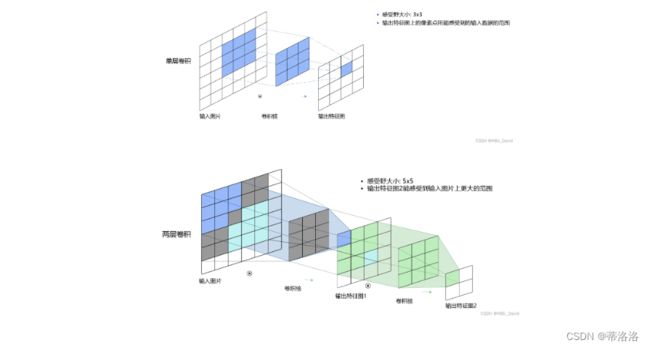
5.1.4 感受野

感受野就是特征图上的一个点对应输入图像上的区域。
它的英文名称是Receptive Field，我猜是可能要和人眼的视野对应上才叫的感受野，我觉得叫成 感受域也成。

它的定义是：The receptive field is defined as the size of the region in the input that produces the feature. 即 感受野的大小，等同于卷积核的大小；在feature map中，每个像素点的输入数据的选取，也是根据感受野的大小来取的；这个卷积核就像1个视野范围，把整张图从左到右，从上至下看了一遍。

当使用卷积遍历某个图片时，感受野过大或过小都是不合适的。

若目标相对感受野过小，那训练参数只有少部分是对应于训练目标的，则在测试环节，也很难检测出类似的目标；
若目标相对感受野过大，那训练的参数都是对应于整个对象的局部信息，是不够利于检测大小目标的。
所以对于感受野的大小选择，还是应当适当选取。

5.1.5 卷积的变种

5.1.5.1 步长（Stride）

在卷积运算的过程中，有时会希望跳过一些位置来降低计算的开销，也可以把这一过程看作是对标准卷积运算输出的下采样。

在计算卷积时，可以在所有维度上每间隔S个元素计算一次，S称为卷积运算的步长（Stride），也就是卷积核在滑动时的间隔。

此时，对于一个输入矩阵和一个滤波器，它们的卷积为

  

 在二维卷积运算中，当步长S=2时，计算过程如下图所示。 

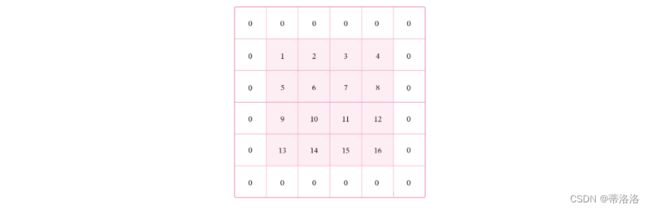
5.1.5.2 零填充（Zero Padding）

 对于一个输入矩阵和一个滤波器，，步长为S，对输入矩阵进行零填充，那么最终输出矩阵大小则为：

  

 引入步长和零填充后的卷积，参数量和计算量的统计方式与之前一致，参数量与卷积核的尺寸有关，为：U×V，计算量与输出特征图和卷积核的尺寸有关，为：

 

一般常用的卷积有以下三类： 

 1.窄卷积：步长S=1，两端不补零P=0，卷积后输出尺寸为：

M′=M−U+1,

N′=N−V+1.

2.宽卷积：步长S=1，两端补零P=U−1=V−1，卷积后输出尺寸为：

M′=M+U−1,

N′=N+V−1.

3.等宽卷积：步长S=1，两端补零，卷积后输出尺寸为：

M′=M,

N′=N.

通常情况下，在层数较深的卷积神经网络，比如：VGG、ResNet中，会使用等宽卷积保证输出特征图的大小不会随着层数的变深而快速缩减。例如：当卷积核的大小为3×3时，会将步长设置为S=1，两端补零P=1，此时，卷积后的输出尺寸就可以保持不变。在本章后续的案例中，会使用ResNet进行实验

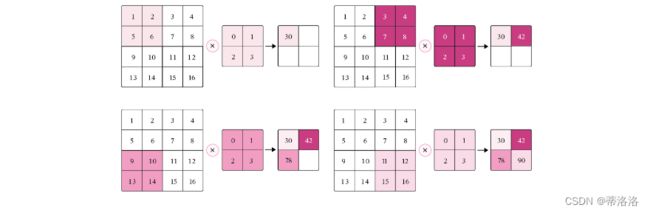
5.1.6 带步长和零填充的二维卷积算子

import torch
import torch.nn as nn
import torch.nn
import numpy as np


class Conv2D(nn.Module):
    def __init__(self, kernel_size,stride=1, padding=0):
        super(Conv2D, self).__init__()
        w = torch.tensor(np.array([[0., 1., 2.], [3., 4. ,5.],[6.,7.,8.]], dtype='float32').reshape([kernel_size, kernel_size]))
        self.weight = torch.nn.Parameter(w, requires_grad=True)
        self.stride = stride
        self.padding = padding

    def forward(self, X):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
        new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
        u, v = self.weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
                    axis=[1, 2])
        return output


inputs = torch.randn(size=[2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))

 

从输出结果看出，使用3×3大小卷积，

padding为1，

当stride=1时，模型的输出特征图与输入特征图保持一致；

当stride=2时，模型的输出特征图的宽和高都缩小一倍。

【使用pytorch实现】

5.1.7 使用卷积运算完成图像边缘检测任务

【使用pytorch实现】

 

import torch
import torch.nn as nn
import torch.nn
import numpy as np


class Conv2D(nn.Module):
    def __init__(self, kernel_size,stride=1, padding=0):
        super(Conv2D, self).__init__()
        # 设置卷积核参数
        w = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32').reshape((3,3))
        w=torch.from_numpy(w)
        self.weight = torch.nn.Parameter(w, requires_grad=True)
        self.stride = stride
        self.padding = padding

    def forward(self, X):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
        new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
        u, v = self.weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
                    axis=[1, 2])
        return output

import matplotlib.pyplot as plt
from PIL import Image
# 读取图片
img = Image.open('wuqimahei.jpg').convert('L')
img = np.array(img, dtype='float32')
im = torch.from_numpy(img.reshape((img.shape[0],img.shape[1])))

# 创建卷积算子，卷积核大小为3x3，并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2D(kernel_size=3, stride=1, padding=0)

# 将读入的图片转化为float32类型的numpy.ndarray
inputs = np.array(im).astype('float32')
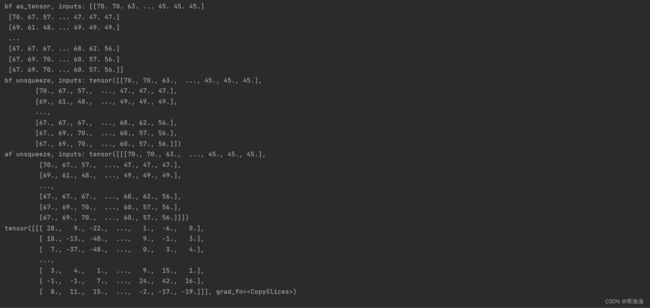
print("bf as_tensor, inputs:",inputs)
# 将图片转为Tensor
inputs = torch.as_tensor(inputs)
print("bf unsqueeze, inputs:",inputs)
inputs = torch.unsqueeze(inputs, axis=0)
print("af unsqueeze, inputs:",inputs)
outputs = conv(inputs)
print(outputs)
# outputs = outputs.data.squeeze().numpy()
# # 可视化结果
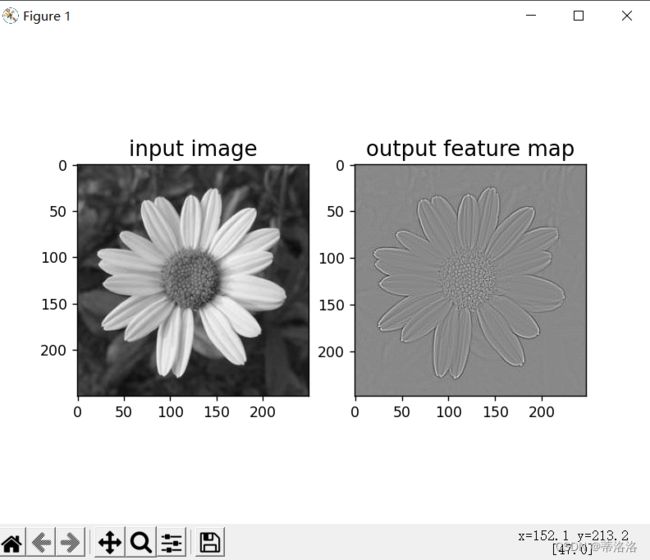
plt.subplot(121).set_title('input image', fontsize=15)
plt.imshow(img.astype('uint8'),cmap='gray')
plt.subplot(122).set_title('output feature map', fontsize=15)
plt.imshow(outputs.squeeze().detach().numpy(), cmap='gray')
plt.savefig('conv-vis.pdf')
plt.show()

 

实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian

基于 Pytorch 实现的 Canny 边缘检测器

import cv2
# 加载图像
image = cv2.imread('lu.png',0)
image = cv2.resize(image,(800,800))
def Canny(image,k,t1,t2):
    img = cv2.GaussianBlur(image, (k, k), 0)
    canny = cv2.Canny(img, t1, t2)
    return canny
image = cv2.resize(image, (800, 600))
cv2.imshow('Original Image', image)
output =cv2.resize(Canny(image,3,50,150),(800,600))
cv2.imshow('Canny Image', output)
# 停顿
if cv2.waitKey(0) & 0xFF == 27:
    cv2.destroyAllWindows()

 

 

 边缘检测系列3：【HED】 Holistically-Nested 边缘检测 - 飞桨AI Studio

 复现论文 Holistically-Nested Edge Detection，发表于 CVPR 2015 

一个基于深度学习的端到端边缘检测模型。

 

 边缘检测系列4：【RCF】基于更丰富的卷积特征的边缘检测 - 飞桨AI Studio (baidu.com)

 复现论文 Richer Convolutional Features for Edge Detection，CVPR 2017 发表

一个基于更丰富的卷积特征的边缘检测模型 【RCF】。

 

 边缘检测系列5：【CED】添加了反向细化路径的 HED 模型 - 飞桨AI Studio (baidu.com)

 Crisp Edge Detection（CED）模型是前面介绍过的 HED 模型的另一种改进模型

 

总结：

 这次作业让我受益很多，学到了很多，这次实验可以说是在加深印象，但是选做题上难度了，这里面好多都是在网上搜索参考荡下来的，后面的阅读也挺有意思，值得深入品读思考。

 参考文献：

(3条消息) NNDL 实验六 卷积神经网络（1）卷积_HBU_David的博客-CSDN博客