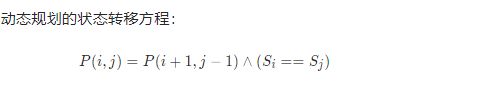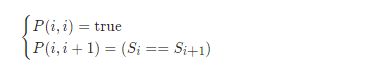【华为面试手撕代码】
文章目录
- 常用的排序算法
-
- 1.冒泡排序
- 2.选择排序
- 3.插入排序
- 4.快排排序
- 5.归并排序
- 6.堆排序
- Java 的sort基于什么实现
- 排序算法原理,何为稳定不稳定,快排是否稳定
- 查找
-
- 二分查找
- 复盘笔试题
-
- 3.寻找重复的子树
- 树的遍历方式
-
- 树的遍历方式(先序、中序、后序)
-
- 先序
- 中序
- 后序
- 如何用数组模拟二叉树的遍历过程?
- 求二叉树的深度两种方法
- 栈、队列
-
- 232. 用栈实现队列
- 225. 用队列实现栈
- 字符串
-
- 序列化与反序列化
- 统计字母出现次数从大到小排序
- 字符串中的最长不重复子串
- 动态规划
-
- 跳台阶
- 最长公共子序列
- 链表
-
- 反转链表
- leetcode 445. 两数相加 II
- 寻找字符串最长回文串
- 力扣14. 最长公共前缀
- 1701 平均等待时间
先说思路,然后写代码
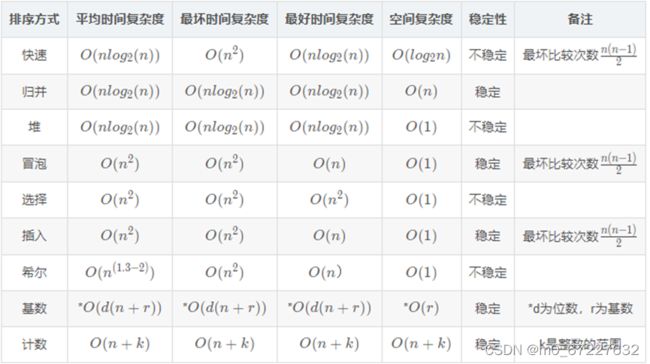
常用的排序算法
1.冒泡排序
1.设置循环次数。
2.设置开始比较的位数,和结束的位数。
3.两两比较,将最小的放到前面去。
重复2、3步,直到循环次数完毕。
int temp;//定义一个临时变量
for(int i=0;i<arr.length-1;i++){//冒泡趟数
for(int j=0;j<arr.length-i-1;j++){//从第一个比到n-1-i
if(arr[j+1]<arr[j]){//若前面比后面大,则交换
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
2.选择排序
1.首先在未排序序列中找到最小元素,存放到排序序列的起始位置。
2.再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
3.重复第二步,直到所有元素均排序完毕。
/* 选择排序 */
void SelectionSort(int arr[], int length)
{
int index, temp;
for (int i = 0; i < length; i++)
{
index = i;//未排序序列中最小元素
for (int j = i + 1; j < length; j++)
{
if (arr[j] < arr[index])
index = j;
}
if (index != i)
{
temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
}
}
3.插入排序
将数组R划分成两个子区间R[1..i-1](已排好序的有序区)和R[i..n](当前未排序的部分,可称无序区)。插入排序的基本操作是将当前无序区的第1个记录R[i]插人到有序区R[1..i-1]中适当的位置上,使R[1..i]变为新的有序区
public voidInsertSort () {
int i,j,temp;
for(i=1;i<array.length;i++) {// R[i..n](当前未排序的部分,可称无序区)
temp=array[i];
for(j=i-1;j>=0;j--) {// R[1..i-1](已排好序的有序区)
if(temp>array[j]) {
break;
}else {
array[j+1]=array[j];//往后挪,腾位置
}
}
array[j+1]=temp;//插入数据
}
}
4.快排排序
先从右往左找到一个小于基准数的数,再从左往右找到一个大于基准数的数,交换他们.重复,当ij相遇时把此时这个数和基准数交换,再分别处理左右两边的数字.
== 先从右往左找,再从左往右找==
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high) return;
i=low;
j=high;
temp = arr[low];//temp就是基准位
while (i<j) {
while (temp<=arr[j]&&i<j) {
j--;
}//先看右边,依次往左递减
while (temp>=arr[i]&&i<j) {
i++;
}//再看左边,依次往右递增
if (i<j) {//如果满足条件则交换
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
arr[low] = arr[i];//最后将基准为与i和j相等位置的数字交换
arr[i] = temp;
quickSort(arr, low, j-1);//递归调用左半数组
quickSort(arr, j+1, high);//递归调用右半数组
}
5.归并排序
假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到n/2个长度为2(或者是1)的有序子序列,再两两归并。如此重复,直到得到一个长度为n的有序序列为止。
private static void sort(int[] array, int left, int right) {
if (left == right) {
return;
}
int mid = left + ((right - left)/2);
sort(array, left, mid); // 对左侧子序列进行递归排序
sort(array, mid + 1, right); // 对右侧子序列进行递归排序
merge(array, left, mid, right); // 合并
}
private static void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = 0;
int p1 = left;
int p2 = mid + 1;
// 比较左右两部分的元素,哪个小,把那个元素填入temp中
while (p1 <= mid && p2 <= right) {
temp[i++] = array[p1] < array[p2] ? array[p1++] : array[p2++];
}
// 上面的循环退出后,把剩余元素依次填入temp(以下两个while只有一个会执行)
while (p1 <= mid) {
temp[i++] = array[p1++];
}
while (p2 <= right) {
temp[i++] = array[p2++];
}
// 把最终的排序的结果复制给原数组
for (i = 0; i < temp.length; i++) {
array[left + i] = temp[i];
}
}
6.堆排序
可以将堆看做是一个完全二叉树。并且,每个结点的值都大于等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于等于其左右孩子结点的值,称为小顶堆。
堆排序(Heap Sort)是利用堆进行排序的方法。其基本思想为:将待排序列构造成一个大顶堆(或小顶堆),整个序列的最大值(或最小值)就是堆顶的根结点,将根节点的值和堆数组的末尾元素交换,此时末尾元素就是最大值(或最小值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次大值(或次小值),如此反复执行,最终得到一个有序序列。
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
作者:尼小摩
链接:https://www.jianshu.com/p/a161b991fa82
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
public class HeapSort {
public static void main(String []args){
int []arr = {7,6,7,11,5,12,3,0,1};
System.out.println("排序前:"+Arrays.toString(arr));
sort(arr);
System.out.println("排序前:"+Arrays.toString(arr));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr,0,j);//重新对堆进行调整
}
}
//调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始
if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点
k++;
}
if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
Java 的sort基于什么实现
(快排),全都是快排吗(不知道)
排序算法原理,何为稳定不稳定,快排是否稳定
查找
二分查找
时间复杂度(logn)
复盘笔试题
笔试题的思路(说说上次笔试第二题为啥没全对??(答:估摸着边界没处理好)
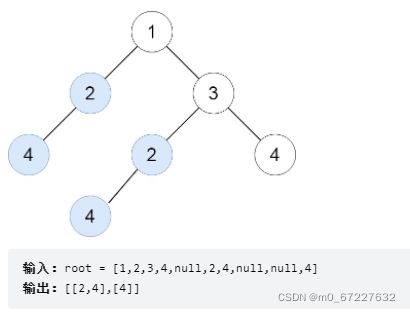
3.寻找重复的子树
题目:
给定一棵二叉树 root,返回所有重复的子树。
对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
如果两棵树具有相同的结构和相同的结点值,则它们是重复的
思路
序列化二叉树。
1
/ \
2 3
/ \
4 5
序列化结果为 1,2,#,#,3,4,#,#,5,#,#。每棵不同子树的序列化结果都是唯一的。
算法
使用深度优先搜索,其中递归函数返回当前子树的序列化结果。把每个节点开始的子树序列化结果保存在 mapmap 中,然后判断是否存在重复的子树。
class Solution {
Map<String, Integer> count;
List<TreeNode> ans;
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
count = new HashMap();
ans = new ArrayList();
collect(root);
return ans;
}
public String collect(TreeNode node) {
if (node == null) return "#";
String serial = node.val + "," + collect(node.left) + "," + collect(node.right);
count.put(serial, count.getOrDefault(serial, 0) + 1);
if (count.get(serial) == 2)
ans.add(node);
return serial;
}
}
树的遍历方式
树的遍历方式(先序、中序、后序)
先序
递归
// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
ArrayList<Integer> preOrderReverse(TreeNode root) {
ArrayList<Integer> result = new ArrayList<Integer>();
preOrder(root, result);
return result;
}
void preOrder(TreeNode root, ArrayList<Integer> result) {
if (root == null) {
return;
}
result.add(root.val); // 注意这一句
preOrder(root.left, result);
preOrder(root.right, result);
}
}
非递归
// 前序遍历顺序:中-左-右,入栈顺序:中-右-左
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null){
stack.push(node.right);
}
if (node.left != null){
stack.push(node.left);
}
}
return result;
}
}
中序
递归
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);
list.add(root.val); // 注意这一句
inorder(root.right, list);
}
}
非递归
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack=new Stack<>();
List<Integer> list=new ArrayList<>();
TreeNode cur=root;
while (cur!=null || !stack.isEmpty()){
while(cur!=null){
stack.push(cur);
cur=cur.left;
}
cur=stack.pop();
list.add(cur.val);
cur=cur.right;
}
return list;
}
}
后序
递归
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);
postorder(root.right, list);
list.add(root.val); // 注意这一句
}
}
非递归
// 后序遍历顺序 左-右-中 入栈顺序:中-左-右 出栈顺序:中-右-左, 最后翻转结果
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null){
stack.push(node.left);
}
if (node.right != null){
stack.push(node.right);
}
}
Collections.reverse(result);
return result;
}
}
如何用数组模拟二叉树的遍历过程?
顺序二叉树的满足条件:
1.一般指完全二叉树
2.第n个元素的左子树为2n+1;
3.第n个元素的右子树为2n+2;
4.第n个子树的父节点为(n-1)/2;
注意:n为数组下标所以是从0开始
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
//arrBinaryTree.preOrder(0);
//arrBinaryTree.infixOrder(0);
arrBinaryTree.postOrder(0);
}
}
class ArrBinaryTree {
private int[] arr;
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
//前序遍历数组
public void preOrder(int index) {
if (arr == null && arr.length == 0) {
System.out.println("数组为空");
return;
}
System.out.println(arr[index]);
if ((index * 2 + 1) < arr.length) {
preOrder(index * 2 + 1);
}
if ((index * 2 + 2) < arr.length) {
preOrder(index * 2 + 2);
}
}
//中序遍历
public void infixOrder(int index) {
if (arr == null && arr.length == 0) {
System.out.println("数组为空");
return;
}
//先遍历左子树 (index*2+1)
if ((index * 2 + 1) < arr.length) {
infixOrder(index * 2 + 1);
}
if (index < arr.length) {
System.out.print(arr[index] + "\t");
}
if ((index * 2 + 2) < arr.length) {
infixOrder(index * 2 + 2);
}
}
//后序遍历
public void postOrder(int index) {
if (arr == null && arr.length == 0) {
System.out.println("数组为空");
return;
}
if ((index * 2 + 1) < arr.length) {
postOrder(index * 2 + 1);
}
if ((index * 2 + 2) < arr.length) {
postOrder(index * 2 + 2);
}`在这里插入代码片`
if (index < arr.length) {
System.out.println(arr[index]+"\t");
}
}
}
求二叉树的深度两种方法
方法一:深度优先搜索
左子树和右子树的最大深度分别为 l 和 r,则二叉树的最大深度即为 max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此用「深度优先搜索」方法计算二叉树的最大深度。
在计算当前二叉树的最大深度时,先递归计算出其左子树和右子树的最大深度,然后在 O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}
}
方法二:广度优先搜索
广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候,每次只从队列里拿出一个节点,需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即一层一层地进行拓展,最后用一个变量ans 来维护拓展的次数,该二叉树的最大深度即为ans。
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
int ans = 0;
while (!queue.isEmpty()) {
int size = queue.size();
while (size > 0) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
size--;
}
ans++;
}
return ans;
}
}
栈、队列
232. 用栈实现队列
参考网址
入队(push)
一个队列是 FIFO 的,但一个栈是 LIFO 的。这就意味着最新压入的元素必须得放在栈底。为了实现这个目的,我们首先需要把 s1 中所有的元素移到 s2 中,接着把新元素压入 s2。最后把 s2 中所有的元素弹出,再把弹出的元素压入 s1。
出队(pop)
直接从 s1 弹出就可以了,因为 s1 的栈顶元素就是队列的队首元素。同时我们把弹出之后 s1 的栈顶元素赋值给代表队首元素的 front 变量。
判断空(empty)
s1 存储了队列所有的元素,所以只需要检查 s1 的是否为空就可以了。
取队首元素(peek)
在我们的算法中,用了 front 变量来存储队首元素,在每次 入队 操作或者 出队 操作之后这个变量都会随之更新。
private int front;
public void push(int x) {
if (s1.empty())
front = x;
while (!s1.isEmpty())
s2.push(s1.pop());
s2.push(x);
while (!s2.isEmpty())
s1.push(s2.pop());
}
public void pop() {
s1.pop();
if (!s1.empty())
front = s1.peek();
}
public boolean empty() {
return s1.isEmpty();
}
public int peek() {
return front;
}
入队(push)
新元素总是压入 s1 的栈顶,同时我们会把 s1 中压入的第一个元素赋值给作为队首元素的 front 变量。
出队(pop)
根据栈 LIFO 的特性,s1 中第一个压入的元素在栈底。为了弹出 s1 的栈底元素,我们得把 s1 中所有的元素全部弹出,再把它们压入到另一个栈 s2 中,这个操作会让元素的入栈顺序反转过来。通过这样的方式,s1 中栈底元素就变成了 s2 的栈顶元素,这样就可以直接从 s2 将它弹出了。一旦 s2 变空了,我们只需把 s1 中的元素再一次转移到 s2 就可以了。
判断空(empty)
s1 和 s2 都存有队列的元素,所以只需要检查 s1 和 s2 是否都为空就可以了。
取队首元素(peek)
我们定义了 front 变量来保存队首元素,每次 入队 操作我们都会随之更新这个变量。当 s2 为空,front 变量就是队首元素,当 s2 非空,s2 的栈顶元素就是队首元素。
private Stack<Integer> s1 = new Stack<>();
private Stack<Integer> s2 = new Stack<>();
public void push(int x) {
if (s1.empty())
front = x;
s1.push(x);
}
public void pop() {
if (s2.isEmpty()) {
while (!s1.isEmpty())
s2.push(s1.pop());
}
s2.pop();
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
public int peek() {
if (!s2.isEmpty()) {
return s2.peek();
}
return front;
}
225. 用队列实现栈
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中queue1用于存储栈内的元素,queue2作为入栈操作的辅助队列。
入栈操作
首先将元素入队到queue2,然后将queue1的全部元素依次出队并入队到queue2,此时queue 2的前端的元素即为新入栈的元素,再将queue1和queue2互换,则 queue1的元素即为栈内的元素,queue1 的前端和后端分别对应栈顶和栈底。
出栈操作
由于每次入栈操作都确保 queue1的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除queue1的前端元素并返回即可,
获得栈顶元素操作
只需要获得queue1的前端元素并返回即可(不移除元素)。
判断栈是否为空
由于queue1用于存储栈内的元素,判断栈是否为空时,只需要判断 queue1是否为空即可。
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<Integer>();
queue2 = new LinkedList<Integer>();
}
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty();
}
}
字符串
序列化与反序列化
题目:
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
思路: 先序遍历的递归思想
1.序列化:先序遍历结果(StringBuilder节约空间)
2.反序列化:将String类型转化为二叉树,
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder res=ser_help(root,new StringBuilder());
return res;
}
public StringBuilder res(TreeNode root,StringBuilder str){
if(root==null){
str.append("null,");
return str;
}
//先序遍历
str.append(root.val);
str.append(",");
str=ser_help(root.left,str);
str=ser_help(right.left,str);
return str;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] str_word = data.split(",");
List<String> list_word = new LinkedList<String>(Arrays.asList(str_word));
return deser_help(list_word);
}
public TreeNode deser_help(List<String> li){
if(li.get(0).equals("null")){
li.remove(0);
return null;
}
TreeNode res = new TreeNode(Integer.valueOf(li.get(0)));
li.remove(0);
res.left = deser_help(li);
res.right = deser_help(li);
return res;
}
}
统计字母出现次数从大到小排序
给出一个只包含字母的字符串,
不包含空格,统计字符串中各个子字母(区分大小写)出现的次数,
并按照字母出现次数从大到小的顺序输出各个字母及其出现次数
如果次数相同,按照自然顺序排序,且小写字母在大写字母之前
public class pr_73 {
public static void main(String[] args){
Scanner in=new Scanner(System.in);
String str=in.nextLine();
HashMap<Character,Integer> map=new HashMap<>();
for(int i=0;i<str.length();i++){
char c=str.charAt(i);
if(map.containsKey(c)) map.put(c, map.get(c)+1);
else map.put(c,1);
}
ArrayList<Map.Entry<Character,Integer>> list=new ArrayList<>();
list.addAll(map.entrySet());
Collections.sort(list, new Comparator<Map.Entry<Character, Integer>>() {
@Override
public int compare(Map.Entry<Character, Integer> o1, Map.Entry<Character, Integer> o2) {
if(o1.getValue()==o2.getValue())
return o1.getKey()-o2.getKey();
else return o2.getValue()-o1.getValue();
}
});
StringBuilder sb=new StringBuilder();
for(int i=0;i<list.size();i++){
sb.append(list.get(i).getKey()).append(":").append(list.get(i).getValue()).append(";");
}
String res= sb.toString();
System.out.print(res.substring(0,res.length()-1));
}
}
字符串中的最长不重复子串
「滑动窗口」
- 我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表枚举子串的起始位置,而右指针即为rk;
- 将左指针向右移动一格,表示开始枚举下一个字符作为起始位置,然后不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针开始的,不包含重复字符的最长子串。记录下这个子串的长度;
- 在枚举结束后,我们找到的最长的子串的长度即为答案。
class Solution {
public int lengthOfLongestSubstring(String s) {
// 哈希集合,记录每个字符是否出现过
Set<Character> occ = new HashSet<Character>();
int n = s.length();
// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
int rk = -1, ans = 0;
for (int i = 0; i < n; ++i) {
if (i != 0) {
// 左指针向右移动一格,移除一个字符
occ.remove(s.charAt(i - 1));
}
while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
// 不断地移动右指针
occ.add(s.charAt(rk + 1));
++rk;
}
// 第 i 到 rk 个字符是一个极长的无重复字符子串
ans = Math.max(ans, rk - i + 1);
}
return ans;
}
}
动态规划
跳台阶
public class pr_5_1 {
public static void main(String[] args){
Scanner in=new Scanner(System.in);
while (in.hasNext()){
int n= in.nextInt();
int res=find(n);
System.out.print(res);
}
}
public static int find(int n){//动态规划
int count=0;
if(n==1||n==2) return 1;
if(n==3) return 2;
if(n>3) count=find(n-1)+find(n-3);
return count;
}
}
public class pr_5 {
public static void main(String[] args){
Scanner in=new Scanner(System.in);
while (in.hasNext()){
int n= in.nextInt();
find(0,n);
System.out.print(count);
}
}
public static int count=0;
public static void find(int cur,int n){//递归
if(cur==n){
count++;
return ;
}
if(cur>n) return ;
find(cur+1,n);
find(cur+3,n);
}
}
最长公共子序列
(1) i == 0 || j == 0 LCS(i, j) = 0
(2) Xi ==Yj LCS(i, j) = LCS(i - 1,j- 1) + 1
(3) Xi !=Yj LCS(i, j) = max(LCS(i – 1, j) , LCS(i, j – 1))
public static int findLCS(String A, int n, String B, int m) {
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (A.charAt(i - 1) == B.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j] , dp[i][j - 1]);
}
}
}
return dp[n][m];
}
链表
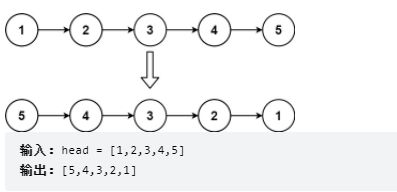
反转链表
题目:
给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。
方法一:迭代
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while (curr != null) {
ListNode next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
}
方法二:递归
递归版本稍微复杂一些,其关键在于反向工作。假设链表的其余部分已经被反转,现在应该如何反转它前面的部分?
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
leetcode 445. 两数相加 II
题目:
给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
思路与算法 : 栈
链表中数位的顺序与做加法的顺序是相反的,为了逆序处理所有数位,使用栈:把所有数字压入栈中,再依次取出相加。计算过程中需要注意进位的情况。
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
Deque<Integer> stack1 = new ArrayDeque<Integer>();
Deque<Integer> stack2 = new ArrayDeque<Integer>();
while (l1 != null) {
stack1.push(l1.val);
l1 = l1.next;
}
while (l2 != null) {
stack2.push(l2.val);
l2 = l2.next;
}
int carry = 0;
ListNode ans = null;
while (!stack1.isEmpty() || !stack2.isEmpty() || carry != 0) {
int a = stack1.isEmpty() ? 0 : stack1.pop();
int b = stack2.isEmpty() ? 0 : stack2.pop();
int cur = a + b + carry;
carry = cur / 10;
cur %= 10;
ListNode curnode = new ListNode(cur);
curnode.next = ans;
ans = curnode;
}
return ans;
}
}
寻找字符串最长回文串
思路:
动态规划的边界条件:
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
boolean[][] dp = new boolean[len][len];
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= len; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < len; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= len) {
break;
}
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
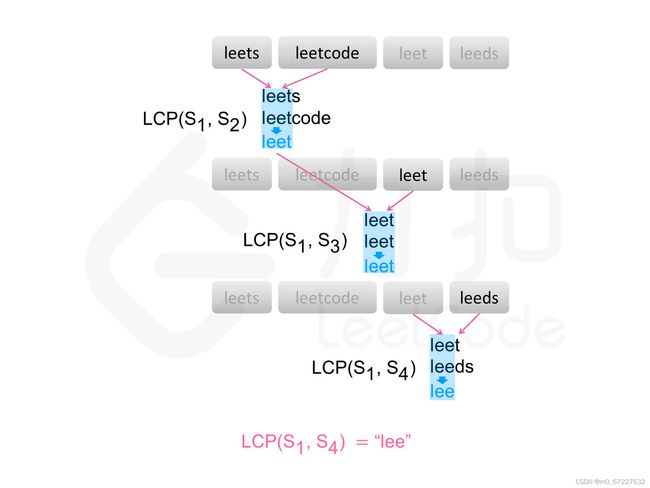
力扣14. 最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String prefix = strs[0];
int count = strs.length;
for (int i = 1; i < count; i++) {
prefix = longestCommonPrefix(prefix, strs[i]);
if (prefix.length() == 0) {
break;
}
}
return prefix;
}
public String longestCommonPrefix(String str1, String str2) {
int length = Math.min(str1.length(), str2.length());
int index = 0;
while (index < length && str1.charAt(index) == str2.charAt(index)) {
index++;
}
return str1.substring(0, index);
}
}
1701 平均等待时间
题目:
有一个餐厅,只有一位厨师。你有一个顾客数组 customers ,其中 customers[i] = [arrivali, timei] :
arrivali 是第 i 位顾客到达的时间,到达时间按 非递减 顺序排列。
timei 是给第 i 位顾客做菜需要的时间。
当一位顾客到达时,他将他的订单给厨师,厨师一旦空闲的时候就开始做这位顾客的菜。每位顾客会一直等待到厨师完成他的订单。厨师同时只能做一个人的订单。厨师会严格按照 订单给他的顺序 做菜。
请你返回所有顾客需要等待的 平均 时间。与标准答案误差在 10-5 范围以内,都视为正确结果。
示例 1:
输入:customers = [[1,2],[2,5],[4,3]]
输出:5.00000
解释:
1) 第一位顾客在时刻 1 到达,厨师拿到他的订单并在时刻 1 立马开始做菜,并在时刻 3 完成,第一位顾客等待时间为 3 - 1 = 2 。
2) 第二位顾客在时刻 2 到达,厨师在时刻 3 开始为他做菜,并在时刻 8 完成,第二位顾客等待时间为 8 - 2 = 6 。
3) 第三位顾客在时刻 4 到达,厨师在时刻 8 开始为他做菜,并在时刻 11 完成,第三位顾客等待时间为 11 - 4 = 7 。
平均等待时间为 (2 + 6 + 7) / 3 = 5 。
class Solution {
public double averageWaitingTime(int[][] customers) {
long endTime = 0;
long sum = 0;
for (int[] customer : customers) {
if (endTime <= customer[0]) {
endTime = customer[0];
}
endTime += customer[1];
sum += (endTime - customer[0]);
}
return sum * 1.0 / customers.length;
}
}