有趣的黑掉卫星Hack-A-Sat CTF比赛——模拟卫星视角beckley

以下内容是通过阅读《Hack-A-Sat太空信息安全挑战赛深度解题》做的测试。

题目介绍

Fire up your Google Earth and brush up on your KML tutorials, we're going to make it look at things!

题目描述得很简略，主办方希望参赛者利用Google Earth软件和KML文件寻找到设置的flag。给出的资料有：

（1）一个命名为static的文件夹，其中只有一个文件remote.kml，从后缀名可知，该文件是KML（Keyhole Markup Language，Keyhole标记语言）文件，KML是专门用于描述和保存地理信息的文件格式，其详细情况会在下文介绍。

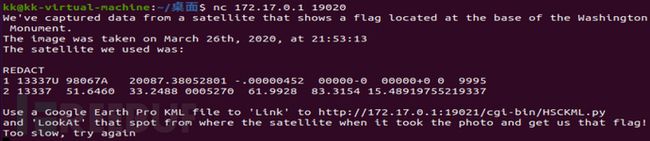
（2）给出了一个链接地址，使用nc连接到主办方给出的链接后，会得到进一步提示，如图2-1所示。

图2-1  beckley挑战题的提示信息

这段提示的内容就是告诉参赛者，当前截获了一颗卫星拍摄到的华盛顿纪念碑的照片，并且知道了这颗卫星的TLE（Two-Line Element，两行轨道根数）及照片的拍摄时间，要求参赛者在Google Earth中模拟卫星的拍摄角度、拍摄时间，就可以找到flag信息。

编译及测试

这道挑战题的代码位于beckley目录下，在该目录下打开终端，执行如下命令：

sudo make build

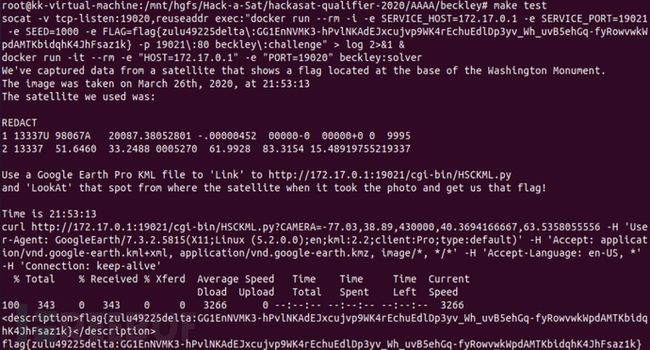
接着执行make test命令进行测试，输出如图2-2所示，可以发现测试中是使用curl工具访问Google Earth的，通过解析返回的信息，最终得到flag。

图2-2  beckley挑战题测试输出

为了更加清晰地显示解题过程，可以分开测试：

（1）打开一个终端，执行如下命令，其中端口号、flag值都可以随意设置，该命令的作用是运行一个beckley挑战题服务端容器。

socat -v tcp-listen:19020,reuseaddr exec:"docker run --rm -i -e SERVICE_HOST=172.17.0.1 -e SERVICE_PORT=19021 -e SEED=1000 -e FLAG=flag{zulu49225delta\:GG1EnNVMK3-hPvlNKAdEJxcujvp9WK

4rEchuEdlDp3yv_Wh_uvB5ehGq-fyRowvwkWpdAMTKbidqhK4JhFsaz1k} -p 19021\:80 beckley\:challenge"

（2）打开另一个终端，模拟参赛者，执行命令nc 172.17.0.1 19020，其中地址、端口就是第（1）步中启动服务端容器时设置的参数，其输出如图2-1所示，会给出题目进一步的提示。

（3）再打开一个终端，执行如下命令，该命令使用curl工具访问在第（2）步中提示的URL地址，其实是服务端容器模拟的Google Earth服务器地址。

curl http://172.17.0.1:19021/cgi-bin/HSCKML.py?CAMERA=-77.03,38.89,430000,40.3694166667,

63.5358055556-H 'User-Agent: GoogleEarth/7.3.2.5815(X11;Linux (5.2.0.0);en;kml:2.2;

client:Pro;type:default)' -H 'Accept: application/vnd.google-earth.kml+xml, application/

vnd.google-earth.kmz, image/*, */*' -H 'Accept-Language: en-US, *' -H 'Connection: keep-alive'

curl工具在URL地址后加入了很多参数，其中重要的是CAMERA参数，可以发现其由5个数字组成。在主办方提供的remote.kml文件中有如下描述，与curl工具使用的CAMERA参数很像，这是重点，具体含义会在下文分析中涉及到。

CAMERA=[lookatLon],[lookatLat],[lookatRange],[lookatTilt],[lookatHeading]

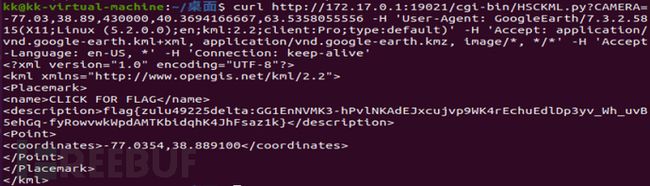
命令执行后，会返回KML格式的结果，如图2-3所示，从图中可以看出，在其中的标签的子标签内给出了flag信息。

图2-3  beckley挑战题获取到的flag

相关背景知识

1．卫星轨道和TLE轨道根数

太空中的卫星在地球引力等各种力的作用下做周期运动，一阶近似就是一个开普勒椭圆轨道。由于其他力的存在（如大气阻力、其他星球的引力等），实际的轨道和理想的开普勒轨道有偏离，称为“轨道摄动”。这里我们暂时不考虑摄动，只考虑理想开普勒轨道时的情况。

为了确定一个卫星的运行轨道，需要6个轨道参数，卫星运行轨道参数示意图示意图如图2-4所示。

（1）描述轨道大小的参数——轨道半长轴a。

轨道半长轴是椭圆长轴的一半。轨道半长轴与轨道周期具有对应关系，半长轴越大，轨道周期越长。

（2）描述轨道形状的参数——轨道偏心率e。

偏心率是指椭圆两焦点的距离与长轴的比值。偏心率为0时，轨道是圆；偏心率为0～1时，轨道是椭圆；偏心率为1时，轨道是抛物线；偏心率大于1时，轨道是双曲线。

图2-4  卫星运行轨道参数示意图

（3）描述轨道平面在空间方位的参数——轨道倾角i和升交点赤经Ω。

轨道倾角是指轨道平面和地球赤道平面的夹角。倾角小于90°时，为顺行轨道，卫星总是从西（西南或西北）向东（东北或东南）运行；倾角大于90°时，为逆行轨道，卫星的运行方向与顺行轨道相反；倾角为0°时，为赤道轨道；倾角为90°时，为极轨道。

升交点赤经是指轨道升交点和春分点对地心的张角。卫星从南半球运行到北半球时穿过赤道平面的那一点称为升交点。轨道倾角和升交点赤经共同决定轨道平面在空间的方位。

（4）描述轨道在轨道平面内方位的参数——近地点幅角ω。

近地点幅角是指近地点和升交点对地心的张角。轨道倾角和升交点赤经虽然决定了轨道平面在空间的位置，但是轨道本身在轨道平面中还可以转动，而这个值则确定了轨道在轨道平面中的位置。

（5）描述卫星在轨道上位置的参数——过近地点时刻τ。

过近地点时刻是指卫星经过近地点的时刻，它以年、月、日、时、分、秒表示。卫星位置随时间的变化需要一个初值，即运动时间起算点，可以利用开普勒方程计算出卫星在τ+t时刻的轨道位置和速度。

值得注意的是，上面的6个参数并不是唯一可以描述卫星轨道情况的参数，也可以选取其他参数，上面选取的这组参数是比较自然的一组。

TLE（Two-Line Element，两行轨道根数）用来记录卫星星历信息，覆盖了气象卫星、海洋卫星、地球资源卫星、教育卫星等应用卫星。其结构为3行，首行数据为卫星名称，后面两行存储了卫星相关数据，每行69个字符，包括0～9、A～Z（大写）、空格、点和正负号。

以北斗的某颗卫星的TLE数据为例，数据如下：

BEIDOU 2A

1 30323U 07003A     07067.68277059  .00069181  13771-5  44016-2 0  587

2 30323 025.0330 358.9828 7594216 197.8808 102.7839 01.92847527  650

第1行主要元素解析如下：

（1）30323U：30323是北美防空司令部给出的卫星编号。U表示不保密。我们看到的都是U，否则我们就不会看到这组TLE了。

（2）07003A：国际编号，07表示2007年；003表示这一年的第3次发射；A表示这次发射编号为A的物体，其他还有B、C、D等。国际编号就是2007-003A。

（3）07067.68277059：这组轨道数据的时间点，07表示2007年；067表示第67天，也就是3月8日；68277059表示这一天的时刻，大约是16时22分左右。

（4）.00069181  13771-5  44016-2：轨道模型参数，分别表示平均运动的一阶时间导数除2、平均运动的二阶时间导数除6（0.13771E-5）、BSTAR拖调制系数（0.44016E-2）。

（5）0：轨道模型，0表示采用SGP41SDP4轨道模型。

（6）58：表示这是关于这个空间物体的第58组TLE。

（7）7：最后一位是校验位。

第2行主要元素解析如下：

（1）30323：北美防空司令部给出的卫星编号。

（2）025.0330：轨道倾角。

（3）358.9828：升交点赤经。

（4）7594216：轨道偏心率，0.7594216，表示这是一个椭圆。

（5）197.8808：近地点幅角。

（6）102.7839：平近点角，表示这组TLE对应的时刻时，卫星在轨道的什么位置。它和参数过近地点时刻可以互相推导。

（7）01.92847527：每天环绕地球的圈数。它的倒数就是卫星运行的轨道周期。可以看出，这颗北斗卫星目前的周期大约是12h（0.5天）。周期和轨道半长轴有简单的换算关系，因此TLE的关于轨道的6要素和我们前面说的6要素是完全可以互相推导的。

（8）65：发射以来飞行的圈数。

（9）0：校验位。

2．KML文件格式

KML（Keyhole Markup Language，Keyhole标记语言）最初是由Google旗下的Keyhole公司开发和维护的一种基于XML的标记语言。它利用XML语法格式描述地理空间数据（如点、线、面、多边形和模型等），适合网络环境下的地理信息协作与共享。2008年4月，KML的版本2.2被开放地理信息联盟（Open Geospatial Consortium，OGC）宣布为开放地理信息编码标准，并改由OGC 维护和发展。现在很多GIS相关企业也采用此种格式进行地理数据的交换。

KML文件可以被Google Earth和Google Maps识别并显示。Google Earth和Google Maps处理KML文件的方式与网页浏览器处理HTML和XML文件的方式类似。像HTML一样，KML使用包含名称、属性的标签来确定显示方式。因此，可将Google Earth和Google Maps视为 KML文件浏览器。

既可以使用Google Earth创建KML文件，也可以使用XML或简单的文本编辑器从头输入“原始”KML。KML文件的语法与XML的语法基本相同，有以下几点需要注意的地方。

• KML文件的标签是大小写敏感的，且必须成对使用，必须正确嵌套。
• KML文件有两种基本的标签类型——单一标签和复合标签。复合标签的标签名首字母要大写，而单一标签都是小写的；复合标签能够作为其他标签（单一标签或复合标签）的父元素，而单一标签只能是其他复合标签的子元素，自身不能包含其他元素。
• KML文件只有一个根标签，可以使用、 、甚至 作为根标签。

beckley挑战题给出的remote.kml文件如下：

HackASatCompetition

0

0

HackASatComp1

View Centered Placemark

0

0

This is where the satellite was located when we saw it.

0

0

FILL ME IN          

FILL ME IN TOO        

FILL ME IN AS WELL     

FILL IN THIS VALUE        

FILL IN THIS VALUE TOO          

FILL IN THIS VALUE ALSO       

clampToGround

http://FILL ME IN:FILL ME IN/cgi-bin/HSCKML.py

1

onStop

1

BBOX=[bboxWest],[bboxSouth],[bboxEast],[bboxNorth];CAMERA= [lookatLon],

[lookatLat],[lookatRange],[lookatTilt],[lookatHeading];VIEW=[horizFov],[vertFov],[horizPixels],[vertPixels],[terrainEnabled]

为避免读者被太多信息干扰，本书只重点介绍在remote.kml文件中出现的元素及其子元素、的含义和用法，这也是解答beckley挑战题需要用到的背景知识。

1）元素

用于引用本地或远程服务器上的KML文件。可使用指定KML文件的位置。

2）元素

用于定义一个虚拟相机，指定地球上正被查看的景点（对于本题，读者可以将景点理解为华盛顿纪念碑）与视点（对于本题，读者可以将视点理解为卫星）间的距离及视图的角度。该元素的语法如下：

                    

                         

0                         

                                

0                                  

0                           

clampToGround

图2-5展示了KML文件中对视点的构建方式。

 

图2-5  KML文件中对视点的构建方式

、、、分别指出了被查看的景点的经度、纬度、高度和高度模式的值。指定-180°～180°的经度值；指定-90°～90°的纬度值；指定景点高出地平面、海平面或海底的高度值，其单位为m。通常，都会随附一个，该元素可告知Google Earth如何解析高度值。的取值如下：

• relativeToGround：表示从地球表面测量。
• absolute：表示从海平面上方测量。
• relativeToSeaFloor：表示从主水体的底部测量。
• clampToGround和clampToSeaFloor：表示高度可忽略。clampToGround模式会忽略所有高度值，并将KML地图项沿地形放置在地面上。在默认情况下，所有未指定高度模式的KML地图项都将使用clampToGround模式。

指出了视点到景点的距离，其单位为m。

指出了视点到景点的连线与景点处法线的夹角，其取值范围为[0°，90°]，0°表示视点从正上方看景点，90°表示视点沿水平线看景点。

指出了视图方向是否是北面朝上，若是北面朝上，则使用默认值0°；若不是，则指定一个0°（不含）到360°的旋转值，如图2-6所示。

图2-6  元素的含义图解

3）元素

当的父元素是时，用于指定KML文件的位置。该元素的语法如下：

...                        

onChange

4  

never

4  

1    

BBOX=[bboxWest],[bboxSouth],[bboxEast],[bboxNorth]

...                

指定一个URL地址，当的父元素是时，为KML文件的URL地址。

指定一种基于时间的刷新模式，可以是以下模式之一：

• onChange（默认值）：在加载文件和更改参数时刷新。
• onInterval：每n秒刷新一次（n在中指定）。
• onExpire：在达到过期时间时，将刷新该文件。
• 定义几秒钟刷新一次指定的文件。
• 定义当相机发生变化时，如何刷新，可取如下的值：
• never（默认值）：忽略视图的变化，同时忽略中的参数。
• onStop：在移动停止的n秒后刷新指定的文件，n由设置。
• onRequest：仅当用户明确请求时才刷新KML文件。
• onRegion：当Region变为active时刷新KML文件。

：设置当为onStop时，或者相机移动停止后，需等待几秒再刷新KML文件。

指定在获取KML文件时，附加在后面的查询用字符串格式。当的值为onStop，但KML文件不包含标签时，将自动附加下面的查询字符串：

BBOX=[bboxWest],[bboxSouth],[bboxEast],[bboxNorth]

若标签的值为空，则不会附加任何查询字符串。可以自定义查询字符串替换BBOX参数，或者自定义查询字符串和BBOX参数共存。

在自定义查询字符串中，可以组合使用下列参数：

• [lookatLon]、[lookatLat]：观测的景点的经纬度。
• [lookatRange]、[lookatTilt]、[lookatHeading]：使用的几个值，相关描述见的、、。
• [cameraLon]、[cameraLat]、[cameraAlt]：视点的坐标。
• [horizFov]、[vertFov]：视点的水平、垂直视场。
• [horizPixels]、[vertPixels]：3D视图的像素尺寸。
• [terrainEnabled]：指定3D视图是否显示地形起伏。

指定在将BBOX参数发送到服务器前如何对其进行缩放。小于1的值表示使用小于完整视图（屏幕）的值；大于1的值表示提取超出当前视图边缘的区域。

了解了KML文件格式，再回头观察主办方提供的remote.kml文件（前文已给出全部内容），可以看出，该文件中有8处标注“FILL IN”的位置，需要参赛者根据题目要求在这些位置处输入正确的参数值。前6处是要在内填写子标签、、、、和的参数值，从而将卫星拍照的位置定义为视点，将华盛顿纪念碑作为景点。后2处是要在的子标签中填写主办方所给出的服务器IP地址和端口号。

3．Python的Skyfield库

Skyfield是一个用于计算恒星、行星和在轨卫星位置的天文学Python库，其计算结果与美国海军天文台及其天文年历一致，误差在0.0005角秒以内。Skyfield用纯Python编写，无须任何编译即可安装，支持Python 2.6、Python 2.7和Python 3。Skyfield唯一的二进制依赖项是NumPy，NumPy是使用Python进行科学计算的一个基本包，它提供的矢量计算功能使Skyfield更加高效。

Skyfield的EarthSatellite对象能够从TLE文件中加载卫星轨道元素，并通过SGP4轨道模型算法来预测地球卫星的位置。需要注意每组TLE轨道根数的epoch点（这组轨道参数最准确的时间点），因为预测仅在epoch点前后一两周内有效。对于以后的日期，需要下载一组新的TLE轨道根数来预测，而对于较早的日期，需要从存档中提取一组旧的TLE轨道根数来预测。

查询某一时刻卫星在地心天球参考系中x、y、z坐标的代码如下：

from skyfield.api import EarthSatellite

from skyfield.api import load

ts = load.timescale()

line1 = '1 25544U 98067A   14020.93268519  .00009878  00000-0  18200-3 0  5082'

line2 = '2 25544  51.6498 109.4756 0003572  55.9686 274.8005 15.49815350868473'

#从TLE数据中加载卫星轨道元素

satellite = EarthSatellite(line1, line2, 'ISS (ZARYA)', ts)

print(satellite)

t = ts.utc(2014, 1, 23, 11, 18, 7)

geocentric = satellite.at(t)

print(geocentric.position.km)

运行输出结果如下：

ISS (ZARYA) catalog #25544 epoch 2014-01-20 22:23:04 UTC

[-3918.87650458 -1887.64838745  5209.08801512]

如果想查询在某一时刻，从地面上的观察者位置来看，这颗卫星是在地平线上方还是下方及从哪个方向寻找它，可以先构建一个Topos对象来表示观察者的纬度和经度，然后使用矢量减法来确定卫星相对于观察者的位置。

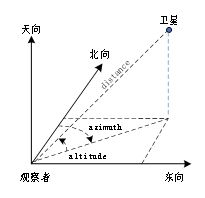
如图2-7所示，以观察者为中心建立坐标系，3个坐标轴分别指向相互垂直的东向、北向和天向，可以计算出卫星在此坐标系中的高度角altitude和方位角azimuth及卫星到观察者的距离distance。高度角从地平线的0°到天顶正上方的90°，负高度角表示卫星在观察者所在地平线以下。方位角是围绕地平线顺时针测量的，就像指南针上显示的度数一样，从地理上的北（0°）到东（90°）、南（180°）和西（270°），然后返回北，从359°回到0°。

图2-7  卫星在观察者坐标系中的表示

具体实现代码如下：

from skyfield.api import Topos

bluffton = Topos('38.8894838 N', '77.0352791 W')

difference = satellite - bluffton

topocentric = difference.at(t)

alt, az, distance = topocentric.altaz()

题目解析

这道题目其实就是让参赛者在Google Earth中利用KML文件模拟卫星的拍摄角度。具体而言，就是将卫星拍照的位置作为视点，将华盛顿纪念碑作为景点，在KML文件的中定义一个虚拟相机，关键是计算出、、、、和的值。

、表示景点的经纬度，填入华盛顿纪念碑的经纬度值即可；因为所给KML文件中的值为clampToGround，表示忽略高度，所以的值为0。只有、和的值需要计算。

这道题目提供了拍照卫星的TLE和拍照时间，可以利用这些数据通过Skyfield计算出给出的特定时刻，以及卫星相对于华盛顿纪念碑的高度角altitude、方位角azimuth和卫星到观察者的距离distance。

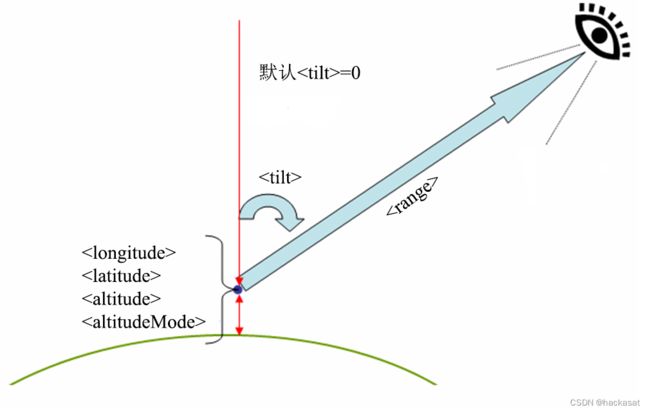
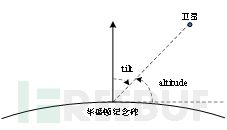
其中，表示视点到景点的连线与景点处法线的夹角，值与高度角altitude的关系如图2-8所示，所以其值为90°减去altitude的值。

图2-8  tilt角与altitude角的关系

表示的角度与方位角azimuth表示的角度正好相差180°，也可通过换算求得。

具体实现代码如下：

from skyfield.api import EarthSatellite

from skyfield.api import load

from skyfield.api import Topos

ts = load.timescale()

line1 = '1 13337U 98067A   20087.38052801 -.00000452  00000-0  00000+0 0  9995'

line2 = '2 13337  51.6460  33.2488 0005270  61.9928  83.3154 15.48919755219337'

satellite = EarthSatellite(line1, line2, 'REDACT', ts)

# EarthSatellite是一个Skyfield向量函数，使用SGP4简化模式模型，可以调用EarthSatellite的

# at()方法来生成卫星在天空中的位置，也可以使用加减法来与其他向量组合

# ts是一个时间刻度对象，用于生成epoch值

t = ts.utc(2020, 3, 26, 21, 52, 55)

photo = Topos('38.8894838 N', '77.0352791 W')

difference = satellite - photo

topocentric = difference.at(t)

alt, az, distance = topocentric.altaz()

print('Altitude(deg): %f' % alt.degrees)

print('Azimuth(def): %f' % az.degrees)

print('Range(m): %d' % int(distance.m))

tilt = 90 - alt.degrees

print('Tilt(deg): %f' % tilt)

heading = (180 + az.degrees) % 360

print('Heading(deg): %f' % heading)

运行上述代码，程序输出如下所示：

Altitude(deg): 40.033412

Azimuth(def): 240.186614

Range(m): 625347

Tilt(deg): 49.966588

Heading(deg): 60.186614

更新remote.kml文件，其应为：

-77.0352791

38.8894838

0

60.186614

49.966588

625347

clampToGround

将主办方所给出的服务器IP地址和端口号写入remote.kml文件的中，打开Google Earth Pro客户端软件，导入更新后的remote.kml文件，获得一个名为CLICK FOR FLAG的地标，如图2-9所示。

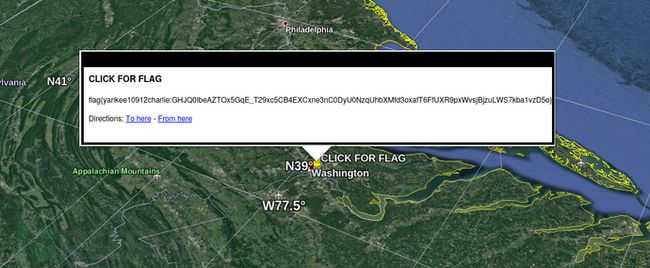
 图2-9 Google Earth Pro客户端软件导入KML文件后的界面

单击CLICK FOR FLAG地标，最终获取到flag值，如图2-10所示。

图2-10  beckley挑战题通过Google Earth Pro客户端获取到的flag